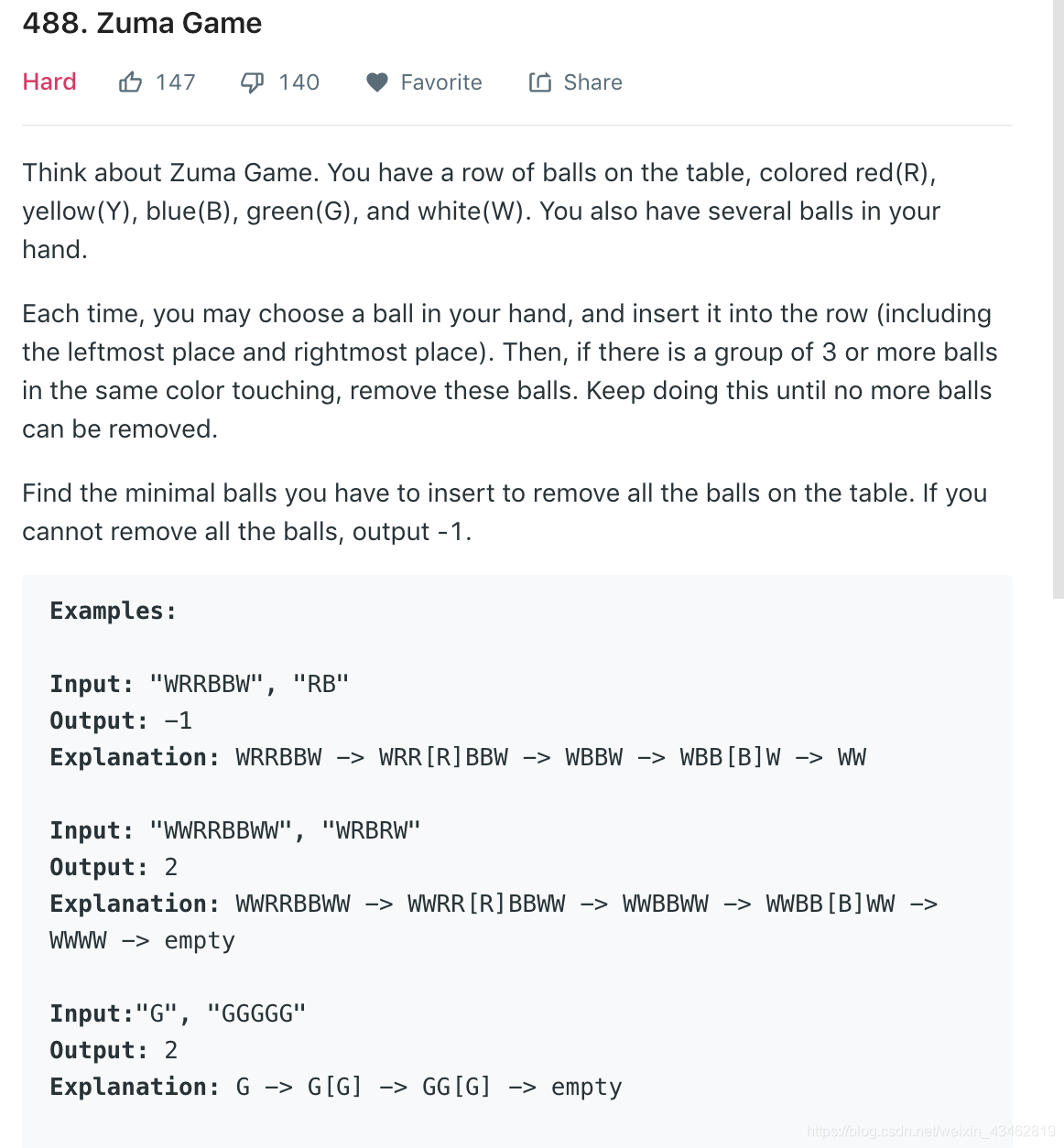
LeetCode：488. Zuma Game

先夸一下自己，终于不是看到难题就略过了，而是相信自己与之一战了（yeah

自己一开始想的是dp，但是就是写不出来。
然后看了评论区，说用回溯，而且这里的回溯给了我比较大的启发：

class Solution {
public:
    int findMinStep(string board, string hand) {
        vector<int> handCount(26, 0);
        for (char c : hand)
            handCount[c-'A']++;
        int ret = helper(board, handCount);
        return ret == 6? -1 : ret;
    }
private:
    int helper(string board, vector<int>& handCount) {
        board = removeBalls(board);//先进行消除
        if (board.empty())//再判断为不为空。因为有可能就是一个可以消除的串
            return 0;
        int i = 0, j = 0;
        int ret = 6;
        int sz = board.size();
        while (j < sz) {
            if (board[i] == board[j]) {
                ++j;
                continue;
            }
            int need = 3 - (j - i);
            assert(need < 3);
            if (need <= handCount[board[i] - 'A']) {
                handCount[board[i]-'A'] -= need;
                ret = min(ret, need + helper(board.substr(0, i) + board.substr(j, sz-j), handCount));
                handCount[board[i]-'A'] += need;
            }
            i = j;
        }
        int need = 3 - (j - i);
        assert(need < 3);
        if (need <= handCount[board[i] - 'A']) {
            handCount[board[i]-'A'] -= need;
            ret = min(ret, need + helper(board.substr(0, i), handCount));
            handCount[board[i]-'A'] += need;
        }
        return ret;
    }
    
    
    string removeBalls(string board) {
        if (board.size() < 3)
            return board;
        int sz = board.size();
        int i = 0, j = 0;
        while (j < sz) {
            if (board[i] == board[j]) {
                ++j;
                continue;
            }
            if (j - i >= 3) {
                return removeBalls(board.substr(0, i) + board.substr(j, sz-j));
            } else
                i = j;
        }
        if (j - i >= 3)//可能最后一段是符合的
            return removeBalls(board.substr(0, i));
        return board;
    }
};
//这里回溯的方法就是：
//每次看一段连续的球，看看如果把它消掉，产生的结果会是多少？也就是实验所有可能。这应该是回溯的根本思想。

//还有比较有意思的点是：关于处理可能一段球消掉产生的新的连接处又可以消的情况：使用递归

这里对于我来说最难想出来的就是如何回溯：
之前自己做的回溯的题目一般是一个字符串，或者一个二维数组，在里面试探性地进行摸索。但是回溯的根本思想（在我看来）就是实验所有的可能性。这个题目给了新的思路。

难的题目往往是由几个稍微难的小问题组成的：比如这里最后一个函数解决的就是“给一个string，消除其中连续出现字符3次及以上的子串”。如果一想到要解决这么多的小问题就胆怯的话，恐怕自己解决hard问题的一天不会到来。
所以解决比较难的题目的时候，将大问题分解出来，清晰地定义出小问题，一个一个解决，就行了。

另外，这题给我的启示是：
回溯是万能解法。其他方法不行（dp之类的），就可以考虑回溯（尝试所有方法）了。（虽然很可能超时）