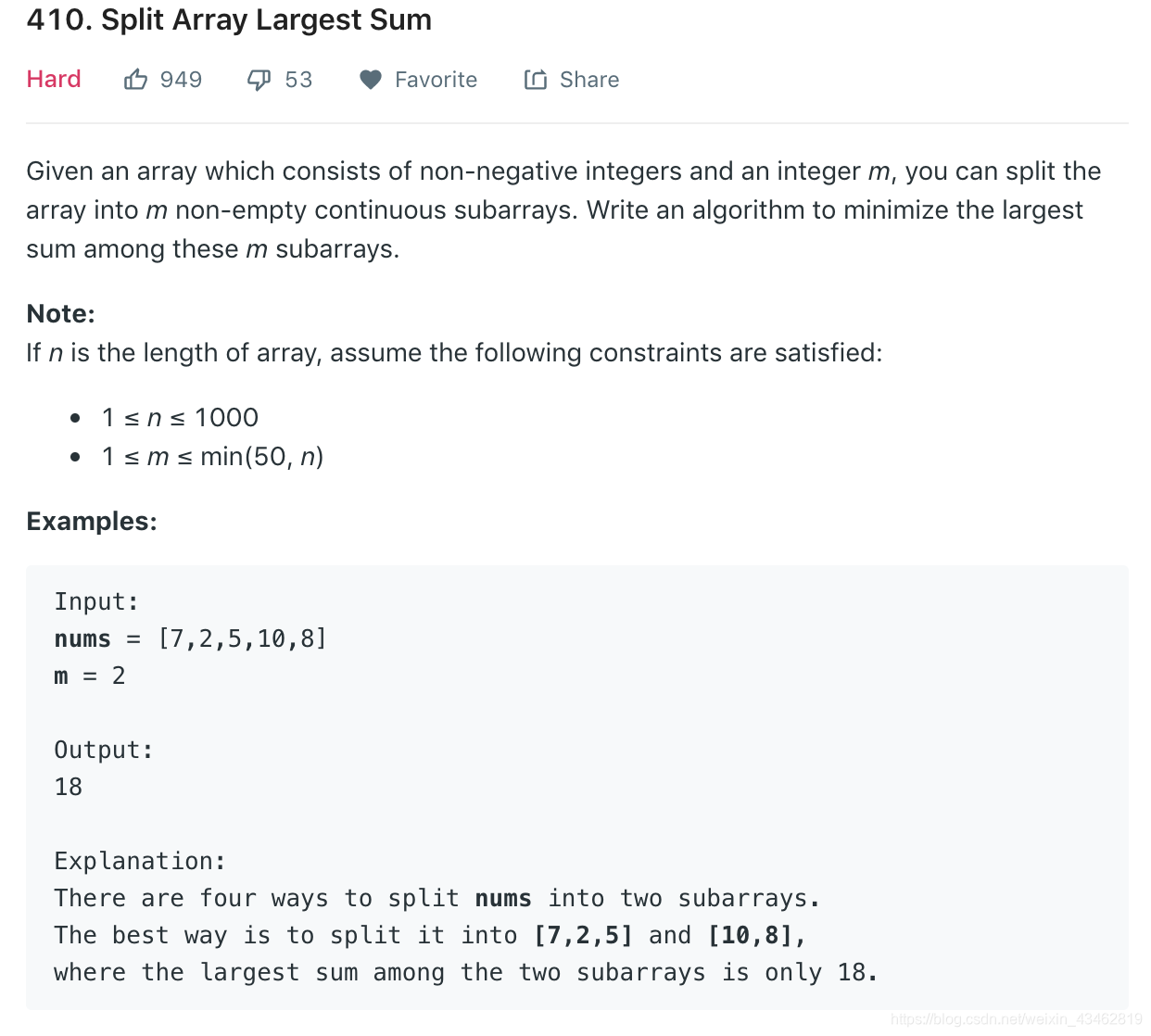
LeetCode：410. Split Array Largest Sum

两种方法：二分和dp
1.
又是一道二分查找。不要想复杂了的典范。

再引用一次前面博文的总结归纳：
https://blog.csdn.net/weixin_43462819/article/details/90903807
不太容易看出二分的题目，应该都是取值有明确的上下限，最终的结果是一个值，然后这个值的一边行，另一边不行，要我们求到这个值。应该可以想到是二分法。
这是很重要的一点——“一边可以，另一边不可以，有明确的分界线”，几乎没有其他问题符合这个条件。符合这个条件的，二分往往是最好的解决方法，因为logn
这一题完美符合。

可能想不到的关键点在于：“行不行”在这一类题目中不是这么容易看出来，而不是像最简单的二分搜索中使用==就可以判断出来。比如之前的吃香蕉的题目，行不行需要单独写个函数判断；类似这一题，当前这个“最小的最大和”行不行，也是需要一个单独判断的函数（难问题都是由小问题组成的）

如果有感觉某一题可以这么做，这么思考：
1.找上下界
2.是一边可以，另一边不可以吗
3.考虑如何判断可不可以

再说一句，也不一定是一边行，另一边不行。也可以只有一个数可以，但是要有明确的上下界，猜错了直到往哪边走。这样也是可以的。

之前博文连接：
https://blog.csdn.net/weixin_43462819/article/details/90903807

2.dp
这一道题目的状态应该是很容易想起来的：
先是想的：i->j，分成m个，最小的最大连续子串和为多少。
然后一想，都是要从头开始的，所以换为：0->i,分成m个，最小的最大连续子串和为多少？
转移方程是：对于0<=k<i，dp[i][m] = min(dp[i][m], max(dp[k-1][m-1], sum[k->i])), 0 <= k <= i.
先是top-down+memo:

class Solution {
public:
    int splitArray(vector<int>& nums, int m) {
        map<pair<int, int>, int> mpi;
        vector<int> maxEndHere(nums.size(), 0);
        maxEndHere[0] = nums[0];
        for (int i = 1; i < nums.size(); ++i)
            maxEndHere[i] = max(nums[i], maxEndHere[i-1]);
        return helper(nums, mpi, nums.size()-1, m, maxEndHere);
    }
private:
    int helper(vector<int>& nums, map<pair<int, int>, int>& mpi, int i, int m, vector<int>& maxEndHere) {
        if (i < 0)
            return 0;
        if (m == 0)
            return INT_MAX;
        if (m >= i+1)
            return maxEndHere[i];
        auto p = make_pair(i, m);
        if (mpi.find(p) != mpi.end())
            return mpi[p];
        int sum = 0;
        int val = INT_MAX;
        for (int k = i; k >= 0; --k) {
            sum += nums[k];
            if (sum > val) {
                mpi[p] = val;
                return val;
            }
            val = min(val, max(helper(nums, mpi, k-1, m-1, maxEndHere), sum));
        }
        mpi[p] = val;
        return val;
    }
};

然后是bottom-up

暂时没有写出来

需要说的是：
这一题的状态是：0->i,分成j段，最小的最大子串和是多少。
可以看出：状态的定义往往是：一个“子问题”，也就是说原来是0->sz, 分成m段；这里状态定义了小的，但是“条件是都有的”。目的是“最小的最大子串和是多少“，这是和题目要求吻合的，在其他一些题目中为了状态转移方程的书写，可能需要定义不同的目的。

再回想一下之前的题目，比如：
比如：can i win里面，子状态是在留有一些数的情况下（和题目相同，不过更小），第一个动手的人能不能赢。条件相同（小一些），目的也相同。(注意我们的目的是算出能不能赢，而不是达到target，那是玩游戏的人的目的）
再比如：stone game1中，子状态是：先从i-j中挑的人能赢过对手的最大数目。条件相同，但是目的不同，为了写转移方程。目的不同，最后需要转换一下才能得到最终的答案。

所以说，状态的定义应该是：
给出和题目相同的条件（不过是更小一些的），然后求这个条件下和题目相同或者不同的目的。

这应该是做dp难题目最大的启发点了。