768. Max Chunks To Make Sorted II

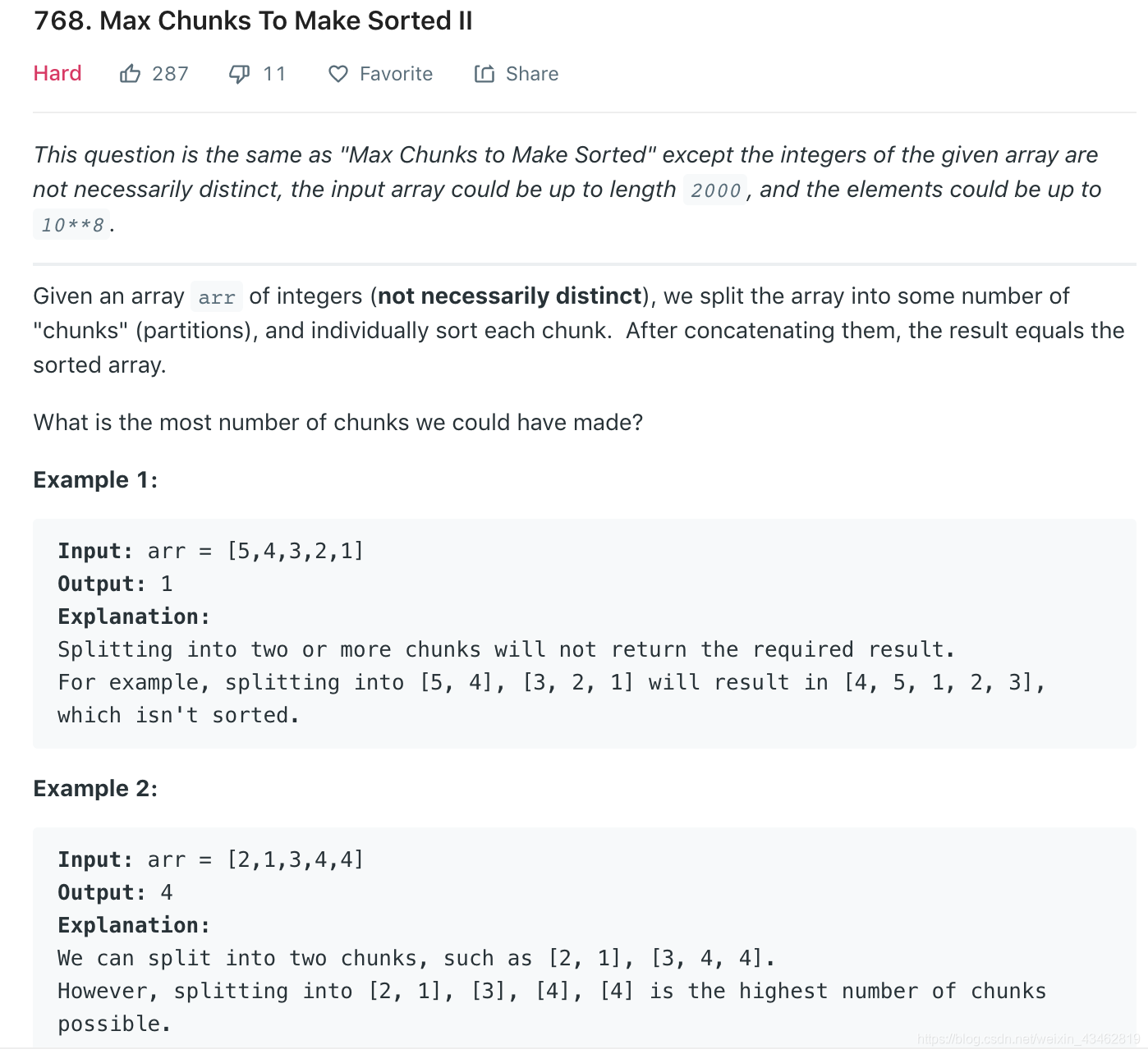
为数不多的能够自己较快的做出的hard题目，可喜可贺（虽然是在第一题的基础上来的，而且方法不是最优）。

方法一：
自己的方法。
把每个数字应该在的位置都算出来。然后每次从一个位置出发去到目标位置，图中如果有更大的目标位置，就更新它，直到到达。这算一个chunk
对于相等数字的处理：对于它们的位置初始保存了第一个位置，然后每用一次位置加一。

class Solution {
public:
    int maxChunksToSorted(vector<int>& arr) {
        int sz = arr.size();
        vector<int> dup(arr.begin(), arr.end());
        sort(dup.begin(), dup.end());
        unordered_map<int, int> m;
        for (int i = 0; i < sz; ++i) {
            if (i > 0 && dup[i] == dup[i-1])
                continue;
            m[dup[i]] = i;
        }
        //for (auto item : m)
            //cout << item.first << " " << item.second << endl;
        int retCnt = 0;
        int i = 0;
        int maxReach = -1;
        while (i < sz) {
            while (i < sz) {
                maxReach = max(maxReach, m[arr[i]]++);
                if (i == maxReach)
                    break;
                ++i;
            }
            ++i;
            ++retCnt;
        }
        return retCnt;
    }
};

方法二：
这就需要敏锐的洞察力了。
观察每个位置：如果这个位置左边的所有数都要小于右边的所有数，那么就算一个chunk。
即到当前位置左边的最大值小于右边的最小值，算一个chunk。

class Solution {
public:
    int maxChunksToSorted(vector<int>& arr) {
        int sz = arr.size();
        vector<int> maxFromLeft(sz), minFromRight(sz);
        maxFromLeft[0] = arr[0];
        for (int i = 1; i < sz; ++i)
            maxFromLeft[i] = max(maxFromLeft[i-1], arr[i]);
        minFromRight[sz-1] = arr[sz-1];
        for (int i = sz-2; i >= 0; --i)
            minFromRight[i] = min(minFromRight[i+1], arr[i]);
        int retCnt = 0;
        for (int i = 0; i < sz-1; ++i)
            if (maxFromLeft[i] <= minFromRight[i+1])
                ++retCnt;
        return retCnt+1;
    }
};

最后的+1是因为最后一块chunk没有算上。
然后可以优化内存到只用一个数组（比如只要minFromRight），然后迭代的过程中位置maxHere。

记得之前做过这种需要maxFromLeft或者minFromRight的题目。可以用来解决左边所有值小于（大于）右边值的问题。因为还可以拓展到其他类型的题目上，可以注意之后总结一下。

方法三：
真正牛逼的方法。

class Solution {
public:
    int maxChunksToSorted(vector<int>& arr) {
        vector<int> dup(arr);
        sort(dup.begin(), dup.end());
        long long sum1 = 0, sum2 = 0;
        int retCnt = 0;
        for (int i = 0; i < arr.size(); ++i) {
            sum1 += arr[i];
            sum2 += dup[i];
            if (sum1 == sum2)
                ++retCnt;
        }
        return retCnt;
    }
};

到目前的最小值的和如果与arr的和相等，那么说明arr之前的数也是相应的最小值，所以是可以的。
OrZ