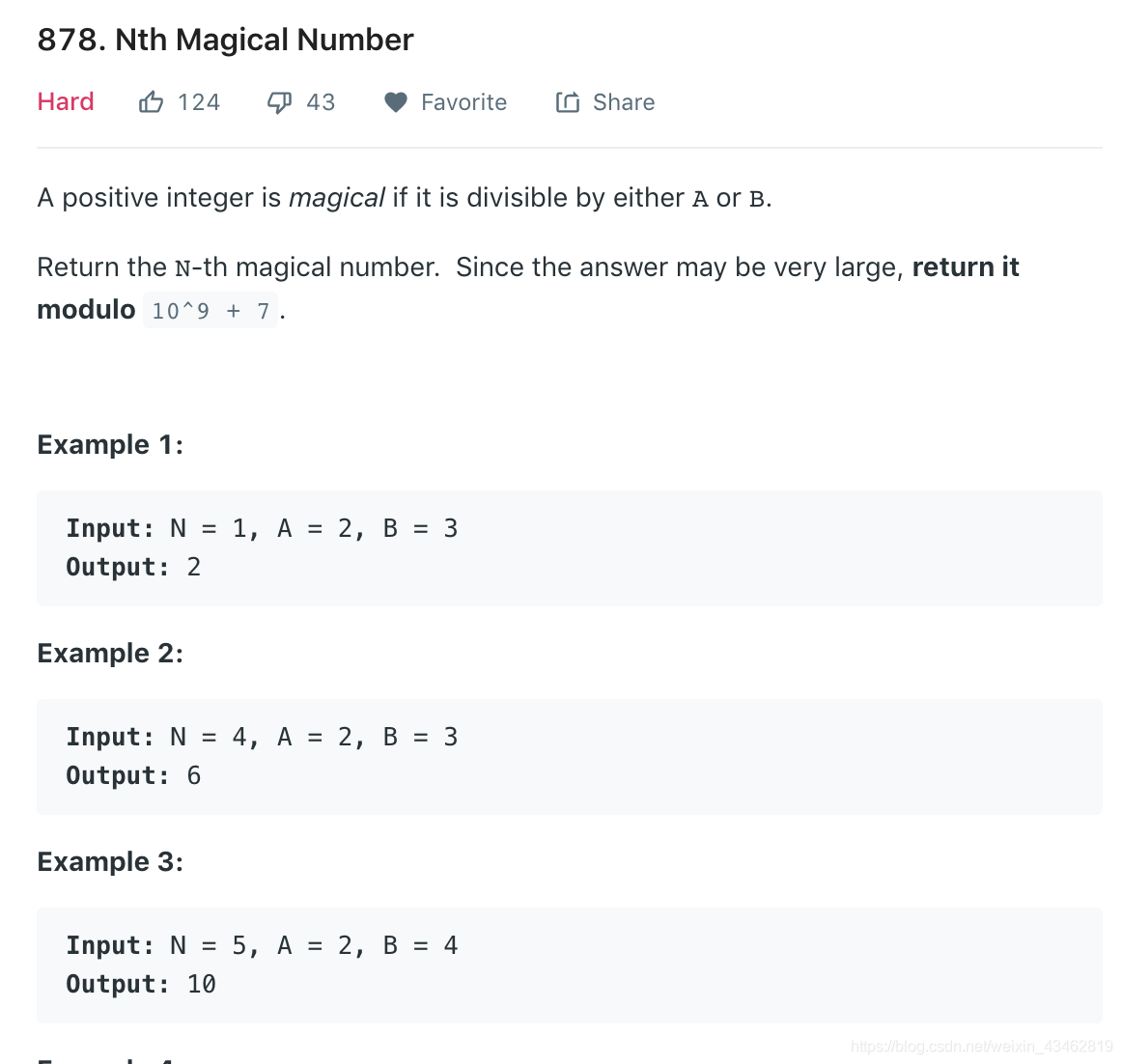
878. Nth Magical Number

虽然也不指望自己能够做出来这道题，但是解答的过程中包含的知识点不少，有些以后或许可以用得上。

1） lcm (least common multiple)，也就是两个数的最小公倍数。怎么算：A*B/gcd，gcd是最大公约数（用辗转相除法）
2）对于<=x，有多少magic numbers？
x/A + x/B - x/lcm
A的倍数有多少个+B的倍数有多少个-最小公倍数的倍数有多少个（是被重复计算的）
这么一看确实很明显，但是真要自己想不一定想的出来。
3）设置二分搜索时，如果上下限不是那么好确定，那么可以设的宽一些，不碍事的，或者直接接近int的上下限（logn的复杂度决定了这不是问题）
4）目的是找到x / A + x / B - x / lcm = N的最小值。整个区间中，应该是这样：
<N || ==N || >N
其中有等于号是因为有一段不是整除导致结果也等于N，所以我们要找最小的。所以这种找一个分界值的问题可以用二分。

所以总的来说，这道题最难的是把：<=x中有x/A + x/B - x/lcm个magic number这个公式算出来。也算开眼了。

class Solution {
public:
    int nthMagicalNumber(int N, int A, int B) {
        long long lcm = A*B/__gcd(A, B), l = 2, r = 1e14, mod = 1e9+7;
        while (l < r) {
            long long m = (l+r)/2;
            if (m/A + m/B - m/lcm < N) l = m+1;
            else r = m;
        }
        return l%mod;
    }
};

另外，最大公约数的证明：
a和b的最大公约数也是b和a%b的最大公约数。
假设a和b的最大公约数为r
那么a可以整除r，b也可以整除r。因为a % b = a - k * b，很容易知道，

（a - k * b）/ r = a / r - k * b / r 因此a%b 一定也可以整除r
所以：

int gcd(int a, int b)
{
  if( b==0 )return a;//上面那层递归实例的 b是这层的a b==0 说明上面一层的 a%b == 0了
  return gcd(b, a%b);
}

另外a<b也是可以的。