LintCode:背包问题
题目列表和解答:
https://blog.csdn.net/luoshengkim/article/details/76514558
关于背包问题的总结看最下面。
92. Backpack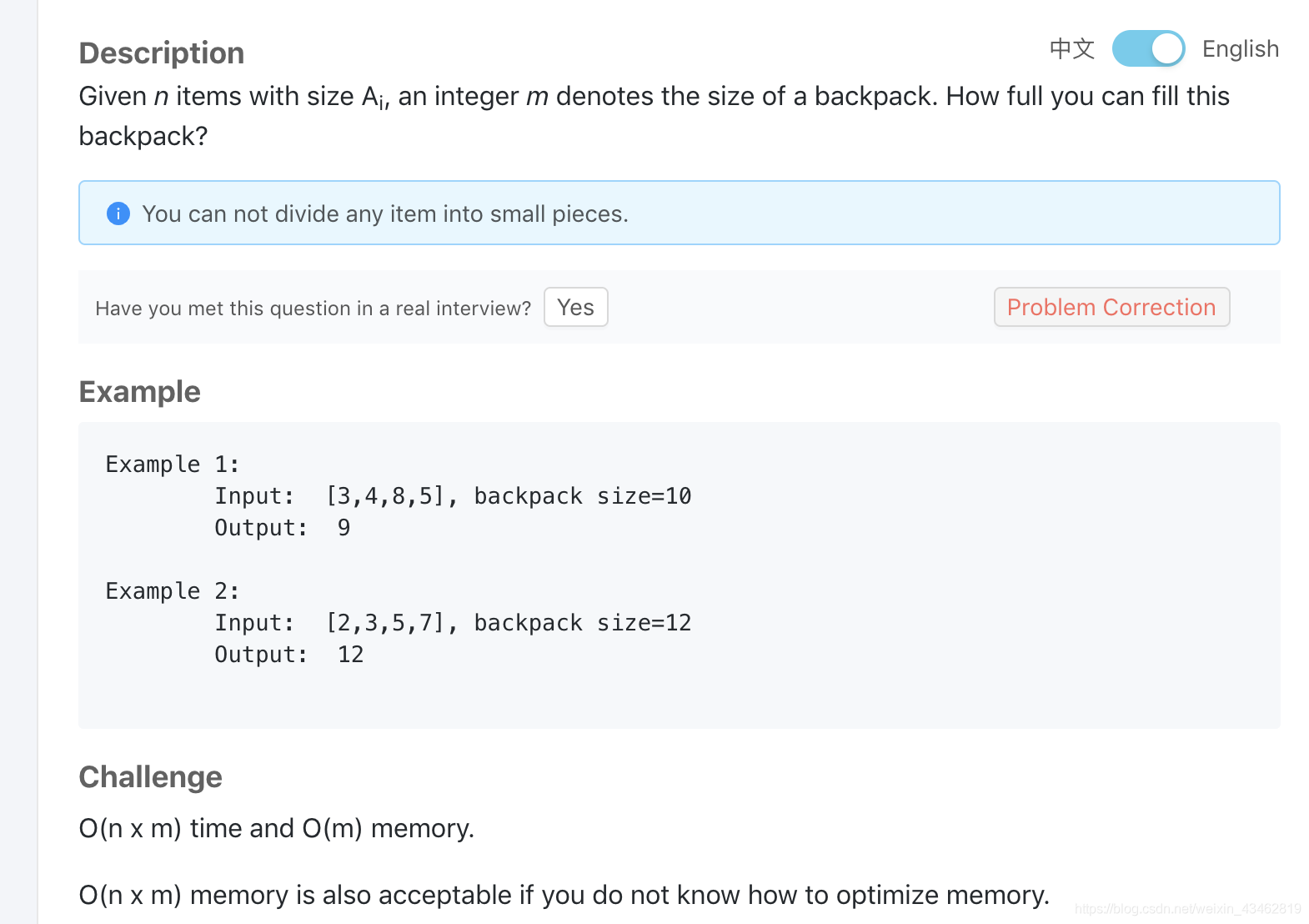
class Solution {
public:
/**
* @param m: An integer m denotes the size of a backpack
* @param A: Given n items with size A[i]
* @return: The maximum size
*/
int backPack(int m, vector<int> &A) {
int sz = A.size();
vector<vector<bool>> dp(sz+1, vector<bool>(m+1, false));
dp[0][0] = true;
for (int i = 1; i <= sz; ++i)
for (int j = 0; j <= m; ++j) {
if (A[i-1] > j)
dp[i][j] = dp[i-1][j];
else
dp[i][j] = dp[i-1][j-A[i-1]] || dp[i-1][j];
}
for (int i = m; i >= 0; --i)
if (dp[sz][i])
return i;
return 0;
}
};
- Backpack II
![在这里插入图片描述]()
class Solution {
public:
/**
* @param m: An integer m denotes the size of a backpack
* @param A: Given n items with size A[i]
* @param V: Given n items with value V[i]
* @return: The maximum value
*/
int backPackII(int m, vector<int> &A, vector<int> &V) {
// write your code here
int sz = A.size();
vector<vector<int>> dp(sz+1, vector<int>(m+1, 0));
for (int i = 1; i <= sz; ++i)
for (int j = 1; j <= m; ++j) {
if (A[i-1] > j)
dp[i][j] = dp[i-1][j];
else
dp[i][j] = max(dp[i-1][j-A[i-1]]+V[i-1], dp[i-1][j]);
}
return dp.back().back();
}
};
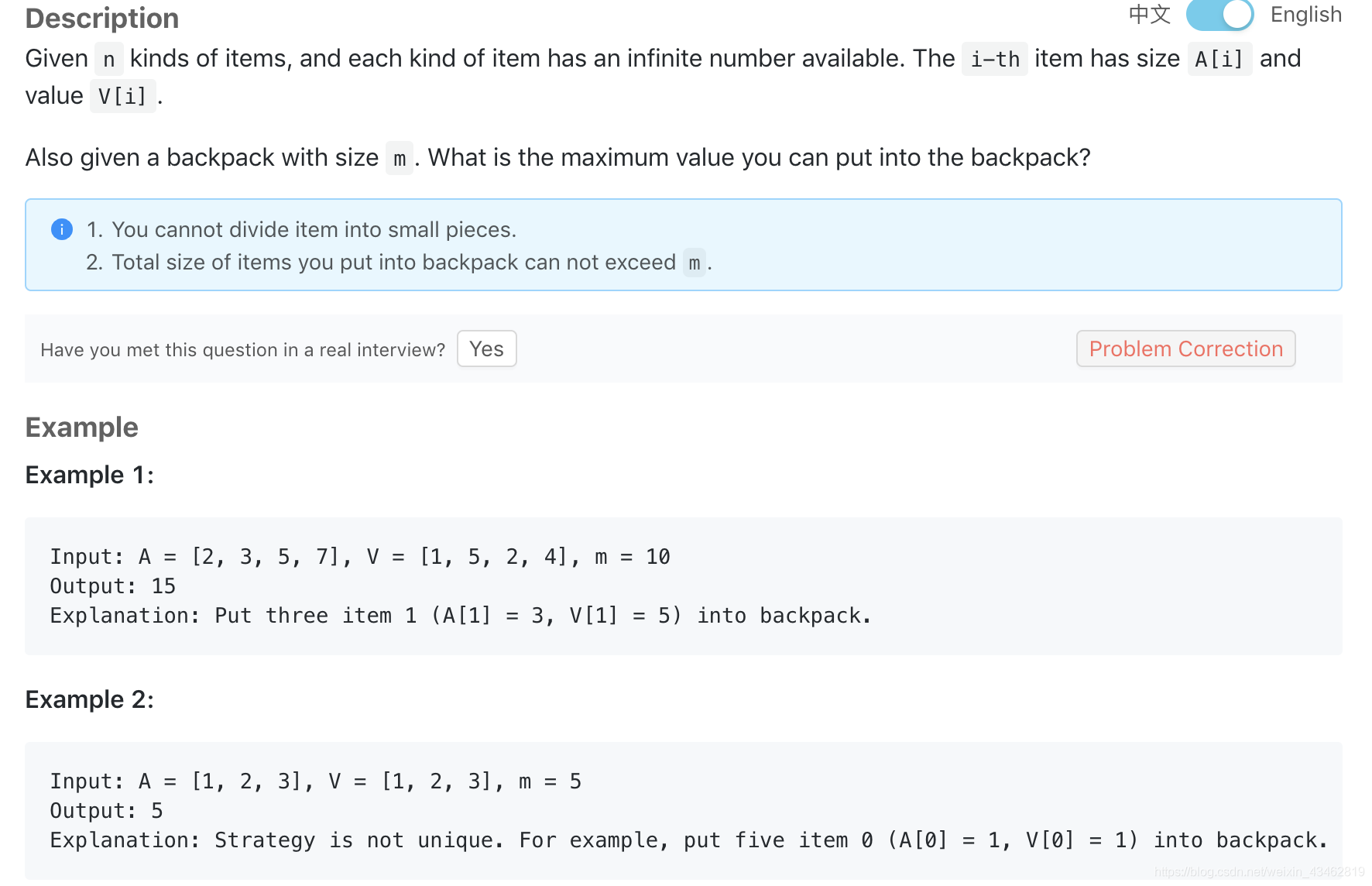
- Backpack III
![在这里插入图片描述]()
class Solution {
public:
/**
* @param A: an integer array
* @param V: an integer array
* @param m: An integer
* @return: an array
*/
int backPackIII(vector<int> &A, vector<int> &V, int m) {
// write your code here
int sz = A.size();
vector<vector<int>> dp(sz+1, vector<int>(m+1, 0));
for (int i = 1; i <= sz; ++i)
for (int j = 1; j <= m; ++j) {
int k = 0;
while (j >= A[i-1]*k) {
dp[i][j] = max(dp[i][j], dp[i-1][j-A[i-1]*k]+V[i-1]*k);
++k;
}
}
return dp.back().back();
}
};
- Backpack IV
class Solution {
public:
/**
* @param nums: an integer array and all positive numbers, no duplicates
* @param target: An integer
* @return: An integer
*/
int backPackIV(vector<int> &nums, int target) {
// write your code here
int sz = nums.size();
vector<vector<int>> dp(sz+1, vector<int>(target+1, 0));
for (int i = 0; i <= sz; ++i)
dp[i][0] = 1;
for (int i = 1; i <= sz; ++i)
for (int j = 1; j <= target; ++j) {
int k = 0;
while (j-nums[i-1]*k >= 0) {
dp[i][j] += dp[i-1][j-nums[i-1]*k];
++k;
}
}
return dp.back().back();
}
};
- Backpack V
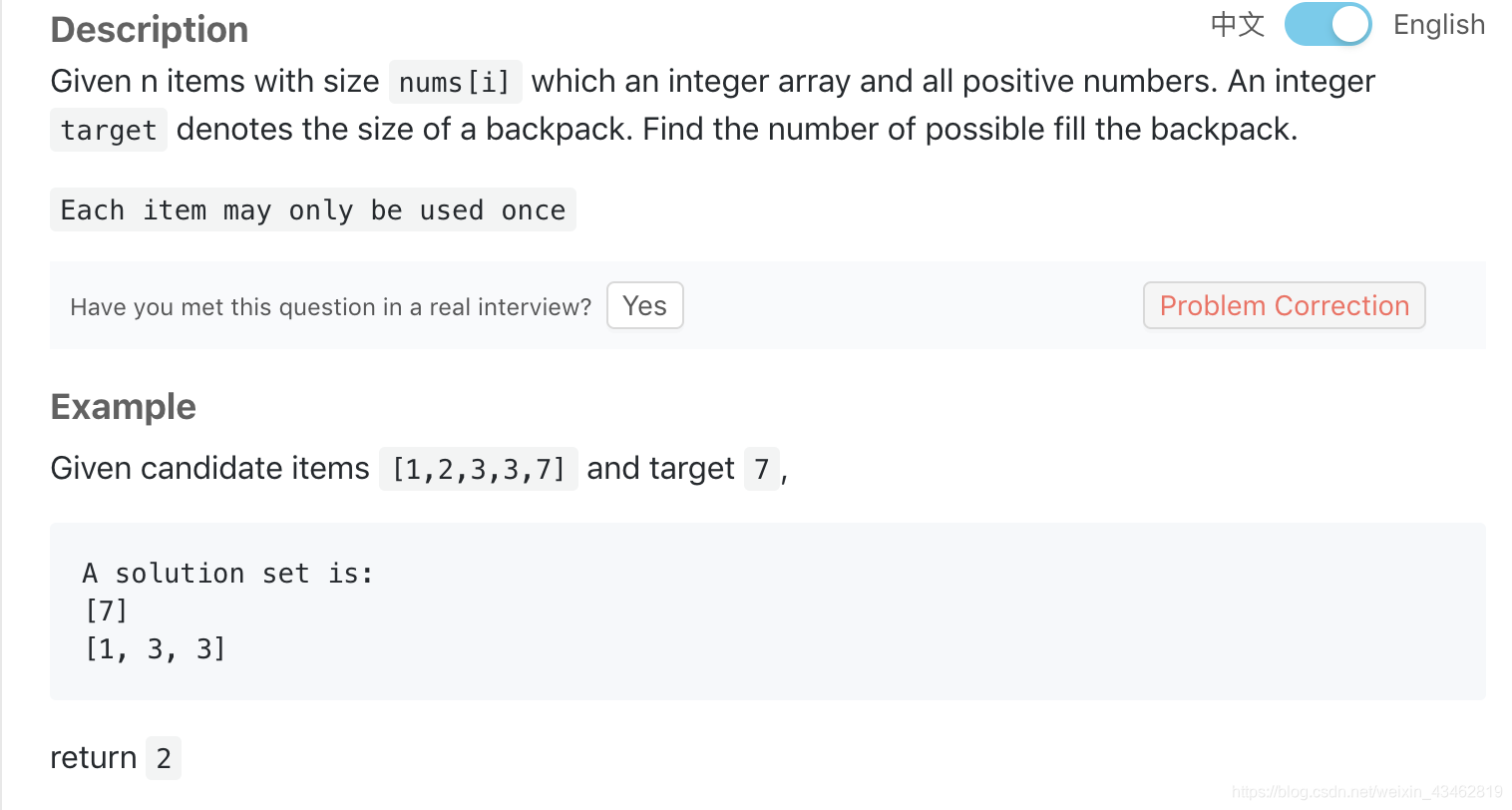
class Solution {
public:
/**
* @param nums: an integer array and all positive numbers
* @param target: An integer
* @return: An integer
*/
int backPackV(vector<int> &nums, int target) {
// write your code here
int sz = nums.size();
vector<vector<int>> dp(sz+1, vector<int>(target+1, 0));
for (int i = 0; i <= sz; ++i)
dp[i][0] = 1;
for (int i = 1; i <= sz; ++i)
for (int j = 1; j <= target; ++j) {
if (nums[i-1] > j)
dp[i][j] = dp[i-1][j];
else
dp[i][j] = dp[i-1][j] + dp[i-1][j-nums[i-1]];
}
return dp.back().back();
}
};
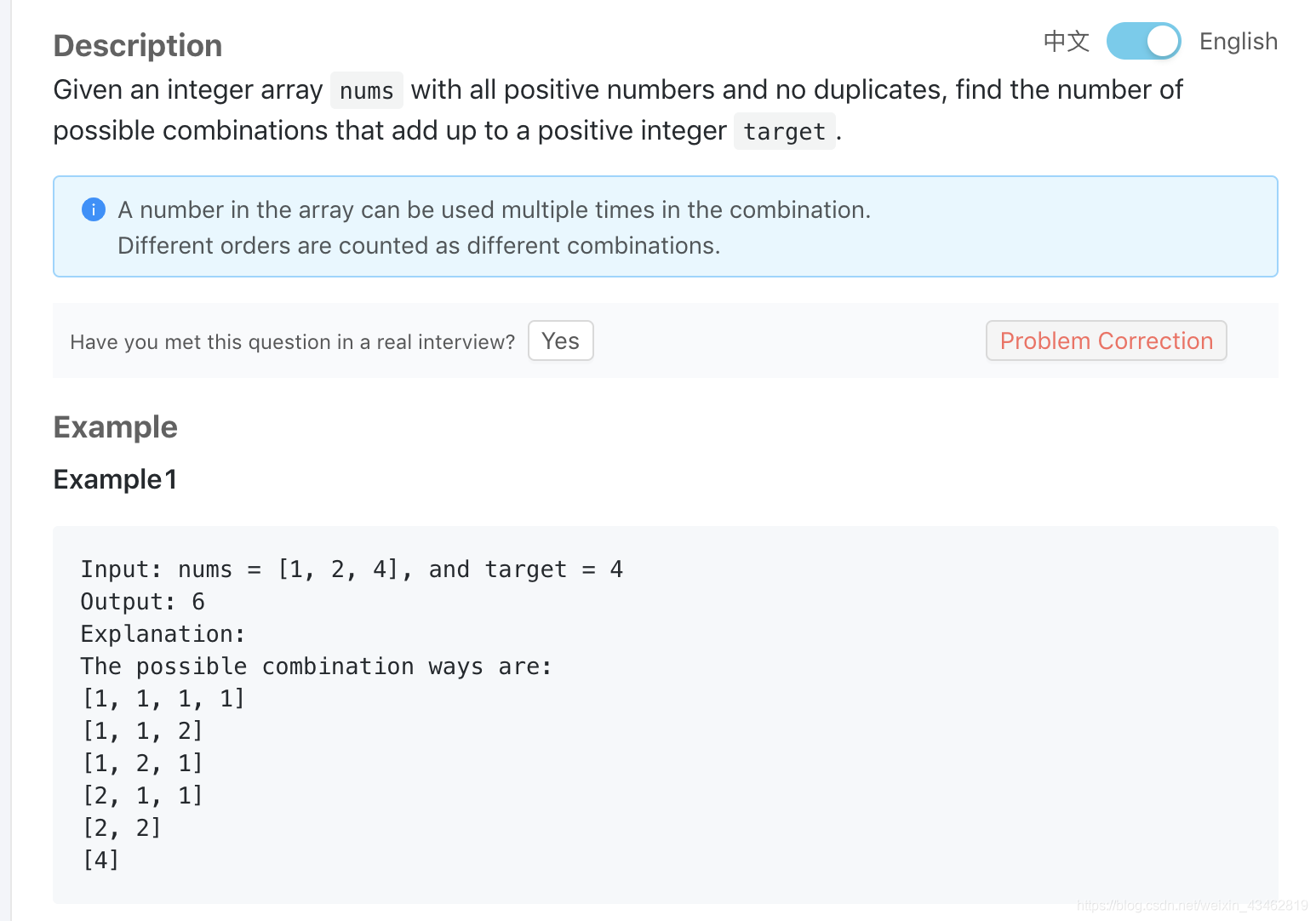
- Combination Sum IV
![在这里插入图片描述]()
class Solution {
public:
/**
* @param nums: an integer array and all positive numbers, no duplicates
* @param target: An integer
* @return: An integer
*/
int backPackVI(vector<int> &nums, int target) {
// write your code here
int sz = nums.size();
vector<int> dp(target+1, 0);
dp[0] = 1;
for (int i = 0; i <= target; ++i) {
for (int num : nums)
if (i >= num)
dp[i] += dp[i-num];
}
return dp.back();
}
};
注意这题自己没有做出来。
这里依然是把值作为dp的维度。但是因为不同顺序的作为不同的答案,所以没有限制前i个组成大小j。这里其他题目,不同顺序都是算相同的答案的,所以限制了“前i个”这一条件。
从后面开始思考这题会比较好。
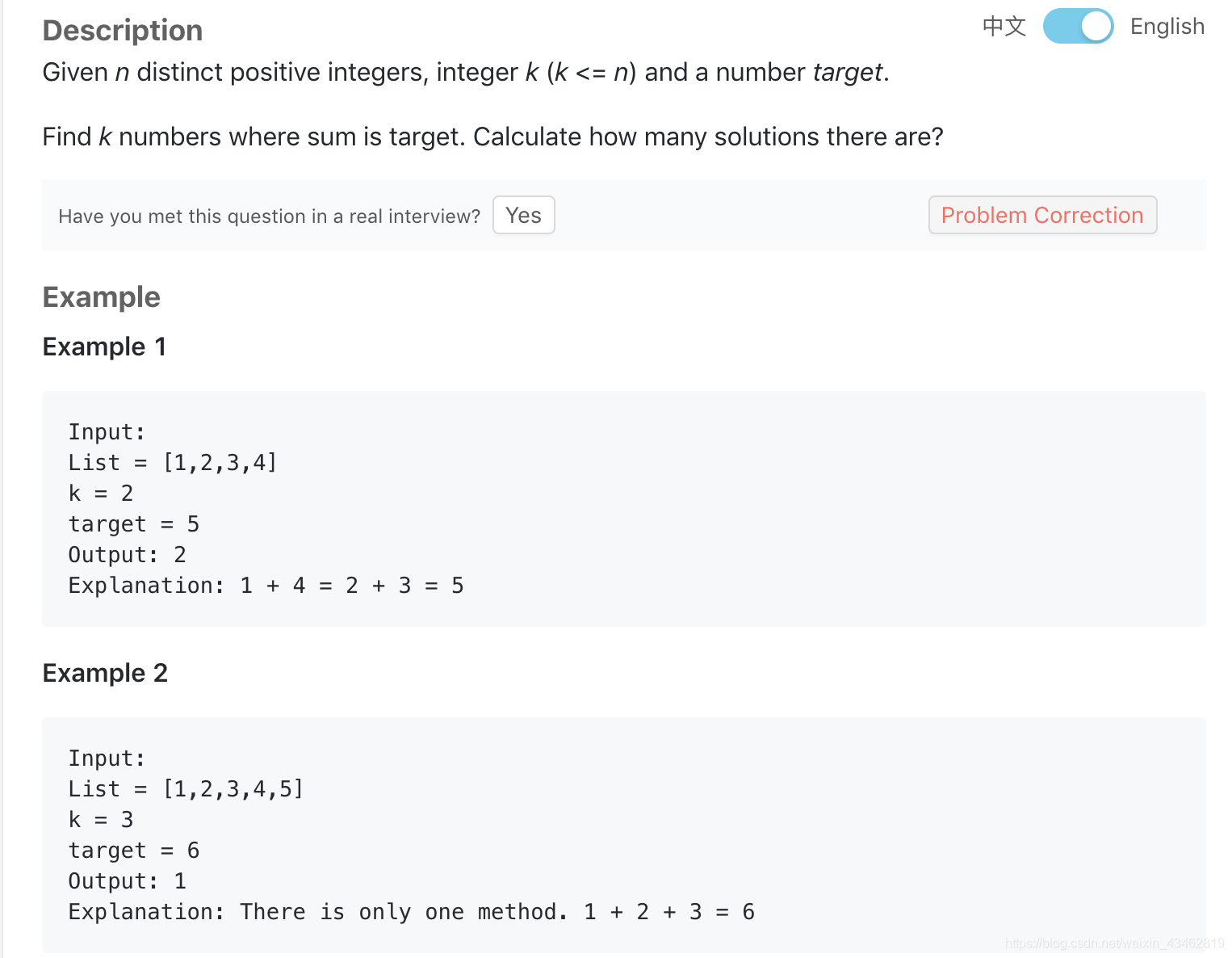
- k Sum
![在这里插入图片描述]()
class Solution {
public:
/**
* @param A: An integer array
* @param k: A positive integer (k <= length(A))
* @param target: An integer
* @return: An integera
*/
int kSum(vector<int> &A, int k, int target) {
// write your code here
int sz = A.size();
vector<vector<vector<int>>> dp(sz+1, vector<vector<int>>(k+1, vector<int>(target+1, 0)));
for (int i = 0; i <= sz; ++i)
dp[i][0][0] = 1;//注意这个初始条件。
for (int a = 1; a <= sz; ++a)
for (int b = 1; b <= k; ++b)
for (int c = 1; c <= target; ++c) {
if (A[a-1] > c)
dp[a][b][c] = dp[a-1][b][c];
else
dp[a][b][c] = dp[a-1][b][c] + dp[a-1][b-1][c-A[a-1]];
}
return dp.back().back().back();
}
};
这一题没有自己做出来,注意这一题。
还是把值作为维度,这一题有两个“值”的要求,一是k个,二是target,需要把它们都加到维度里面(另外顺序不同算相同答案,所以加限制“前i个”)。
所以来说,背包就是把所有可能值(条件给出的限制范围内)都取到,为了给后面的计算来使用。
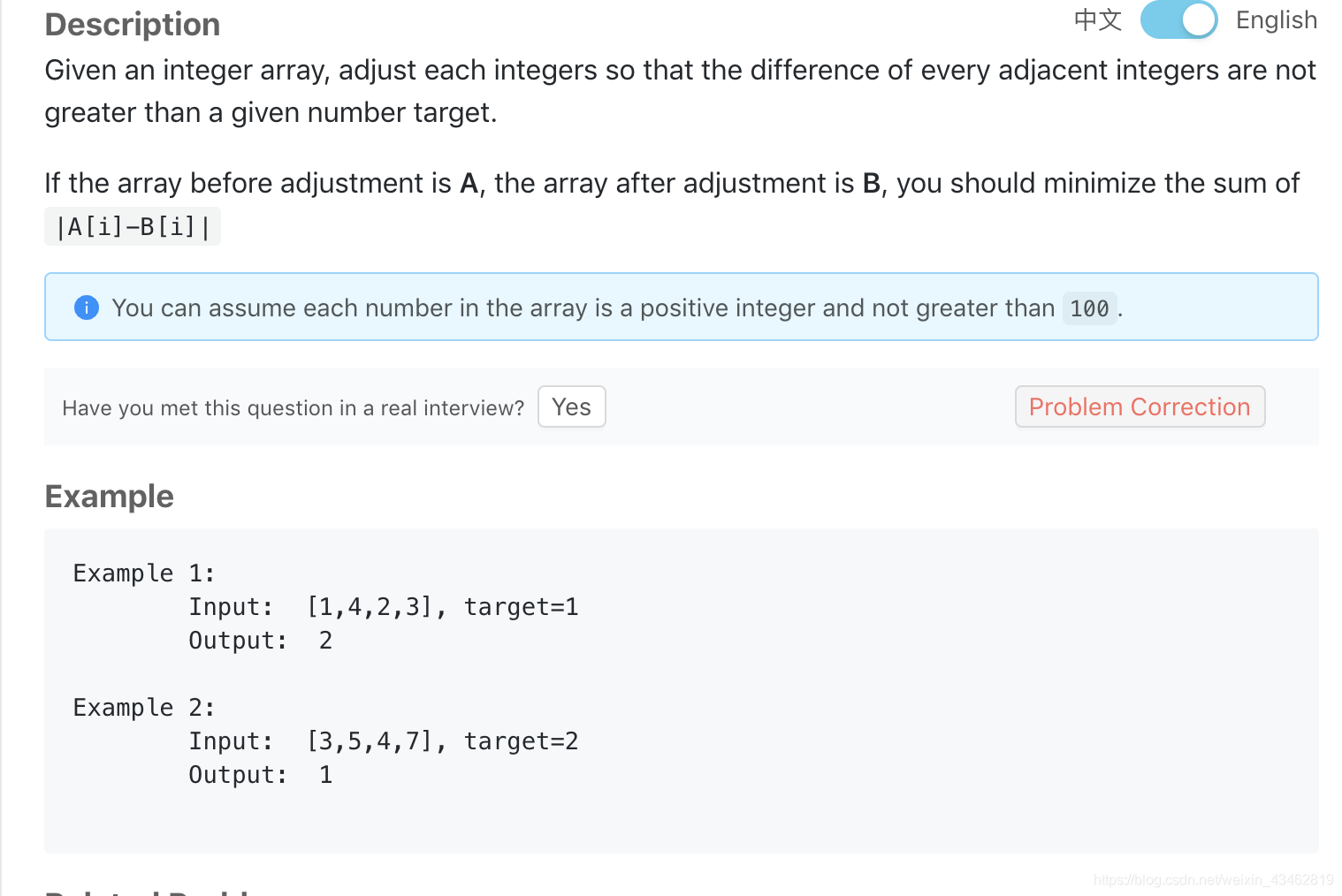
- Minimum Adjustment Cost
![在这里插入图片描述]()
这一题很有意思,保证下次自己再遇上还是不会做。
多注意一下。
class Solution {
public:
/*
* @param A: An integer array
* @param target: An integer
* @return: An integer
*/
int MinAdjustmentCost(vector<int> &A, int target) {
// write your code here
int sz = A.size();
vector<vector<int>> dp(sz+1, vector<int>(101, INT_MAX));
for (int j = 0; j <= 100; ++j)
dp[0][j] = 0;
for (int i = 1; i <= sz; ++i)
for (int j = 1; j <= 100; ++j) {
for (int v = 1; v <= 100; ++v)
if (abs(j-v) <= target)
dp[i][j] = min(dp[i][j], dp[i-1][v]+abs(j-A[i-1]));
}
int ret = INT_MAX;
for (int j = 1; j <= 100; ++j)
ret = min(ret, dp[sz][j]);
return ret;
}
};
这一题很有意思,把它放到背包问题里面因为它揭示了背包问题应该怎么做。就是把每一个可能取到的值都取到
这一题:对于前n个数,把它能够取到的每个值都取到试一试(而且确实它都应该可以取到)。然后迭代到后面的时候,想要前面的取到任何值,都可以取得相应结果。感觉这是背包的本质?算到后面位置的时候,确实需要前面取到每一个值时候的情况,那就把它们全部算出来。
对背包问题的总结:
背包特征:就是把所有可能值(条件给出的限制范围内)都取到,为了给后面的计算来使用。
要不要用背包:
1.如果可以从比当前条件小的条件的情况下推出当前条件的状态,可以考虑用背包。
2.如果一个问题就是讨论对于一组元素,对于每一个讨论要不要它,就可以考虑用背包,之前博文里面讨论的
怎么用背包:
1.总有一维(或者多维)是给出的限制条件的值(所以往往需要限制条件的范围是明确的)
2.然后按照情况,看看需不需要加上限制“对于前i个”,这好像没有统一的方式来判断。
其实相对于普通dp来说,https://blog.csdn.net/weixin_43462819/article/details/100023283
背包也没有什么特殊的地方,都是给出比题目比较小的条件。
用类似的思路做:
800. Backpack IX
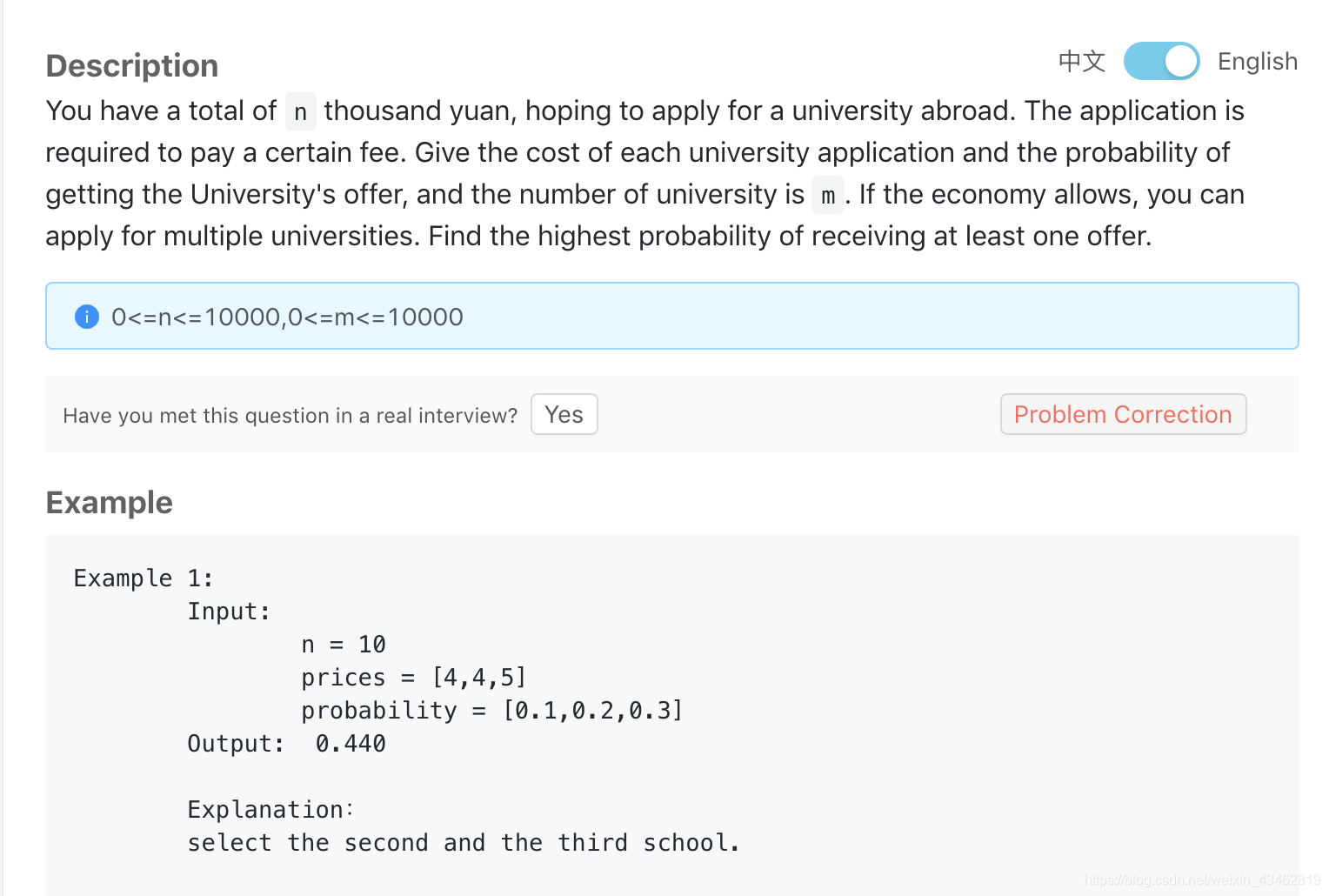
class Solution {
public:
/**
* @param n: Your money
* @param prices: Cost of each university application
* @param probability: Probability of getting the University's offer
* @return: the highest probability
*/
double backpackIX(int n, vector<int> &prices, vector<double> &probability) {
// write your code here
int sz = prices.size();
vector<vector<double>> dp(sz+1, vector<double>(n+1, 0.0));
for (int i = 1; i <= sz; ++i)
for (int j = 1; j <= n; ++j) {
if (prices[i-1] > j)
dp[i][j] = dp[i-1][j];
else
dp[i][j] = max(dp[i-1][j], 1.0-(1.0-dp[i-1][j-prices[i-1]])*(1.0-probability[i-1]));
}
return dp.back().back();
}
};
虽然超出内存限制,但是优化一下就可以了
LeetCode上的背包问题看下一篇博文。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号