机器学习各算法

一、线性回归

假设函数:

$Y = \theta^{T}X + B$

损失函数:

$Loss = \frac{1}{2m}[(\theta^{T}X + B) - Y_{real}]^{2}$

每个预测值和真实值之间的均方误差，Loss越小则表示模型越好

这个损失函数是一个凸函数，所以有全局最优解，即函数对$\theta$的偏导数等于0。求解时候对X特征加一列全是1，然后把B放到$\theta$向量中去

公式就可以改造为:$Loss = \frac{1}{2m}[(\theta^{T}X) - Y_{real}]^{2}$

数值解:

$\mathbf{\theta} = (\mathbf{X^{T}X})^{-1}\mathbf{X^{T}Y} $

这个求解过程可以参考https://www.cnblogs.com/pinard/p/5976811.html

梯度下降法求解:

损失函数对$\theta$的偏导为:

$\frac{\partial}{\partial\mathbf\theta}J(\mathbf\theta) = \mathbf{X}^T(\mathbf{X\theta} - \mathbf{Y})$

所以每次更新参数如下:

$\mathbf\theta= \mathbf\theta - \alpha\mathbf{X}^T(\mathbf{X\theta} - \mathbf{Y})$

 

二、逻辑回归

假设函数:

$g(z) = \frac{1}{1+e^{-z}}$

其中，$z =\theta^{T}X + B$

 

三、决策树

ID3算法只能处理离散值且无法做回归

实际上，CART算法的主体结构和ID3算法基本是相同的，只是在以下几点有所改变：

• 选择划分特征时，ID3使用信息熵量化数据集的混乱程度；CART使用基尼指数（Gini Index）和均方误差（MSE）量化数据集的混乱程度。
• 选定某切分特征时，ID3算法使用该特征所有可能的取值进行切分，例如一个特征有k个取值，数据集则被切成k份，创建k个子树；CART算法使用某一阈值进行二元切分，即在特征值的取值范围区间内选择一个阈值t，将数据集切分成两份，然后使用一个数据子集（大于t）构造左子树，使用另一个数据子集（小于等于t）构造右子树，因此CART算法创建的是二叉树。
• 对于已用于创建内部节点的特征，在后续运算中（创建子树中的节点时），ID3算法不会再次使用它创建其他内部节点；CART算法可能会再次使用它创建其他内部节点。所以很容易过拟合必须做限制。

 

四、KD树

 

 

 首先根据每个维度数据的方差，选择方差最大的那个维度，取其中位数作为节点分割，然后一层一层分割得到右边那二叉树模型。

然后就是得到测试点后进行搜索如下图

 

 

 查找（2，4.5）点的时候先按树形结构落到最后（4，7）的叶子节点，然后一步步向上回退

 

 

 

五、SVM

几何间隔，点到直线的距离：$\frac{|W^TX+b|}{\left \| W \right \|}$

因为分类正确所以有：$y_i(w_i^Tx_i+b)\geq 0$

然后直线方程可以等比例缩放的，所以可以令支撑向量上的点满足$|W^TX+b|=1$，那么对应正确分类约束条件就变成了$y_i(w_i^Tx_i+b)\geq 1$

此时优化目标就变成：$\frac{1}{\left \| W \right \|}$，使这个支撑向量上的点的margin要最大

 

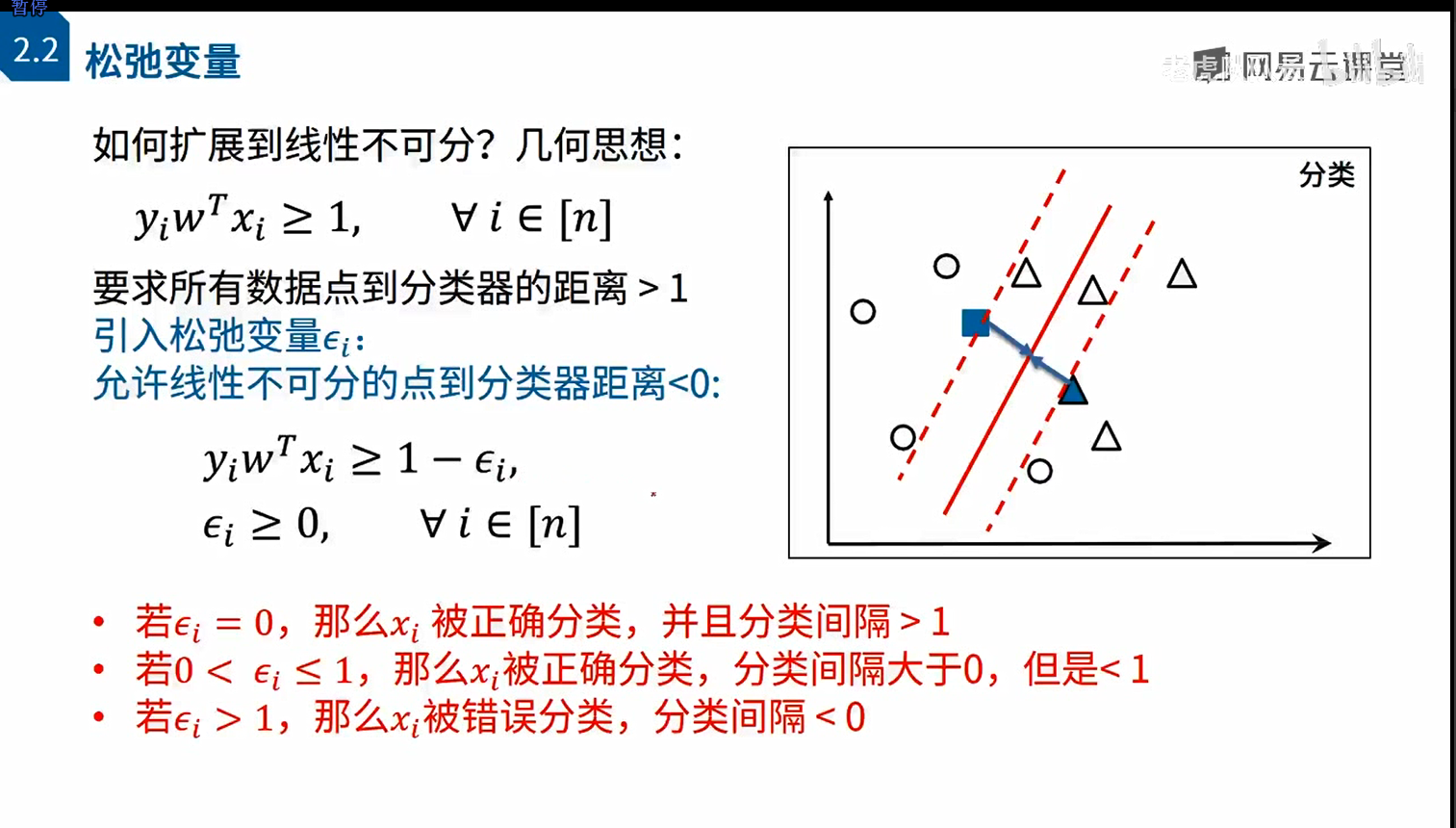
 对松弛变量的理解，第二种情况对应就是实体红线到右边虚线中的三角（分类正确但是不作为支持向量看待），第三种情况对应实体红线到左边虚线中的三角（分类错误）。每个数据点都有自己的松弛变量。

sklearn里svm的参数C就是最优化目标时松弛变量前面的C，C越大惩罚越大导致松弛变量就要越小，程序就要更朝着分类正确去前进（更容易拟合）