期权

一、期权影响因素

 

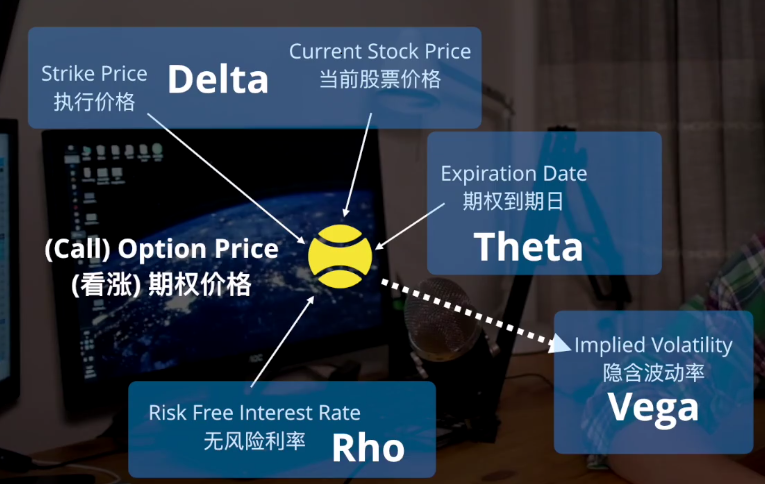
 Delta：期权价格对标的价格的一阶导

Gamma：Delta对标的价格的导数，也就是期权价格对标的价格的二阶导

Theta：期权价格对到期时间的一阶导

Vega：期权价格关于标的资产价格波动率的一阶导 

二、计算公式

历史波动率：

{

金字塔下表达式

1、计算以e为底的对数收益率：R_i = log(p_i / p_i-1)
2、计算对数收益率序列的标准差std
3、计算年波动率 = std * sqrt(250)

}

a:VOLATILITY(50,'SH510050');

a2:=ln(close)-ref(ln(close),1);
a3:=std(a2,49);
a4:a3*sqrt(250)

#传入一维数据，比如50日波动率，那么close就要求长度是50.
def GetVolatility(close):
    log_r =  np.log(close[1:]) - np.log(close[:-1])
    std_r = np.std(log_r,ddof=1)
    return std_r*np.sqrt(250)

 

BS公式

参考链接 https://nbviewer.jupyter.org/github/poppinkingone/jupyter_test/blob/master/Option.ipynb

 

from math import log,sqrt,exp
from scipy import stats
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd

class option():
    #参数分别表示
    #标的价，行权价，无风险利率，到期天数，波动率，期权最新价，call_put表示认购还是认沽
    def __init__(self,s,k,r,t,sigma,close,call_put='call'):
        self.s = s
        self.k = k
        self.r = r
        self.T = t/365
        self.sigma = sigma
        self.close = close
        self.call_put = call_put.lower()
        self.d1 = (log(self.s / self.k) + (self.r + 1 / 2 * self.sigma ** 2) * self.T) / (self.sigma * sqrt(self.T))
    #BS定价公式，返回期权理论价
    def call(self):
        '''
        st,k,r,T,sigma(T以年为单位，天数应该除以365)
        '''
        d1 = self.d1
        d2 = d1 - self.sigma * sqrt(self.T)
        call = self.s * stats.norm.cdf(d1, 0.0, 1.0) - self.k * exp(-self.r * self.T) * stats.norm.cdf(d2, 0.0, 1.0)
        return call
    def put(self):
        '''
        st,k,r,T,sigma(T以年为单位，天数应该除以365)
        '''
        d1 = self.d1
        d2 = d1 - self.sigma * sqrt(self.T)
        put = self.k * exp(-self.r * self.T) * stats.norm.cdf(-1 * d2) - 1 * self.s * stats.norm.cdf(-1 * d1)
        return put
    #获得delta
    def delta(self):
        '''
        n默认为1看涨期权的delta
        n为-1为看跌期权的delta
        '''
        if self.call_put == 'call':
            n = 1
        else:
            n = -1
        d1 = self.d1
        delta = n * stats.norm.cdf(n * d1)
        return delta

    # 获得gamma
    def gamma(self):
        d1 = self.d1
        gamma = stats.norm.pdf(d1) / (self.s * self.sigma * sqrt(self.T))
        return gamma

    # 获得theta
    def theta(self):
        '''
        n默认为1看涨期权的delta
        n为-1为看跌期权的delta
        '''
        if self.call_put == 'call':
            n = 1
        else:
            n = -1
        d1 = self.d1
        d2 = d1 - self.sigma * sqrt(self.T)
        theta = -1 * (self.s * stats.norm.pdf(d1) * self.sigma) / (2 * sqrt(self.T)) - n * self.r * self.k * exp(-self.r * self.T) * stats.norm.cdf(n * d2)
        return theta

    # 获得veag
    def vega(self):
        d1 = self.d1
        vega = self.s * sqrt(self.T) * stats.norm.pdf(d1)
        return vega
    #牛顿法迭代求隐含波动率
    def imp_vol_newton(self, sigma_est=1, it=100):
        if self.call_put == 'call':
            for i in range(it):
                d1 = (log(self.s / self.k) + (self.r + 1 / 2 * sigma_est ** 2) * self.T) / (sigma_est * sqrt(self.T))
                d2 = d1 - sigma_est * sqrt(self.T)
                call = self.s * stats.norm.cdf(d1, 0.0, 1.0) - self.k * exp(-self.r * self.T) * stats.norm.cdf(d2, 0.0,1.0)
                vega = self.s * sqrt(self.T) * stats.norm.pdf(d1)
                sigma_est -= (call - self.close) /vega
            return sigma_est
        else:
            for i in range(it):
                d1 = (log(self.s / self.k) + (self.r + 1 / 2 * sigma_est ** 2) * self.T) / (sigma_est * sqrt(self.T))
                d2 = d1 - sigma_est * sqrt(self.T)
                put = self.k * exp(-self.r * self.T) * stats.norm.cdf(-1 * d2) - 1 * self.s * stats.norm.cdf(-1 * d1)
                vega = self.s * sqrt(self.T) * stats.norm.pdf(d1)
                sigma_est -= (put - self.close) /vega
            return sigma_est

    # 二分法求隐含波动率
    def imp_vol_dichotomy(self):
        c_est = 0
        top = 3  # 波动率上限
        floor = 0  # 波动率下限
        sigma = (floor + top) / 2  # 波动率初始值
        if self.call_put == 'call':
            while abs(self.close - c_est) > 1e-8:
                d1 = (log(self.s / self.k) + (self.r + 1 / 2 * sigma ** 2) * self.T) / (sigma * sqrt(self.T))
                d2 = d1 - sigma * sqrt(self.T)
                call = self.s * stats.norm.cdf(d1, 0.0, 1.0) - self.k * exp(-self.r * self.T) * stats.norm.cdf(d2, 0.0,1.0)
                c_est = call
                # 根据价格判断波动率是被低估还是高估，并对波动率做修正
                if self.close - c_est > 0:  # f(x)>0
                    floor = sigma
                    sigma = (sigma + top) / 2
                else:
                    top = sigma
                    sigma = (sigma + floor) / 2
            return sigma
        else:
            while abs(self.close - c_est) > 1e-8:
                d1 = (log(self.s / self.k) + (self.r + 1 / 2 * sigma ** 2) * self.T) / (sigma * sqrt(self.T))
                d2 = d1 - sigma * sqrt(self.T)
                put = self.k * exp(-self.r * self.T) * stats.norm.cdf(-1 * d2) - 1 * self.s * stats.norm.cdf(-1 * d1)
                c_est = put
                # 根据价格判断波动率是被低估还是高估，并对波动率做修正
                if self.close - c_est > 0:  # f(x)>0
                    floor = sigma
                    sigma = (sigma + top) / 2
                else:
                    top = sigma
                    sigma = (sigma + floor) / 2
            return sigma

 

parameter = {}
parameter['标的价格'] = 2.858
parameter['行权价'] = 2.9
parameter['无风险利率'] = 0.044
parameter['到期天数'] = 15
parameter['历史波动率'] = 0.24269
parameter['期权最新价'] = 0.0167
parameter['call_put'] = 'call'


p1 = option(parameter['标的价格'],parameter['行权价'],parameter['无风险利率'],parameter['到期天数'],parameter['历史波动率'],parameter['期权最新价'],parameter['call_put'])

#希腊字母
p1.delta(),p1.gamma(),p1.theta(),p1.vega()

#隐波
p1.imp_vol_newton(),p1.imp_vol_dichotomy()

 

 三、波动率微笑

选取某一个月份的期权合约，把同一个行权价的call和put的隐波平均下得到一排隐波值

标准微笑图平直时候的隐波最小，两边成对称

实际中指数类期权往往呈现左高右低的倾斜，有一种解释是大部分人的现货都是持多头仓位，此时担心行情下跌所有会大量的买入虚值看跌期权来对冲风险。所以导致左半边隐波上升