机器学习的数学概念

 

似然函数

1、概率描述了已知参数时的随机变量的输出结果；似然则用来描述已知随机变量输出结果时，未知参数的可能取值。

涉及到似然函数的许多应用中，更方便的是使用似然函数的自然对数形式，即“对数似然函数”

2、最大似然估计是似然函数最初也是最自然的应用。上文已经提到，似然函数取得最大值表示相应的参数能够使得统计模型最为合理。从这样一个想法出发，最

大似然估计的做法是：首先选取似然函数，整理之后求最大值。实际应用中一般会取似然函数的对数作为求最大值的函数，这样求出的最大值和直接求最大值得

到的结果是相同的。

https://www.jianshu.com/p/af06571326ff

这个链接里的例子非常好，就是知道最后输出结果情况正正反反反，然后求解单次抛投硬币正面的概率为多少时，出现这个结果的可能性最大。

如果我们是求概率的话，就是知道一个硬币正面的概率比如是0.5，那么正正反反反的可能性是0.03125。如果单词概率是0.4那么正正反反反的可能性是0.03456

 

求解最大似然在线性回归那边会用到，参见https://www.cnblogs.com/yukizzc/p/11685038.html

贝叶斯

条件概率：

$P(A|B)=\frac{P(AB)}{P(B)}$

B发生的情况下A发生的概率  =  AB同时发生的概率 / B发生的概率

 

全概率公式：

$P(A)=\sum\limits_{i=1}^{n}P(B_{i})P(A|B_{i}) $

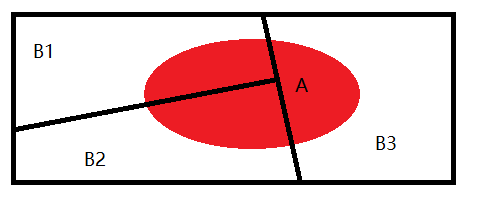看这个图理解，整个A事件可以分成和三个B事件相交集合的累加，相交部分用条件概率求得。

 

贝叶斯公式：

$P(B_{i}|A)=\frac{P(B_{i})P(A|B_{i})}{\sum\limits_{i=1}^{n}P(B_{i})P(A|B_{i}) }$

 

推导过程：

在事件B发生的条件下事件A发生的概率是　　　　$P(A|B)=\frac{P(AB)}{P(B)}$

在事件A发生的条件下事件B发生的概率是　　　　$P(B|A)=\frac{P(AB)}{P(A)}$

整理与合并上述两个方程式，便可以得到           $P(A|B)P(B) = P(AB) = P(B|A)P(A)$

 

范数

在