在通信中掌握一些数学知识是必要的,本篇博客记录一下部分概率论的知识以及常用的随机变量,这些内容出自与《数字通信》与《随机信号分析》
随机变量的函数
一个或多个随机变量的函数为:
$ Y=g(X) $ 或 $ Z=g(X_1,X_2,...,X_n) $
Y和Z是新的随机变量,自变量的多样性与不确定性导致因变量的多样性与不确定性,自变量的概率特性决定因变量的概率特性
一元函数
一元函数形如:$ Y=g(X) $
\[F_Y(y)=P[g(X)\leq y]=P[X\in \{x:g(x)\leq y\}]=\int_{\{x:g(x)\leq y\}}f_X(x)dx
\]
对于连续型随机变量,如果g(x)是单调递减或单调递增函数,则有下面的定理:
- 设Y=g(X),随机变量X具有概率密度$ f_X(x) $,-∞<x<∞,若g(x)处处可导且恒有g'(x)>0或g'(x)<0,则Y是连续型随机变量,其概率密度为:
\[ f_Y(y)=
\begin{cases}
f_X[h(y)]|h'(y)|,&a<x<b\\
0,&其他
\end{cases}
\]
其中a=min{g(-∞),g(∞)},b=max{g(-∞),g(∞)},h(y)是g(x)的反函数
其证明如下图所示:

二元函数
二元函数表示为:$ Z=g(X,Y) $
\[F_Z(z)= P[g(X,Y)\leq Z]=P[(X,Y)\in\{(x,y):g(x,y)\leq z\}]=\int_{(x,y):g(x,y)\leq z}f_{XY}(x,y)dxdy
\]
更一般的函数关系是如下的二元至二元的映射组:
\[\begin{cases}
U=g_1(X,Y)\\
V=g_2(X,Y)
\end{cases}
\]
若U和V有连续偏导数且存在唯一的反函数:
\[\begin{cases}
X=h_1(U,V)\\
Y=h_2(U,V)
\end{cases}
\]
可用下面的公式确定其联合密度函数:
\[f_{UV}(u,v)=f_{XY}[h_1(u,v),h_2(u,v)]|J|
\]
其中J为雅可比行列式:
\[ J=
\begin{vmatrix}
{\frac{\partial h_1}{\partial u}} & {\frac{\partial h_1}{\partial v}}\\
{\frac{\partial h_2}{\partial u}} & {\frac{\partial h_2}{\partial v}}
\end{vmatrix}=
(\begin{vmatrix}
{\frac{\partial g_1}{\partial x}} & {\frac{\partial g_1}{\partial y}}\\
{\frac{\partial g_2}{\partial x}} & {\frac{\partial g_2}{\partial y}}
\end{vmatrix})^{-1}
\]
瑞利和莱斯分布
理论分析与工程应用中常遇到正态随机变量的变换,这些变换衍生出一些重要的分布,其中瑞利与莱斯分布时无线电技术与通信工程等领域的常见分布,之所以放在这一节是因为其在通信领域的应用时的推导与随机变量的函数相关,至于分布的具体概率密度函数等参见后面的常用的随机变量一节
令复随机变量$ Z=X+jY=Re^{j\Theta} $,其中实部与虚部是同分布的零均值正态随机变量: $ X\sim N(0,\sigma^2) $ , $ Y\sim N(0,\sigma^2) $,且X与Y独立,讨论R与Θ的概率特性
R、Θ与X、Y之间的函数、反函数形式与雅可比行列式如下:
\[\begin{cases}
R=\sqrt{X^2+Y^2}\\
\Theta=arctan(Y/X)
\end{cases}
\]
\[\begin{cases}
x=rcos\theta\\
y=rsin\theta
\end{cases}
\]
\[ J=
\begin{vmatrix}
cos\theta & -rsin\theta\\
sin\theta & rcos\theta
\end{vmatrix}=r
\]
根据X与Y独立有:
\[f_{XY}(x,y)=f_X(x)f_Y(y)=\frac{1}{2\pi \sigma^2}e^{-\frac{(x^2+y^2)}{2\sigma^2}}
\]
于是
\[ f_{R\Theta}(r,\theta)=
\begin{cases}
f_{XY}(rcos\theta,rsin\theta)r, &r\geq 0\\
0, &r<0
\end{cases}=
\begin{cases}
\frac{r}{2\pi \sigma^2}e^{-\frac{r^2}{2\sigma^2}}, &r\geq 0\\
0, &r<0
\end{cases}
\]
由边缘概率密度得:
\[ f_R(r)=\int_0^{2\pi}f_{R\Theta}(r,\theta)d\theta=
\begin{cases}
\frac{r}{\sigma^2}e^{-\frac{r^2}{2\sigma^2}}, &r\geq 0\\
0, &r<0
\end{cases}
\]
\[ f_{\Theta}(\theta)=\int_0^{+\infty}f_{R\Theta}(r,\theta)dr=
\begin{cases}
\frac{1}{2\pi}, &\theta\in[0,2\pi)\\
0, &其他
\end{cases}
\]
其中R的分布被称为瑞利(Rayleigh)分布,故复变量Z的幅度为瑞利分布,相位为均匀分布,且$ f_{R\Theta}(r,\theta)=f_R(r)f_{\Theta}(\theta) $
,说明R与Θ相互独立
进一步地,如果X与Y的均值不为零,而是分别为$ \mu_X $ 与 $ \mu_Y $
随机变量的数字特征
随机变量的特征需要用一些数字特征来表达
数学期望
若随机变量X的密度函数为f(x),且$ \int_{-\infty}^{\infty}|x|f(x)dx<+\infty $,则:
\[E(X)=\int_{-\infty}^{\infty}xf(x)dx
\]
定义中的条件$ \int_{-\infty}^{\infty}|x|f(x)dx<+\infty $是为了保证E(X)存在,上式可能涉及冲激函数δ(x),特别当X为离散型时,f(x)完全由冲激函数组成,此时:
\[E(X)=\sum_ix_iP_i
\]
数学期望的基本性质有:
- 线性:$ E(aX+bY+c)=aE(X)+bE(Y)+c $,其中a、b、c为任意常数
- 若X1、X2等独立,则$ E(X_1...X_n)=E(X_1)E(X_2)...E(X_n) $
矩与联合矩
基于数学期望可以定义单个或多个随机变量的一批数字特征,统称为k阶矩(Moment)与k+r阶联合矩(Joint Moment)
- 绝对原点矩:$ E(|X|^k) $, $ E(|X|^k |Y|^r) $
- 原点矩:$ m_k=E(X^k) $, $ m_{k+r}=E(X^k Y^r) $
- 中心矩:$ \mu_k=E(X-EX)^k $, $ \mu_{k+r}=E[(X-EX)^k (Y-EY)^r] $
矩和联合矩中,特别重要的有:
(1)均方值:$ m_2=EX^2 $
(2)方差:$ \mu_2=E(X-EX)^2 $
其中方差(Variance)常记为σ2、Var(X)或D(X),并称σ为标准差,刻画X围绕EX的散布程度,方差的基本性质如下:
- $ Var(X)=EX^2-(EX) ^2 $
- $ Var(aX+c)=a^2Var(X) $,a、c为任意常数
- 如果Xi,i=1,...,n,两两独立,则$ Var(X_1+X_2+...+X_n)=Var(X_1)+Var(X_2)+...+Var(X_n) $
(3)联合矩:$ m_{11}=E(XY) $
(4)协方差:$ \mu_{11}=E[(X-EX)(Y-EY)] $
协方差(Covariance)常记为Cov(X,Y),其基本性质有:
- $ Cov(X,Y)=E(XY)-(EX)(EY) $
- $ Cov(X+Y,Z)=Cov(X,Z)+Cov(Y,Z) $
(5)相关系数
\[\rho_{XY}=\frac{Cov(X,Y)}{\sigma_X\sigma_Y}
\]
相关系数是归一化随机变量的协方差,有|ρXY|≤1,并且称:
\[ \rho=
\begin{cases}
0, &X与Y无关\\
\pm1, &X与Y线性(正或负)相关
\end{cases}
\]
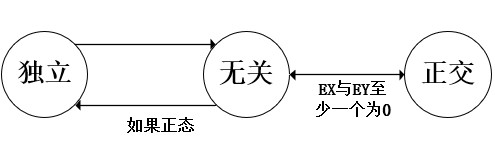
无关与正交
E(XY)、Cov(X,Y)与ρXY常用于刻画随机变量之间的关联程度,尤其是ρXY提供了一种归一化的测度
- 随机变量X与Y无关(Uncorrelated):Cov(X,Y)=0或ρXY=0,即E(XY)=(EX)(EY)
- 随机变量X与Y正交(Orthogonal):E(XY)=0
如果EX和EY中至少有一个为0时,则正交与无关等价
正交与无关是基于二阶矩的概念,而独立性是基于概率特性的概念,两者的出发角度不一样,一般而言独立比无关更为苛刻,但对于正态随机变量,两者是等同的。独立、无关与正交三者的关系如图所示:
常用的随机变量
伯努利随机变量
伯努利是取值为1和0,概率分别为p和1-p的离散二进制随机变量,因此该随机变量的概率质量函数(PMF)为:
\[P[X=1]=p,P[X=0]=1-p
\]
该随机变量的均值和方差为:
\[E[X]=p,VAR[X]=p(1-p)
\]
二项式随机变量
二项式随机变量是对n个具有共同参数p的独立伯努利随机变量的总和建模,该随机变量的PMF为:
\[P[X=k]=C_n^kp^k(1-p)^{n-k}
\]
随机变量的均值和方差为:
\[E[X]=np,VAR[X]=np(1-p)
\]
该随机变量可对n个比特在通信信道上传输而每个比特的错误概率为p时的错误数进行建模
均匀分布
均匀分布随机变量是连续随机变量,其PDF为:
\[ p(x)=
\begin{cases}
\frac{1}{b-a},&a\leq x\leq b\\
0,&其他
\end{cases}
\]
式中b>a,区间[a,b]是随机变量的取值范围,其均值和方差为:
\[E[X]=\frac{b-a}{2},VAR[X]=\frac{(b-a)^2}{12}
\]
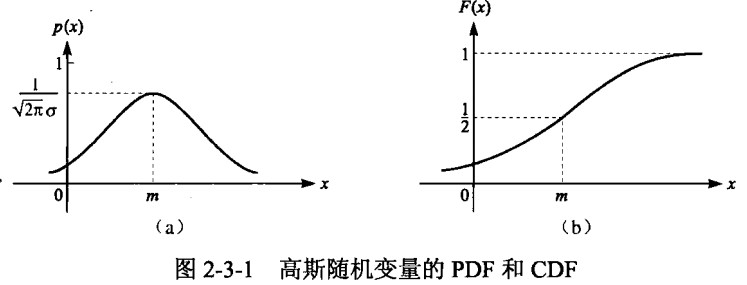
高斯(正态)随机变量
高斯随机变量由PDF及其两个参数m∈R和σ>0描述:
\[p(x)\frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(x-m)^2}{2\sigma^2}}
\]
通常用简洁形式$ N(m,\sigma^2) $表示高斯随机变量的PDF,该随机变量的均值和方差为:
\[E[X]=m,VAR[X]=\sigma^2
\]
m=0且σ=1的高斯随机变量称为标准随机变量
与高斯随机变量密切相关的一个函数是Q函数,这个函数在通信中常用,非常重要,定义如下:
\[Q(x)=P[N(0,1)>x]=\frac{1}{\sqrt{2\pi}}\int_x^{\infty}e^{-\frac{t^2}{2}}dt
\]
Q函数的一些重要性质如下:
\[Q(0)=\frac{1}{2}
\]
\[Q(\infty)=0
\]
\[Q(-\infty)=1
\]
\[Q(-x)=1-Q(x)
\]
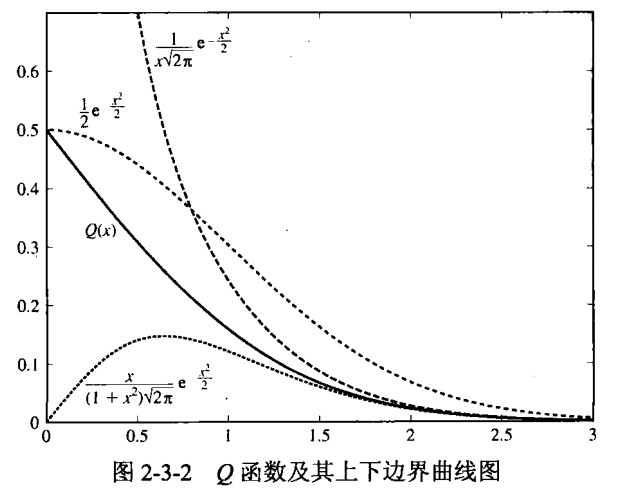
当x>0时,Q函数的一些有用边界为:
\[Q(x)\leq\frac{1}{2}e^{-\frac{x^2}{2}}
\]
\[Q(x)<\frac{1}{x\sqrt{2\pi}}e^{-\frac{x^2}{2}}
\]
\[Q(x)>\frac{x}{(1+x^2)\sqrt{2\pi}}e^{-\frac{x^2}{2}}
\]
Q函数边界的曲线如下图所示:
而高斯变量的CDF也可以用Q函数表示:
\[ F(x)=\int_{-\infty}^x\frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(t-m)^2}{2\sigma^2}}dt=1-\int_{x}^{\infty}\frac{1}{\sqrt{2\pi\sigma^2}}e^{-\frac{(t-m)^2}{2\sigma^2}}dt\\
=1-\int_{\frac{x-m}{\sigma}}^{\infty}\frac{1}{\sqrt{2\pi}}e^{-\frac{u^2}{2}}du=1-Q(\frac{x-m}{\sigma})
\]
式中引入了$ u=\frac{(t-m)}{\sigma} $的变化,高斯随机变量的PDF和CDF如下图所示:
另一个与Q函数密切相关的函数互补误差函数,定义如下:
\[erfc(x)=\frac{2}{\sqrt{\pi}}\int_x^{\infty}e^{-t^2}dt
\]
互补误差函数与Q函数的关系为:
\[Q(x)=\frac{1}{2}erfc(\frac{x}{\sqrt{2}})
\]
\[erfc(x)=2Q(\sqrt{2}x)
\]
高斯变量的特征函数为:
\[\phi_X(\omega)=e^{j\omega m-\frac{1}{2}\omega^2\sigma^2}
\]
需要注意的是,对于任何随机变量X,特征函数定义为$ \phi_X(\omega)=E[e^{j\omega X}] $
至于高斯随机变量的矩,可证明对于一个$ N(m,\sigma^2) $随机变量,有:
\[ E[(X-m)^n]=
\begin{cases}
1*3*5*...*(2k-1)\sigma^{2k}=\frac{(2k)!\sigma^{2k}}{2^kk!},&n=2k\\
0,&n=2k+1
\end{cases}
\]
N个独立的高斯随机变量的总和是一个高斯随机变量,其均值与方差分别为所有随机变量均值的总和与方差的总和
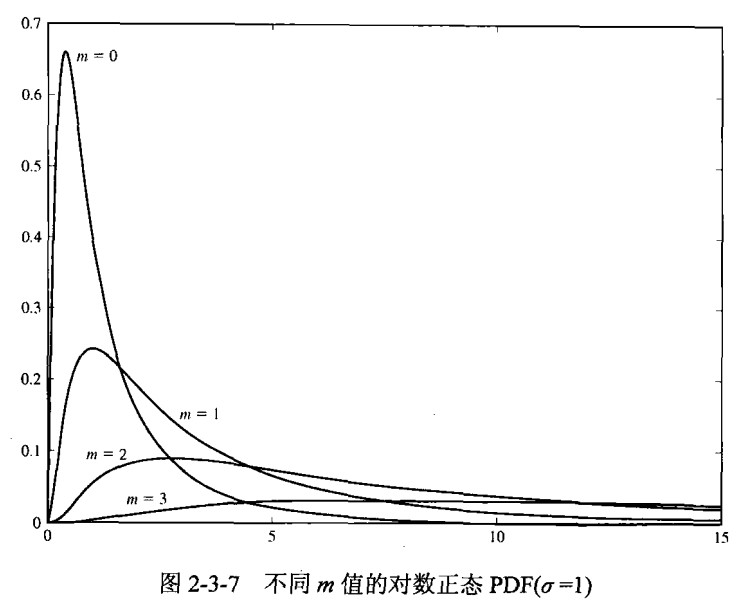
对数正态随机变量
假设随机变量Y服从正态分布,其均值为m且方差为$ \sigma^2 $,则通过变换:
\[Y=lnX
\]
可以定义一个与Y有关的新随机变量X,则X的PDF为:
\[ p(x)=
\begin{cases}
\frac{1}{\sqrt{2\pi\sigma^2}x}e^{-\frac{(lnx-m)^2}{2\sigma^2}},&x\geq0\\
0,&其他
\end{cases}
\]
对数正态的PDF如下图所示:
随机变量的均值和方差为:
\[E[X]=e^{m+\frac{\sigma^2}{2}},VAR[X]=e^{2m+\sigma^2}(e^{\sigma^2}-1)
\]
对数正态分布适合对移动无线通信中信号阴影效应建模,阴影效应是由大量障碍物(如高层建筑)引起
联合高斯随机变量
瑞利(Rayleigh)随机变量
如果X1和X2是两个iid高斯随机变量,每个变量服从$ N(0,\sigma^2) $,则
\[X=\sqrt{X_1^2+X_2^2}
\]
是瑞利随机变量,其PDF为:
\[ p(x)=
\begin{cases}
\frac{x}{\sigma^2}e^{-\frac{x^2}{2\sigma^2}},&x>0\\
0,&其他
\end{cases}
\]
下图是瑞利随机变量PDF的曲线:
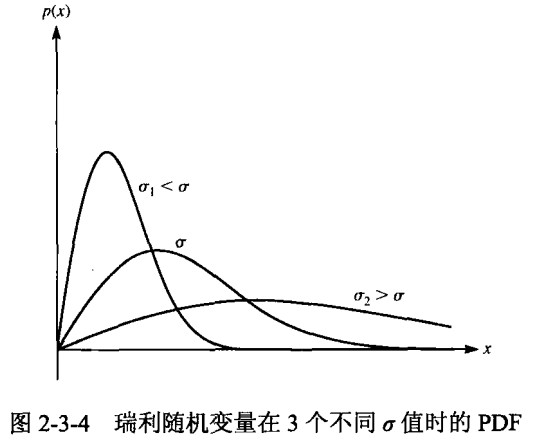
其均值和方差为:
\[E[X]=\sigma\sqrt{\frac{\pi}{2}},VAR[X]=(2-\frac{\pi}{2})\sigma^2
\]
对PDF积分可求得瑞利随机变量的CDF:
\[ F(x)=
\begin{cases}
1-e^{-\frac{x^2}{2\sigma^2}},&x>0\\
0,&其他
\end{cases}
\]
当有n个iid零均值高斯随机变量,其中每个Xi服从$ N(0,\sigma^2) $分布时,可以得到广义瑞利变量:
\[X=\sqrt{}
\]
一般的,瑞利随机变量的n阶矩为:
\[E[X^k]=(2\sigma^2)^{\frac{k}{2}}
\]
莱斯(Rice)随机变量
如果X1和X2是两个独立的高斯随机变量,分别服从 $ N(m_1,\sigma^2) $ 和 $ N(m_2,\sigma^2) $ 分布(即方差相同而均值可以不同),则:
\[X=\sqrt{X_1^2+X_2^2}
\]
是莱斯随机变量,其PDF为:
\[ p(x)=
\begin{cases}
\frac{x}{\sigma^2}e^{-\frac{x^2}{2\sigma^2}},&x>0\\
0,&其他
\end{cases}
\]








 浙公网安备 33010602011771号
浙公网安备 33010602011771号