二叉树遍历

相关阅读：b站左神

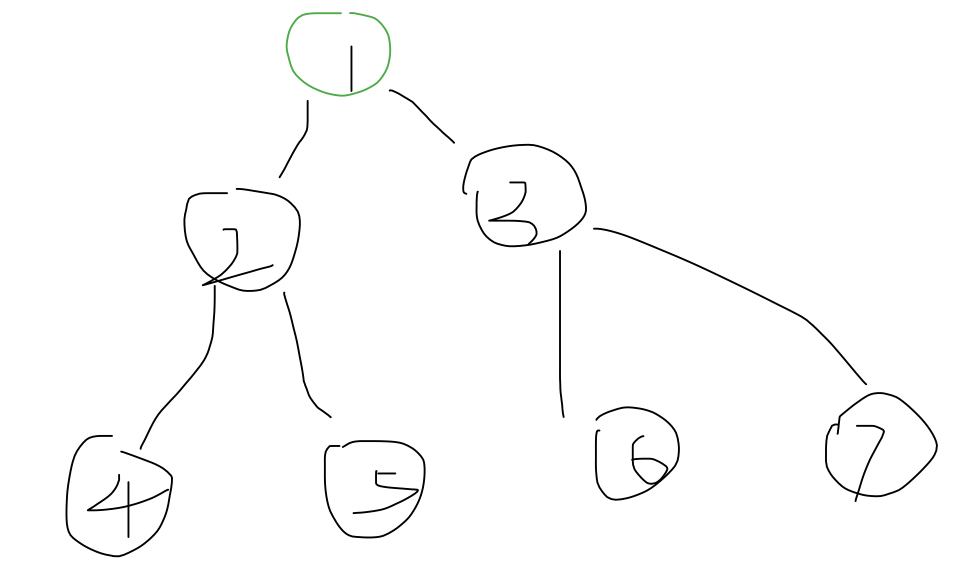
 对于如图所示的二叉树进行遍历使用递归，

第一次：1 -> 2 -> 4 -> 4 -> 4

从左子节点开始遍历，一直到4，4的左节点是空，返回4，开始右节点，依旧是空，所以还是返回4.

第二次：2-> 5 -> 5 -> 5

从4 返回到2开始遍历2的右节点 5，5的左右节点仍然是空，返回两次5.

第三次：1->3->6->6->6 

第四次：3->7->7->7->3->1 完成一轮遍历。

先序遍历：

class TreeNode():
    def __init__(self, val = 0, left = None, right = None) :
        self.val = val 
        self.left = left 
        self.right = right 

class Solution:
    def preorderTraversal(self, root) :
        if root == None:
            return [] 
        
        print(root.val)
        left = self.preorderTraversal(root.left) 
        right = self.preorderTraversal(root.right) 
        #print(root.val)
        #return [root.val] + left + right 

if __name__ == '__main__' :
    a = TreeNode(1)
    b = TreeNode(2)
    c = TreeNode(3)
    d = TreeNode(4)
    e = TreeNode(5)
    f = TreeNode(6)
    g = TreeNode(7)
    s = Solution() 
    a.left = b
    a.right = c 
    b.left = d 
    b.right = e 
    c.left = f 
    c.right = g
    s.preorderTraversal(a)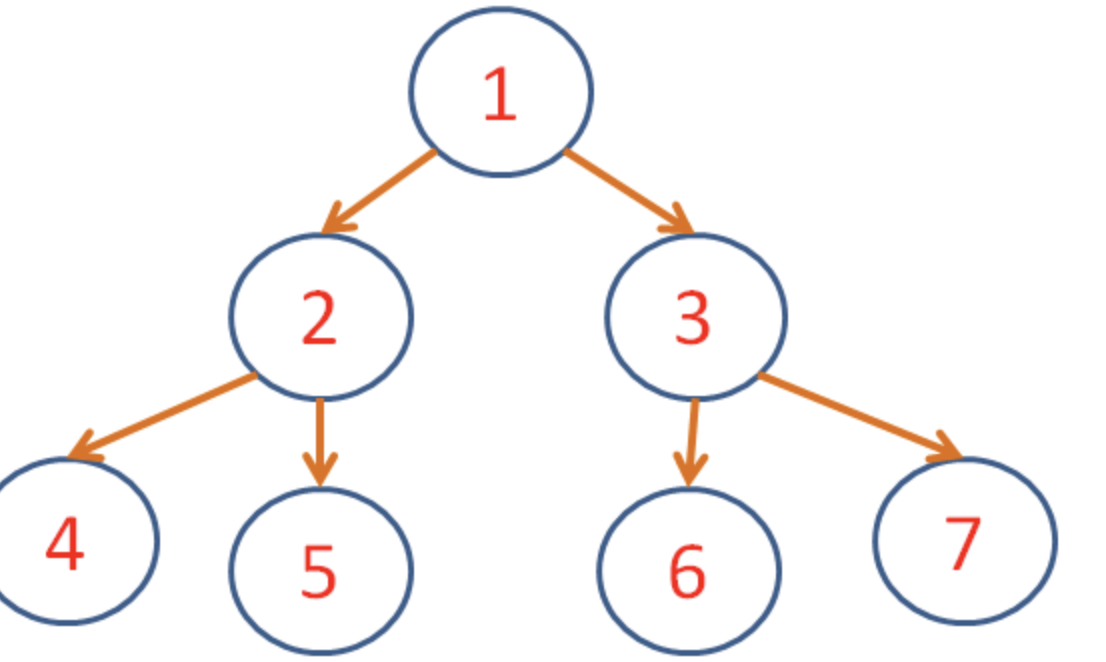 

当前对于二叉树的先序遍历，有如下解释：

在每一次的递归调用中，`left = self.preorderTraversal(root.left)` 和 `right = self.preorderTraversal(root.right)` 都会被执行，但它们是顺序执行的，而不是并行执行。

以下是该递归调用的简要概述：

1. 当你首次调用 `preorderTraversal(a)` 时（对于根节点 a 或节点 1），
    - 首先，执行 `left = self.preorderTraversal(root.left)`，进入左子树，也就是 b（或节点 2）。
    
2. 在这个新的递归调用 `preorderTraversal(b)` 中，
    - 同样首先执行 `left = self.preorderTraversal(root.left)`，进入左子树，也就是 d（或节点 4）。
  
3. 在 `preorderTraversal(d)` 中，
    - 因为 d（或节点 4）的左右子树都是 `None`，所以这一层的 `left = self.preorderTraversal(root.left)` 和 `right = self.preorderTraversal(root.right)` 都会立即返回空列表。
  
4. 一旦 `preorderTraversal(d)` 执行完毕，控制权会返回到 `preorderTraversal(b)`，继续执行还未执行的 `right = self.preorderTraversal(root.right)`，这时进入右子树 e（或节点 5）。

5. 同理，当 `preorderTraversal(b)` 执行完毕，控制权会返回到最开始的 `preorderTraversal(a)`，然后执行还未执行的 `right = self.preorderTraversal(root.right)`，这时进入右子树 c（或节点 3）。

简而言之，`left = self.preorderTraversal(root.left)` 和 `right = self.preorderTraversal(root.right)` 都会在每一层的递归中被执行，但是由于是递归，我们需要先 "深入" 到最底层的节点，然后 "回溯" 执行未完成的右子树递归调用。这就是为什么看起来好像我们在返回到上一级之后才执行右子树的原因。这种深度优先的遍历顺序符合先序遍历（根-左-右）的规则。

#非递归方式，迭代遍历
def preOrderTravese(node) :
    if node != None:
        stack = [node] 
        while stack:
            node = stack.pop() 
            print(node.val) 
            if node.right:
                stack.append(node.right) 
            if node.left:
                stack.append(node.left)

1）每次弹出栈中的一个节点 cur

2）打印cur

3) 将cur.right先压入栈中，再将cur.left 压入栈中 （如果有） 

4）循环上述

以上图二叉树为例，先将1压入栈中，之后弹出并打印，将3，2 压入栈中。弹出2并打印，再将5，4压入，弹出4，5并打印，因为不存在左右子节点。

中序遍历：左头右

迭代法：每棵子树整棵树左边届进栈，依次弹出的过程中，对弹出节点的右树重复。

def inorderTraverse(node) :
    if node != None :
        stack = [] 
        while stack or node : 
            if node:
                #node 入栈，寻找所有左边界节点入栈
                #直到左边界节点的左子为空
                stack.append(node) 
                node = node.left 
            else:
                #此时弹出当前节点并打印
                node = stack.pop() 
                print(node.val) 
                #依次将右节点放入
                node = node.right 
                

后序遍历：左右头

迭代法：弹出当前节点，并将当前节点放入收集栈中。先左再右，循环。

def postOrderTravese(node) :
    res = []
    if node != None:
        stack1 = [] 
        stack2 = [] 
        stack1.append(node) 
        while stack1 :
            node = stack1.pop()
            stack2.append(node) 
            if node.left:
                stack1.append(node.left) 
            if node.right:
                stack1.append(node.right) 
        while stack2:
            res.append(stack2.pop().val) 

        return res