使用朴素贝叶斯对电影评论分类

@

目录

• 使用朴素贝叶斯对电影评论分类
  • 1.数据集讲解：
  • 2.具体实现：
  • 3.实验结果：
• 实验总结

使用朴素贝叶斯对电影评论分类

1.数据集讲解：

​ 该数据集是IMDB电影数据集的一个子集，已经划分好了测试集和训练集，训练集包括25000条电影评论，测试集也有25000条，该数据集已经经过预处理，将每条评论的具体单词序列转化为词库里的整数序列，其中每个整数代表该单词在词库里的位置。例如，整数104代表该单词是词库的第104个单词。为实验简单，词库仅仅保留了10000个最常出现的单词，低频词汇被舍弃。每条评论都具有一个标签，0表示为负面评论，1表示为正面评论。

​ 训练数据在train_data.txt文件下，每一行为一条评论，训练集标签在train_labels.txt文件下，每一行为一条评论的标签；测试数据在test_data.txt文件下，测试数据标签未给出。

2.具体实现：

1. 取出数据集：

   从txt中取出训练集与测试集：

   with open("test/test_data.txt", "rb") as fr:
   
     test_data_n = [inst.decode().strip().split(' ') for inst in fr.readlines()]
   
     test_data = [[int(element) for element in line] for line in test_data_n]
   
   test_data = np.array(test_data)
   

2. 数据处理：

   对每条评论，先将其解码为英文单词，再键值颠倒，将整数索引映射为单词。

   把整数序列编码为二进制序列。

   最后把训练集标签向量化。

   # 将某条评论解码为英文单词
   
   word_index = imdb.get_word_index() # word_index是一个将单词映射为整数索引的字典
   
   reverse_word_index = dict([(value, key) for (key, value) in word_index.items()])
   
   # 键值颠倒，将整数索引映射为单词
   
   decode_review = ' '.join(
   
     [reverse_word_index.get(i - 3, '?') for i in train_data[0]]
   
   ) 
   
   \# 将评论解码
   
   \# 注意，索引减去了3，因为0,1,2是为padding填充
   
   \# "start sequence"序列开始，"unknow"未知词分别保留的索引
   
    
   
   \# 将整数序列编码为二进制矩阵
   
   def vectorize_sequences(sequences, dimension=10000):
   
     results = np.zeros((len(sequences), dimension)) # 创建一个形状为(len(sequences), dimension)的矩阵
   
     for i, sequence in enumerate(sequences):
   
       results[i, sequence] = 1 # 将results[i]的指定索引设为 1
   
     return results
   
   x_train = vectorize_sequences(train_data)
   
   x_test = vectorize_sequences(test_data)
   
   \# 标签向量化
   
   y_train = np.asarray(train_labels).astype('float32')
   

3. 建立模型：

   可选多项式模型或者伯努利模型。

   二者的计算粒度不一样，多项式模型以单词为粒度，伯努利模型以文件为粒度，因此二者的先验概率和类条件概率的计算方法都不同。
   计算后验概率时，对于一个文档d，多项式模型中，只有在d中出现过的单词，才会参与后验概率计算，伯努利模型中，没有在d中出现，但是在全局单词表中出现的单词，也会参与计算，不过是作为“反方”参与的。
   当训练集文档较短，也就说不太会出现很多重复词的时候，多项式和伯努利模型公式的分子相等，多项式分母值大于伯努利分子值，因此多项式的似然估计值会小于伯努利的似然估计值。
   所以，当训练集文本较短时，我们更倾向于使用伯努利模型。而文本较长时，我们更倾向于多项式模型，因为，在一篇文档中的高频词，会使该词的似然概率值相对较大。

   使用拉普拉斯平滑

   alpha:先验平滑因子，默认等于1，当等于1时表示拉普拉斯平滑。

   # model = MultinomialNB()
   model = BernoulliNB()
   model.fit(X_train, y_train)
   

4. 输出测试集上的预测结果：

   将结果写入txt

   # model evaluation
   print("model accuracy is " + str(accuracy_score(y_test, y_pred)))
   print("model precision is " + str(precision_score(y_test, y_pred, average='macro')))
   print("model recall is " + str(recall_score(y_test, y_pred, average='macro')))
   print("model f1_score is " + str(f1_score(y_test, y_pred, average='macro')))
   
   des = y_pred_local.astype(int)
   np.savetxt('Text3_result.txt', des, fmt='%d', delimiter='\n')
   

3.实验结果：

使用多项式模型：

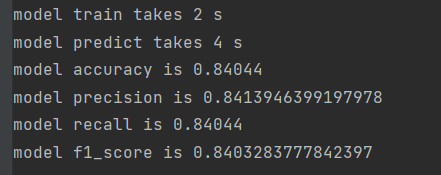
使用伯努利模型：

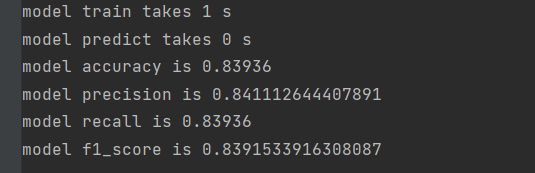
在该场景下，两者差别不大。

实验总结

1. 贝叶斯概率及贝叶斯 准则提供了一种利用已知值来估计位置概率的有效方法；
2. 朴素贝叶斯假设数据特征之间相互独立，虽然该假设在一般情况下并不严格成立，但使用朴素贝叶斯进行分类，仍然可以取得很好的效果；
3. 贝叶斯网络的优点：在数据较少的情况下仍然有效，可以处理多类别问题；
4. 贝叶斯网络的缺点：对输入数据的准备方式较为敏感。
5. 拉普拉斯平滑对于改善朴素贝叶斯分类器的分类效果有着积极的作用。