Test 1022
T1 AERODROM (二分答案
TimeLimit: 1000MS
Memory Limit: 32768KB
\(N\)个登机口,办理登机业务,第\(i\)个窗口的单位办理时间为\(T_i\),\(M\)个人办理登机业务,他们可以选择最佳的方案,不考虑换人和换窗口的时间,所有窗口是同时计时的,即同时开始办理业务,请输出所有人都登机的最少时间。
如样例\(1\):
2个窗口,6个人,第一个窗口的单位时间是7,第二个是10, 一二个人分别在两个窗口办理,7秒时第三个人可在第一个窗口开始办理,10秒时,第四人开始在窗口二办理,时间14时,第五人一窗口。在时间20,窗口2可以使用,如果第六人在此办理,总时间将是30秒,如果等1秒在一窗口办理,则总时间是28秒。
输入:
第一行两个正整数 \(N (1 ≤ N ≤ 100 000)\),
窗口数,和\(M (1 ≤ M ≤ 1 000 000 000)\), 登机人数。
以下每行一个数\(T_i\)表示第\(i\)个窗口的单位办理时间 \((1 ≤ Ti ≤ 10^9)\).
输出 :
一个数,最少办理时间。
input
2 6
7
10
output
28
input
7 10
3
8
3
6
9
2
4
output
8
时间就是每个窗口时间的最大值,求最大值的最小值,用二分答案;
\(Code\)
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=100005,M=1000000005;
int n,m;
int a[N],mins=0x7fffffff;
ll l,r;
inline int read()
{
int x=0,f=1;char st=getchar();
while(st<'0'||st>'9'){if(st=='-') f=-1;st=getchar();}
while(st>='0'&&st<='9') x=x*10+st-'0',st=getchar();
return x*f;
}
inline bool check(ll mid)
{
ll tmp=0;
for(int i=1;i<=n;i++)
{
tmp+=mid/a[i];
if(tmp>=m) return 1;
}
return 0;
}
int main()
{
freopen("aerodrom.in","r",stdin);
freopen("aerodrom.out","w",stdout);
n=read();m=read();
for(int i=1;i<=n;i++)
{
a[i]=read();
mins=min(mins,a[i]);
}
r=(ll)mins*m;
while(l<r)
{
ll mid=l+r>>1;
if(check(mid)) r=mid;
else l=mid+1;
}
printf("%lld",l);
fclose(stdin);
fclose(stdout);
return 0;
}
T2 HERKABE (trie
TimeLimit: 1000MS
Memory Limit: 32768KB
给出\(N\)个由大写字母构成的名字,现在要求对名字排序,要求有相同前缀的单词要排在一起,问共有多少种排法。
输入:
第一行一个正整数 \(N (3 ≤ N ≤ 3000)\), 名字的个数。
以下N行,每行一个名字长度界于\(1\)到 \(3000\) 名字无重复且按任意顺序给出。.
输出:
一行一个正整数表示方案总数。由于数据大要求输出模\(1000 000 007\)的值.
input
3
IVO
JASNA
JOSIPA
output
4
input
5
MARICA
MARTA
MATO
MARA
MARTINA
output
24
input
4
A
AA
AAA
AAAA
output
8
这道题目有故意卡内存之嫌;
先理解题目;
第一个样例对我们没有太大帮助;
第二个样例;
最长的公共前缀是MART,所以MARTA,MARTINA必须排在一起;有\(2!\)种
把这两个看成一个整体\(x\),接下来的最长公共前缀是MAR,所以\(x\),MARICA,MARA必须放在一起;有\(3!\)种;
再把这些看成一个整体\(y\),接下来的最长公共前缀是MA,所以\(y\),MATO必须放在一起;有\(2!\)种;
总共有\(2!*2!*3!=24\)种;
发现,这不就是一颗\(trie\)树吗;
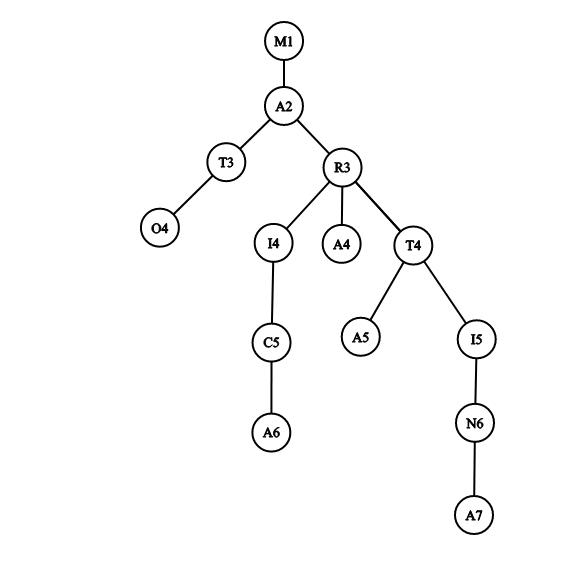
其实答案就是\(trie\)数中,每个节点的子节点个数的阶乘的乘积;
然后写棵\(trie\)就可以了
然后第三个样例过不了,当某个字符串是另一个字符串的前缀时,我们发现这一个字符串是没有结束符的,我们可以在每个字符串后面加一个\('Z'+1\),这样就不会有任何两个字符串互为前缀了;
然后就会\(MLE\);
时间复杂度是\(O(n^2)\)
优化
- 用vector 代替字符集;
- 排序后模拟\(trie\)树;
这种办法比较好想,想用\(O(n^2logn)\)按字典序排序,有相同前缀的一定在一起;
我们一位一位搜,找下一位有多少种不同的字符(就是\(trie\)树中这个节点的子节点个数),过程中统计子节点个数的阶乘,当只有一个子节点时返回;
与\(trie\)树时间复杂度一样,这部分是\(O(n^2)\);
\(Code\)
#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=3005,mod=1000000007;
int n;
struct skr
{
char s[N];
int len;
bool operator<(skr w)const
{
for(int i=0;i<max(len,w.len);i++)
if(s[i]<w.s[i]) return 1;
else if(s[i]>w.s[i]) return 0;
}
}a[N];
ll ans=1,nm[N];
inline int read()
{
int x=0,f=1;char st=getchar();
while(st<'0'||st>'9'){if(st=='-') f=-1;st=getchar();}
while(st>='0'&&st<='9') x=x*10+st-'0',st=getchar();
return x*f;
}
inline void dfs(int x,int l,int r) //搜第x位,搜索区间是l~r
{
if(l>=r) return ;
int num=0;
int L=l,R=l;
for(int i=l;i<=r;i++)
{
if(a[i].s[x]==a[L].s[x]) R=i;
else
{
num++;
dfs(x+1,L,R);
L=i;
}
}
num++;
if(L==r) R=r;
dfs(x+1,L,R);
ans=ans*nm[num]%mod;
}
int main()
{
freopen("herkabe.in","r",stdin);
freopen("herkabe.out","w",stdout);
n=read();
for(int i=1;i<=n;i++)
{
scanf("%s",a[i].s);
a[i].len=strlen(a[i].s);
a[i].s[a[i].len]='Z'+1;
a[i].len++;
}
nm[0]=1;
for(int i=1;i<=n;i++)
nm[i]=nm[i-1]*i%mod;
sort(a+1,a+1+n);
dfs(0,1,n);
printf("%lld",ans);
fclose(stdin);
fclose(stdout);
return 0;
}
- 压缩\(trie\)树
实际上是压缩尾缀,将没有分叉的节点(单链)合成一个节点,这样建成的\(trie\)树,除了叶子结点,每个节点有最少\(2\)个子节点,最多有字符集大小个子节点。节点个数是字符串个数等级的,可以大规模压缩空间;
比如这是一棵压缩了的\(trie\)树:

(图片来自网络
T2 HERKABE (扩展域并查集
TimeLimit: 1000MS
Memory Limit: 32768KB
给出一个数字\(N\)表示有\(N\)个\(32\)位无符号数\((0\sim 2^{32}-1)\),我们可以进行如下两个操作
操作\(1\)表示把第\(K\)个数后\(M\)位转到最前面;
操作\(2\)表示把第\(K\)个数和第\(L\)个数进行\(XOR\)运算。
我们最初不知道这\(N\)个数的值,但我们知道每一个\(2\)操作后的结果,请推出每一个数最初的值。如果有多种解,输出字典序最小的。(如果第\(K-1\)个数一样,则第\(K\)个数小的则小)
输入 :
第一行两个正整数: \(N (2 ≤ N ≤ 100 000)\), 变量的个数。和 \(E (1 ≤ E ≤ 100 000)\), 操作的个数。
接下来\(E\)行,按执行的顺序给出每一个操作和操作后的答案。 \((1 ≤ K, L ≤ N, 0 ≤ M < 32)\).
每次操作的答案大小\(0\) 到$ 2^{32}– 1$,二进制异或的值是按\(10\)进制给出的。
输出:
一行,\(N\)个值,表示变量最初的可能值。
如果找不到合适的方案,则输出\(-1\)。
input
3 3
2 1 2
1
2 1 3
2
2 2 3
3
output
0 1 2
input
4 6
2 4 2
3
2 4 1
6
1 3 1
2 3 1
2
1 2 2
2 2 3
7
output
5 0 14 3
input
5 6
2 4 2
10
2 5 3
2
2 2 3
1
2 1 4
3
1 3 1
2 3 4
2147483663
output
15 6 7 12 5
我们先把\(n\)个数拆成\(n\)个二进制串;
从第二种个操作入手,如果得到的结果第\(i\)位是\(1\),意味着第\(K\)个和第\(L\)个数的第\(i\)位是不一样的,否则是一样的;
那\(1\)操作呢,我们发现它只是把我们的二进制串移了个位置,可以记录一个\(r[i]\)表示第\(i\)个串被右移了多少位;
这样我们得到了很多约束条件,要求一种构造方法,使每个节点有一个合适的赋值(\(0/1\));
这就是\(2-SAT\)模型了,但这道题又会\(MLE\);
这类问题也可以用并查集扩展域来做,应为只有两种取值,我们视每个数的每一位为一个节点,每个节点有两个域,\(0\)域和\(1\)域;
如果两个点相同,则把他们的,\(0\)域相连,\(1\)域相连;
代表其中一个节点选\(0(或1)\),另一个必须选\(0(或1)\);
若不同,则\(1\)域与\(0\)域相连,\(0\)域与\(1\)域相连;
如果有一个节点的\(0\)域与\(1\)域相连了,则输出\(-1\);
确保了有合法构造方案之后,我们可以用贪心得到字典序最小的构造方案;
从第一个数的最高位开始;
优先选\(0\),如果其\(0\)域的根被取了与它所在域合适的值,当前节点就取\(0\);
\(1\)域同样;
如果两个域都没有合适的值,当前节点优先选\(0\),并应当把其\(0\)域根节点的取值赋成这个根节点所在域的值,相当于把这个集合的节点都赋了值;
\(Code\)
#include<bits/stdc++.h>
#define c n*32
#define ll long long
using namespace std;
const int N=100005;
int n,e,opt;
char ans[N][35];//卡内存
int r[N];
int fa[N*32*2],f1,f2;
ll sq[35],ra;
inline int read()
{
int x=0,f=1;char st=getchar();
while(st<'0'||st>'9'){if(st=='-') f=-1;st=getchar();}
while(st>='0'&&st<='9') x=x*10+st-'0',st=getchar();
return x*f;
}
inline int get(int x)
{
return fa[x]==x?x:fa[x]=get(fa[x]);
}
int main()
{
freopen("procesor.in","r",stdin);
freopen("procesor.out","w",stdout);
n=read();e=read();
memset(fa,-1,sizeof fa);
for(int i=0;i<=n*32*2;i++)
fa[i]=i;
for(int i=1;i<=e;i++)
{
opt=read();
if(opt==1)
{
int x=read(),y=read();
r[x]=(r[x]+y)%32;
}
else
{
int x=read(),y=read(),z;
scanf("%lld",&z);
for(int j=0;j<32;j++)
if((z>>j)&1)
{
int x1=(j+r[x])%32,x2=(j+r[y])%32;
f1=get((x-1)*32+x1),f2=get((y-1)*32+x2+c);
if(f1!=f2)
fa[f1]=f2;
f1=get((x-1)*32+x1+c),f2=get((y-1)*32+x2);
if(f1!=f2)
fa[f1]=f2;
}
else
{
int x1=(j+r[x])%32,x2=(j+r[y])%32;
f1=get((x-1)*32+x1),f2=get((y-1)*32+x2);
if(f1!=f2)
fa[f1]=f2;
f1=get((x-1)*32+x1+c),f2=get((y-1)*32+x2+c);
if(f1!=f2)
fa[f1]=f2;
}
}
}
for(int i=0;i<32*n;i++)
{
f1=get(i),f2=get(i+c);
if(f1==f2)
{
printf("-1");
fclose(stdin);
fclose(stdout);
return 0;
}
}
for(int j=1;j<=n;j++)
for(int i=0;i<32;i++)
ans[j][i]=2;//初始
for(int j=1;j<=n;j++)
for(int i=31;i>=0;i--)
{
bool fl1=0,fl2=0;
f1=get((j-1)*32+i);//0
f2=get((j-1)*32+i+c);//1
if(f1>=c) f1-=c,fl1=1;
if(f2>=c) f2-=c,fl2=1;
if(ans[(f1)/32+1][f1%32]==(fl1==1))
{
ans[j][i]=0;
}
else
{
if(ans[(f2)/32+1][f2%32]==(fl2==1))
ans[j][i]=1;
else
{
ans[j][i]=0;
ans[(f1)/32+1][f1%32]=fl1;
}
}
}
sq[0]=1;
for(int i=1;i<=32;i++)
sq[i]=sq[i-1]*2;
for(int j=1;j<=n;j++)
{
ra=0;
for(int i=0;i<32;i++)
{
ra=ra+sq[i]*ans[j][i];
}
printf("%lld ",ra);
}
fclose(stdin);
fclose(stdout);
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号