数据结构：关于各种二叉树（防记混）
二叉树：
（一些性质、公式）
- \(n=n_0+n_1+n_2\)
- \(n=n_1+2n_2+1\)（\(n=分支数+1\)、\(分支数=n_1+2n_2\)）
- \(n_0=n_2+1\)（由以上两式可得）
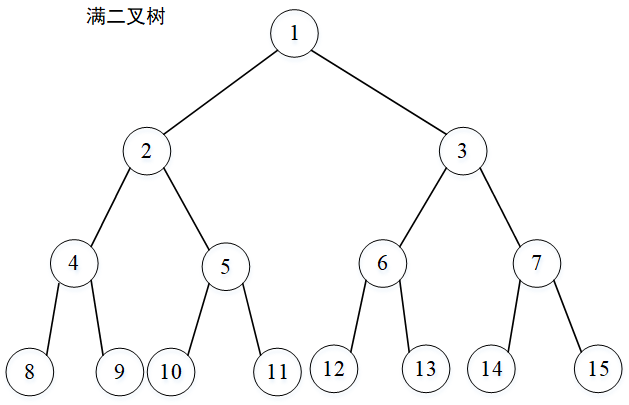
满二叉树：
深度为\(k\) ，且含有\(2^k-1\)个节点的二叉树
完全二叉树：
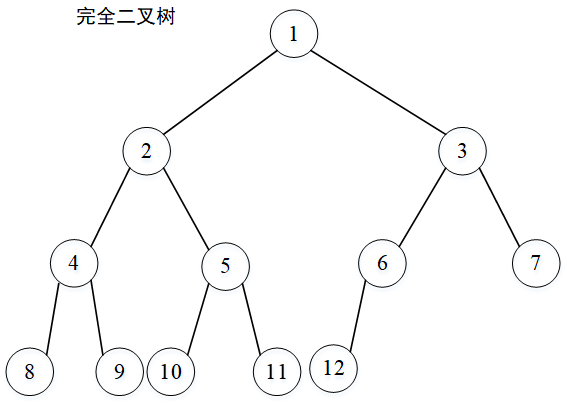
深度为k，n个节点，当且仅当其每个节点与深度为k的满二叉树一一对应时，其为完全二叉树。
a. 其特点：
- 叶子结点只可能在层次最大的两层上出现;
- 对任一个节点，其右子树下的子孙最大层次为\(l\) ，则其左子树下的子孙的最大层次必为\(l\) 或\(l+1\) 。
b. 具有n个节点的完全二叉树的深度：\(k=\lfloor log_2n \rfloor+1\)
二叉查找树/二叉排序树：
左子树(如果不为空)上的结点值小于根结点的值；右子树(如果不为空)上的结点值大于根结点的值。
平衡二叉树(AVL树) ：
一种特殊的二叉排序树，希望二叉排序树的高度尽可能小。
a. 平衡二叉树是具有如下特征的二叉排序树：
- 左右子树深度之差绝对值不超过1；
- 其左右子树也是平衡二叉树。
注意：平衡二叉树的平衡调整方法
