贪心算法与递归
贪心算法
分金条问题
会议室场次问题
花费资金做项目问题
取中位数问题
字典序最小问题
暴力递归
汉诺塔问题
打印字符串的全部子序列
打印字符串全排列(有重复)
打印字符串全排列(无重复)
数字转字符串
背包问题
纸牌问题
N皇后问题
分金条问题
一块金条切成两半,是需要花费和长度数值一样的铜板的。比如长度为20的金 条,不管切成长度多大的两半,都要花费20个铜板。
一群人想整分整块金条,怎么分最省铜板? 例如,给定数组{10,20,30},代表一共三个人,整块金条长度为10+20+30=60。 金条要分成10,20,30三个部分。 如果先把长度60的金条分成10和50,花费60; 再把长度50的金条分成20和30,花费50;一共花费110铜板。 但是如果先把长度60的金条分成30和30,花费60;再把长度30金条分成10和20, 花费30;一共花费90铜板。 输入一个数组,返回分割的最小代价
思路:
首先将数组的值进到优先级队列里去,有一个小到大的排序过程,然后依次取最大的两个值进行计算代价
然后将计算完成之后的结果再放入队列尾部,不断重复,一直到队列为空。
每次累加最后返回的值,就是分割的最小代价。
int lessMoney(int array[],int len) { priority_queue<int> pQ; for (int i = 0; i < len; i++) { pQ.push(array[i]); } int sum = 0; int cur = 0; int a = 0; while (pQ.size() > 1) { a = pQ.top(); pQ.pop(); cur = a + pQ.top(); pQ.pop(); sum += cur; pQ.push(cur); } return sum; }
会议室场次问题
一些项目要占用一个会议室宣讲,会议室不能同时容纳两个项目的宣讲。 给你每一个项目开始的时间和结束的时间(给你一个数组,里面是一个个具体的项目),你来安排宣讲的日程,要求会议室进行的宣讲的场次最多。 返回这个最多的宣讲场次。
思路:
首先定义项目类,开始时间和结束时间,按结束时间进行从小到大的排序
start是可以开始的时间,传参进来为0,从0点开始。
如果start的时间是在当前的项目的时间之前或者刚刚好,则可以开展的场次结果加1,并且将这次结束时间作为下次可开始的时间。
class Program { public: Program(int s,int e):start(s),end(e){} int start; int end; }; bool compare(Program a, Program b) { return a.end < b.end; } int bestArrange(Program program[], int start) { int len = sizeof(program) / sizeof(program[0]); sort(program, program + len, compare); int result = 0; for (int i = 0; i < len; i++) { if (start <= program[i].start) { result++; start = program[i].end; } } return result; }
花费资金做项目问题
输入:
正数数组costs
正数数组profits
正数k
正数m
含义:
costs[i] 表示i号项目的花费,profits[i] 表示i号项目在扣除花费之后还能挣到的钱(利润) ,k表示你只能串行的最多做k个项目 ,m表示你初始的资金
说明: 你每做完一个项目,马上获得的收益,可以支持你去做下一个项目。
输出: 你最后获得的最大钱数。
思路:
首先定义一个类,包含花费和利润。
然后建立一个花费的小根堆,一个利润的大根堆。为了后续花最少的钱赚更多的钱
然后依次将花费表和利润表放入小根堆里去。
然后根据最多做的项目数量来进行循环,在小根堆不为空的情况下把所有买得起的全扔进利润大根堆里面去。
然后进行资金的累加,将大根堆第一个的利润直接加到初始资金上。
有一个边界考虑,当大根堆为空的时候,然后还没有达到做大次数,这个时候就说明了钱不够,再怎么样也做不完所有项目,所以直接返回当前的资金就可以了
class Node { public: Node(int p,int c):profit(p),cost(c){} int cost; int profit; }; int findMaximizedCapital(int k, int w, int profits[], int capital[],int len) { priority_queue<Node*,vector<Node*>,greater<Node*>> minCostQ;//小根堆 priority_queue<Node*,vector<Node*>,less<Node*>>maxProfitQ;//大根堆 for (int i = 0; i < len; i++) { minCostQ.push(new Node(profits[i], capital[i])); } for (int i = 1; i <= k; i++) { while (!minCostQ.empty() && minCostQ.top()->cost <= w) { maxProfitQ.push(minCostQ.top()); minCostQ.pop(); } if (maxProfitQ.empty()) { return w; } w += maxProfitQ.top()->profit; maxProfitQ.pop(); } return w; }
取中位数问题
一个数据流中,随时可以取得中位数
思路:
用一个小根堆和一个大根堆进行不断的比较交换,最后获得中位数。
第一个值直接进大根堆,剩下的值如果是小于等于大根堆的堆顶,就进入大根堆,否则进入小根堆。
我画了一个图来表明上面的这个操作,我用的队列来画的图,这个不是堆的图。只是为了看的更加直观。
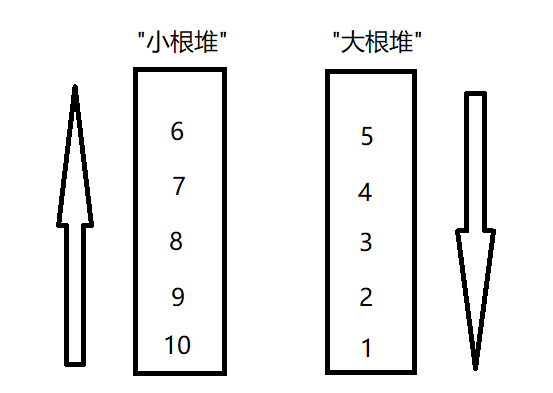
从这个图可以很直观的看出来,比大根堆小的值就让他沉下去,比大根堆堆顶大的值就放入小根堆然后让他沉下去。
相当于两个极端,一大一小都沉下去,堆顶就是中间的部分。
如果当大根堆或者小根堆里面的元素个数相差2个,就从元素多的那个堆中顶部取一个值放入元素少的那个堆中。
最后判断两个堆中的元素个数是否一样,如果一样就两个顶部相加除2。
如果不一样,就直接取元素多的那个堆的顶部
priority_queue<int, vector<int>, less<int>>maxHeap; priority_queue<int, vector<int>, greater<int>>minHeap; void heapChange() { if (maxHeap.size() == minHeap.size() + 2) { minHeap.push(maxHeap.top()); maxHeap.pop(); } if (minHeap.size() == maxHeap.size() + 2) { maxHeap.push(minHeap.top()); minHeap.pop(); } } void addNumber(int num) { if (maxHeap.empty() || num <= maxHeap.top()) { maxHeap.push(num); } else minHeap.push(num); heapChange(); } int getMid() { int maxSize = maxHeap.size(); int minSize = minHeap.size(); if (maxSize == 0 && minSize == 0) { return 0; } int minHeapHead = minHeap.top(); int maxHeadHead = maxHeap.top(); if (maxSize == minSize) { return (minHeapHead + maxHeadHead) >> 1; } return maxSize > minSize ? maxHeadHead : minHeapHead; }
字典序最小问题
给定长度为N的字符串S,要构造一个长度为N的字符串T。起初,T是一个空串,随后反复进行下列任意操作。
从S的头部删除一个字符,加到T的尾部,从S的尾部删除一个字符,加到T的尾部
目标是要构造字典序尽可能小的字符串T
思路:
从左往右的模型,定义两个变量L和R,分别等于0和字符串长度-1
当L小于等于R的时候进行循环,定义一个标志,默认为左边小,如果左边字符等于右边字符不变。
当L加上 i 小于等于 R的时候,判断 L+ i 是否小于R,如果小于 标志位改为true,如果大于 标志位改成 false
最后如果标志位是true 就打印左边的字符,如果是false就打印右边的字符。如果左右两边字符一样,标志位没有改变,输出任意字符都可以
int N = 6; string str = "abcdbc"; void solve() { int L = 0, R = N - 1; bool left = false; while (L <= R) { for (int i = 0; L + i < R; i++) { //如果首字符小于尾字符就打印首字符 if (str[L + i] < str[R - i]) { left = true; break; } else if (str[L + i] > str[R - i]) { left = false; break; } } if (left) { cout << str[L++]; } else cout << str[R--]; } }
汉诺塔问题
思路:
假设三根柱子,分别为a,b,c,当只有a只有一层的时候,直接从a移到c就可以了
当如果有n层的时候,a要想移到c,得把a上面n-1层都先移到b柱子上放着,才能把a最底层移到c去
n-1都移到了b柱子上后,还是得把b柱子上的n-1层移到另一个与目的c柱子无关的柱子上去,所以把b上面的n-1移到a上去,然后再把最后一层从b移到c
void process(int n, char from, char to, char other) { if (n == 1) { cout << from << "->" << other << endl; } else if (n > 1) { process(n - 1, from, other, to); cout << from << "->" << other << endl; process(n - 1, other, to, from); } }
打印字符串的全部子序列
打印一个字符串的全部子序列,包括空字符串
思路:
核心是用列表来装子序列,最后打印结果。
首先传入一个字符串,然后进行是否为空的判断,然后调用process递归
参数为原字符串,下标从0开始,走过的路径path默认为空串,答案列表容器ans
如果坐标index等于字符串的长度,就是说明已经到尾了,直接将路径传入答案列表中。
当还没到末尾的时候,就进行下标的加1,然后两个递归。
第一个递归是不选择当前字符,第二个递归是选择当前字符,并把当前字符加到路径上。
最后递归结束之后返回ans给main函数,打印ans容器,出来的结果是有重复的子序列。
void process(string str, int index, string path, list<string>& ans) { if (index==str.length()) { ans.push_back(path); } else { process(str, index + 1, path, ans); process(str, index + 1, path + str[index], ans); } } list<string>* allSubseq(string str) { list<string>*ans = new list<string>; if (str.empty()) { return ans; } if (str.length() == 0) { ans->push_back(""); return ans; } process(str, 0, "", *ans); return ans; }
打印字符串全排列(有重复)
打印一个字符串的全部排列
思路:
首先将数组里面的字符串放入到vector容器中,然后进行递归操作。
先判断容器中是否为空,如果为空说明路径已经搜集完了,将路径放入答案列表中。
//全排列有重复 void process(vector<char>&set, string path, list<string>& ans) { if (set.empty()) { ans.push_back(path); return; } for (int index = 0; index < set.size(); index++) { string pick = path + set[index]; vector<char>next; next.assign(set.begin(), set.end()); auto del = next.begin() + index; next.erase(del); process(next, pick, ans); } } list<string>* allSort(string str) { list<string>* ans = new list<string>; vector<char> set; for (int i = 0; i < str.length(); i++) { set.push_back(str[i]); } process2(set, "", *ans); return ans; }
打印字符串全排列(无重复)
打印一个字符串的全部排列,要求不要出现重复的排列
思路:
首先因为需要排列,所以将字符串弄到vector容器中装着,然后调用函数process进行递归。
传入参数,装字符串的容器,路径以及空的答案列表容器
当字符容器中为空的时候,代表路径已经形成,直接将路径传入ans容器中就可以了
如果不为空,就先建立一个无序表来避免重复的元素
然后进行字符容器的遍历,如果当前字符在无序表中没有就把当前字符加入无序表,并且路径上添加当前字符
然后再用临时的一个字符容器把原来的字符容器的值全拷贝,并且把当前字符删掉,从下一个字符开始,然后用临时容器作为递归参数。
//全排列无重复 void process2(vector<char>&set, string path, list<string>&ans) { if (set.empty()) { ans.push_back(path); return; } unordered_set<char> picks; for (int index = 0; index < set.size(); index++) { if (!picks.count(set[index])) { picks.insert(set[index]); string pick = path + set[index]; vector<char> next; next.assign(set.begin(), set.end()); auto del = next.begin() + index; next.erase(del); process2(next, pick, ans); } } } list<string>* allSort(string str) { list<string>* ans = new list<string>; vector<char> set; for (int i = 0; i < str.length(); i++) { set.push_back(str[i]); } process2(set, "", *ans); return ans; }
数字转字符串
规定1和A对应、2和B对应、3和C对应... 那么一个数字字符串比如"111",就可以转化为"AAA"、"KA"和"AK"。 给定一个只有数字字符组成的字符串str,返回有多少种转化结果
思路:
首先传入数字字符串,然后进行一个空串的判断,再进行process函数的调用。
终止条件,当下标i等于长度的时候,这时候就为一个有效的结果,返回1
如果当前数字字符为0,就说明当前字符不能决定是否要不要,直接返回0
当前字符为1开头的时候,得到一种结果,然后看字符串的下一个是否存在,如果存在就直接结果累加。
当前字符为2开头的时候,因为是26个字符,所以判断第二个字符是否有效的时候要加上限定,第二个字符是否在0到6之间。
最后外层的返回调用是指3至9的单个字符,不是1开头也不是2开头
int process(string str, int i) { if (i == str.length()) { return 1; } if (str[i] == '0') { return 0; } if (str[i] == '1') { int res = process(str, i + 1); if (i + 1 < str.length()) { res += process(str, i + 2); } return res; } if (str[i] == '2') { int res = process(str, i + 1); if (i + 1 < str.length() && str[i + 1] >= '0'&&str[i + 1] <= '6') { res += process(str, i + 2); } return res; } return process(str, i + 1); } int number(string str) { if (str == "" || str.length() == 0) { return 0; } return process(str, 0); }
背包问题
给定两个长度都为N的数组weights和values,weights[i]和values[i]分别代表 i号物品的重量和价值。给定一个正数bag,表示一个载重bag的袋子,你装的物 品不能超过这个重量。返回你能装下最多的价值是多少?
思路1:
传参分别是 weight 装重量的容器,value 装价值的容器,alreadyW 已经有的重量,bag 包的能装的重量大小
终止条件是已有的重量大于包能承受的重量
用两个递归解决,p1 的意思是不加当前重量的递归,p2next 是加下一个重量的递归
在这里使用一个p2next目的是为了防止下一个重量不存在,如果不存在p2next的值会变成-1
然后进行判断,当下一个重量存在的时候,就形成p2
最后进行比较最大值返回 p1不要当前货物形成的最大价值,p2要当前货物形成的最大价值
int process(vector<int>& w, vector<int>& v, int index, int alreadyW, int bag) { if (alreadyW > bag) { return -1; } if (index == w.size()) { return 0; } int p1 = process(w, v, index + 1, alreadyW, bag); int p2next = process(w, v, index + 1, alreadyW + w[index], bag); int p2 = -1; if (p2next != -1) { p2 = v[index] + p2next; } return max(p1, p2); } int maxValue(vector<int> w, vector<int> v, int bag) { return process(w, v, 0, 0, bag); }
思路2:
传参分别是 weight 重量,value 价值,rest 剩余空间
当剩余空间小于或者等于0时,或者 下标走到最后的位置的时候,直接返回0
p1 是不要当前货物进行的递归,当剩余空间大于等于当前的重量的时候,用p2 得到要当前货物的最大价值,后面process里面 rest - w[index] 是把剩余空间减去了当前货物的重量
最后再求p1 和 p2 的最大值
int process(vector<int> w, vector<int> v,int index, int rest) { if (rest <= 0) { return 0; } if (index == w.size()) { return 0; } int p1 = process(w, v, index + 1, rest); int p2 = -1; if (rest >= w[index]) { p2 = v[index] + process(w, v, index + 1, rest - w[index]); } return max(p1, p2); } int maxValue(vector<int> w, vector<int> v, int bag) { return process(w, v, 0, bag); }
纸牌问题
给定一个整型数组arr,代表数值不同的纸牌排成一条线。玩家A和玩家B依次拿走每张纸 牌,规定玩家A先拿,玩家B后拿,但是每个玩家每次只能拿走最左或最右的纸牌,玩家A 和玩家B都绝顶聪明。请返回最后获胜者的分数。 【举例】 arr=[1,2,100,4]。 开始时,玩家A只能拿走1或4。如果开始时玩家A拿走1,则排列变为[2,100,4],接下来 玩家 B可以拿走2或4,然后继续轮到玩家A... 如果开始时玩家A拿走4,则排列变为[1,2,100],接下来玩家B可以拿走1或100,然后继 续轮到玩家A... 玩家A作为绝顶聪明的人不会先拿4,因为拿4之后,玩家B将拿走100。所以玩家A会先拿1, 让排列变为[2,100,4],接下来玩家B不管怎么选,100都会被玩家 A拿走。玩家A会获胜, 分数为101。所以返回101。 arr=[1,100,2]。 开始时,玩家A不管拿1还是2,玩家B作为绝顶聪明的人,都会把100拿走。玩家B会获胜, 分数为100。所以返回100。
思路:
分别写了两个函数相互嵌套,f 代表 frist , s 代表 second ,先手和后手函数
首先在 f 函数中,i 代表最左边的位置,j 代表最右边的位置
如果 i 位置与 j 位置相同,代表现在只有一个值,那么就直接返回就可以了,返回 i 位置的值
先手和后手是一套过程,所以说这个过程。
写成函数应该是 当拿 i 位置上的值的时候,后手函数调用 ,s 函数的范围必然是从 i + 1位置上到 j 上,因为 i 位置的值已经被取走了。
反之,取 j 位置上的值,s 函数的范围 必然是 i 的位置 到 j - 1 的位置,因为 j 位置的值被取走了。
后手函数中里面,当 i 位置与 j 位置相等,说明只剩1个值了,后手函数拿不到这个值,所以返回 0
最后的返回最小值函数中,就直接调用先手函数取值 。
返回最小值是因为,先手必然拿最大值,剩下的只有最小值给后手拿 或者刚好与先手的值一样,如果是一样的话最大值最小值无所谓,这个不在考虑范围内。
在 s 函数中,返回 f 函数,只是为了去取值,因为第二个人取值的时候,也是像第一个人一样,去取最大值。
int s(vector<int>& array, int i, int j) { if (i == j) { return 0; } return min(f(array, i + 1, j), f(array, i, j - 1)); } int f(vector<int>& array, int i, int j) { if (i == j) { return array[i]; } return max(array[i] + s(array, i + 1, j), array[j] + s(array, i, j - 1)); }
N皇后问题
N皇后问题是指在N*N的棋盘上要摆N个皇后,要求任何两个皇后不同行、不同列, 也不在同一条斜线上。 给定一个整数n,返回n皇后的摆法有多少种。 n=1,返回1。 n=2或3,2皇后和3皇后问题无论怎么摆都不行,返回0。 n=8,返回92
思路:
用一个一维数组来表示皇后的位置,行号就是数组是下标,列号就是这个下标中的值
在过程函数process中,如果从0遍历到最后的n,则表示这是一组有效的解
在确定皇后位置的时候,首先要判断这个位置能不能使用,是否为对角线,或者与上一个皇后同列
用一个isValid函数来判断当前的位置是否有效,判断对角线相等用一个公式来表示,| y1 - x1 | = | y2 - x2 |
也就是record中的0到 i - 1 的列 减 当前列 ,在这之前的行 减 当前行 ,然后都取绝对值 。相当于就是判断是否为45°或者135°的角
如果是的话就返回false 表示当前位置不能作为皇后的位置。
如果返回为true, 表明当前位置可以作为皇后的位置,然后直接记录,再进行递归找下一个位置。
bool isValid(int record[], int i, int j) { for (int k = 0; k < i; k++) { if (record[k] == j || abs(record[k] - j) == abs(k - i)) { return false; } } return true; } int process(int i, int record[], int n) { if (i == n) { return 1; } int res = 0; for (int j = 0; j < n; j++) { if (isValid(record, i, j)) { record[i] = j; res += process(i + 1, record, n); } } return res; } int num(int n) { if (n < 0) { return 0; } int *record = new int[n]; return process(0, record, n); }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号