一、认识几个基本概念
计算机的数存储在寄存器中,称寄存器的位数为机器字长
- 有符号数:首位用来表示正负数,其余位表示数值
- 无符号数:没有符号的数,每一位都用来表示数值
- 机器数:把符号数字化的数为机器数,带符号,最高位存放正负号
- 真值:机器数实际表示的数称为真值,有正负
二、原码
原码:符号位加上真值的绝对值,即第一位0为正数,1为负数,其余位表示数值
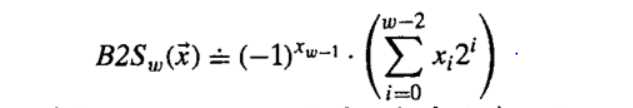
三.反码
反码:正数的反码是其本身,负数的反码是在其原码的基础上符号位不变,其余位取反;可看作除了最高位的权重是-2^(w-1)-1,其余位和补码一致
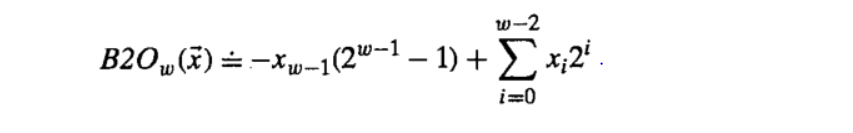
四.补码
正数的补码是其本身,负数的补码是在其原码的基础上符号位不变,其余各位取反,最后再加1,即在反码的基础上加1
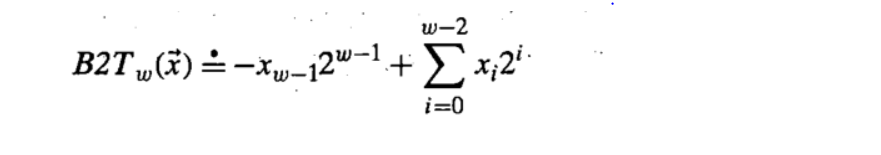
例: B2T4([1011])=-1*2^3+0*2^2+1*2^1+1*2^0=-5
补码格式对应真值的最小值:最高位为1,其余全为0时,即TMinw=-2^(w-1);当最高位为0,其余全为1,补码格式对应最大值为TMaxw=1*(1-2^(w-1))/1-2=2^(w-1)-1。即C语言数据类型中负数的范围比正数的范围大1。
计算机以补码的形式来表示数,十进制中的-1,在补码中为1111 1111,而非1000 0001
五.移码
移码:无论正数和负数,都是在其真值的基础上加一个2N,N位其位数,在数轴上移码表示的范围恰好对应于真值表示的范围向轴的正方向移动2N,所以叫为移码;不管正负数,只要将其补码的符号位取反即可得到对应的移码
移码是用来比较数的大小,正数的原码/补码/反码都相同;负数的反码是在其原码的基础上除符号位外取反,补码是在反码的基础上+1,或在原码的基础上除符号位外取反加1
六、原码、反码、补码的使用原因
计算机使用原码计算时需要辨别符号位,硬件实现起来相对复杂,为了简化,增设以上概念,将符号位带入运算,并且只保留加法
例:对简单的减法运算 1-1
原码:符号位参与运算的情况显然不对
1-1=1+(-1)=[0000 0001]+[1000 0001]=[1000 0010]=-2
这里引入反码来计算减法:
1-1=1+(-1)=[0000 0001]原+[1000 0001]原=[0000 0001]反+[1111 1110]反=[1111 1111]反=[1000 0000]原=0
真值部分是正确的,但是0的符号位为1或者是0,两个编码表示一个数字,存在争议,0带符号是没有意义的,所以引入补码:恰好解决了0的问题和两个编码表示一个数字的问题。且可以表示原码和反码里不能表示的-128,存储的数值范围是[-2N-1,2N-1-1],原码反码范围[-2N-1-1,2N-1-1],程序中注意越界问题。
1-1=1+(-1)=[0000 0001]原+[1000 0001]原=[0000 0001]补+[1111 1111]补=[0000 0000]补=[0000 0000]原
(-1)+(-127)=[1000 0001]原+[1111 1111]原=[1111 1111]补+[1000 0001]补=[1000 0000]补
七.深入
1.同余的概念:
两整数a,b,若它们除以整数m所得余数相等,则a,b对于模m同余,记作a≡b(mod m);即a与b关于模m同余
2.负数取模:x mod y,即求x除以y的余数,等于x减去y乘以x与y的商的下界
x mod y =x-y*(x/y的下界);例: -3 mod 2=-3-2*(-3/2的下界)=-3-2*(-2)=4-3=1
3.同余数的反身性:
a≡a(mod m)
同余数的线性运算定理
若 a ≡ b (mod m),c ≡ d (mod m) 则有:(1)a ± c ≡ b ± d (mod m) ;(2)a * c ≡ b * d (mod m)
4.一个数的反码,实际上就是这个数对于一个膜的同余数,这个模就是对应二进制位数所能表示的最大值,相当于127个刻度转一轮,变减法为加法;
补码也能参与运算的原因:在反码的基础桑,增加了模的值,相当于每128个刻度转一轮。
八.有符号数和无符号数之间的转换
计算机在解释一个数据类型的值主要有4个因素:位排列规则(大端或者小端),起始位置,数据类型的字节数,数据类型的解释方式。特定系统前两种因素是特定的。强制类型转换,即改变后两种因素,可以改变一个数据类型的最终计算结果。
①有符号数转为无符号数
补码转换成无符号编码时,先将补码编码转换成二进制序列,再将二进制序列转换成无符号编码。即:
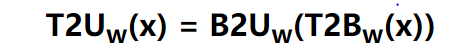
1.将无符号编码和补码编码的公式相减,0-(w-2)位的加权和相互抵消
B2Uw(X)-B2Tw(X)=Xw-1*2^(w-1) - (-Xw-1*2^(w-1))=Xw-1*2^w
2.将等式左边的B2Tw(X)移到等式右边
B2Uw(X)=Xw-1*2^w+B2Tw(X)
3.令X为T2Bw(X)
B2Uw(T2Bw(X))=Xw*2^w+B2Tw(T2Bw(X))=Xw-1*2^w+X;
即 T2Uw(X)=Xw-1*2^w+X
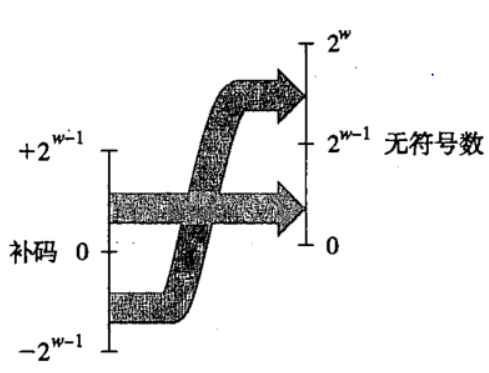
对有符号数的补码形式,最高位为0,即Xw=0,其对应无符号数是其本身,当最高位为1,即X为负数,Xw-1=1,其无符号数为X+2w;即当一个有符号数映射为它相应的无符号数时,负数被转换成了大的正数,非负数则保持不变,得到的无符号数范围为0=<X<2^w;
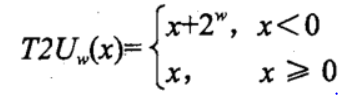
②无符号数转换成有符号数
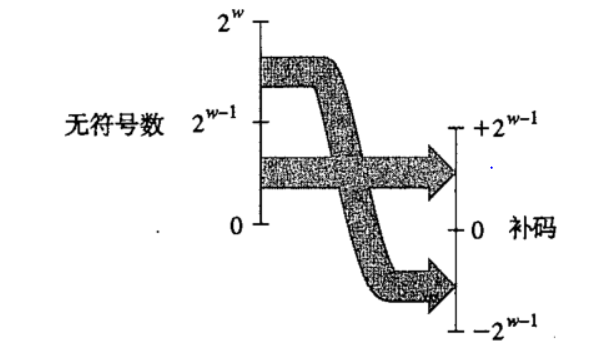
刚好是相反的过程。
C语言当执行一个运算,会隐式的将有符号数强制转换为无符号数,要注意实际编码过程种由于隐式转换所造成的错误运算
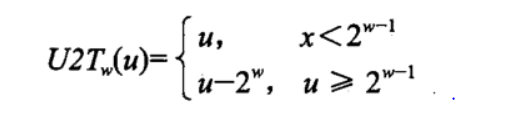
九.数位的拓展
即在不同字长的整数间转换,需要保持前后的数值不变,一个数据转换成字长更小的数据类型时,它的值肯定会发生变化,所以只能将较小的数据类型转换成较大的数据类型。
原始位为[a,b,c,……d,e,f,g],扩展后成为[a,a,a,a……,a,b,c,……d,e,f,g]
①将一个无符号数转换成一个更大的数据类型,只需简单的在二进制序列前添加0即可
②将补码数字转换成更大的数据类型,需要在开头添加符号位
证明:B2Tw+k([Xw-1,Xw-1,Xw-1,Xw-2,……,X1,X0])=B2Tw([Xw-1,Xw-1……X1,X0])
若能正能扩展一位值是不变的,那么就可以说明扩展多少位值不变都是成立的
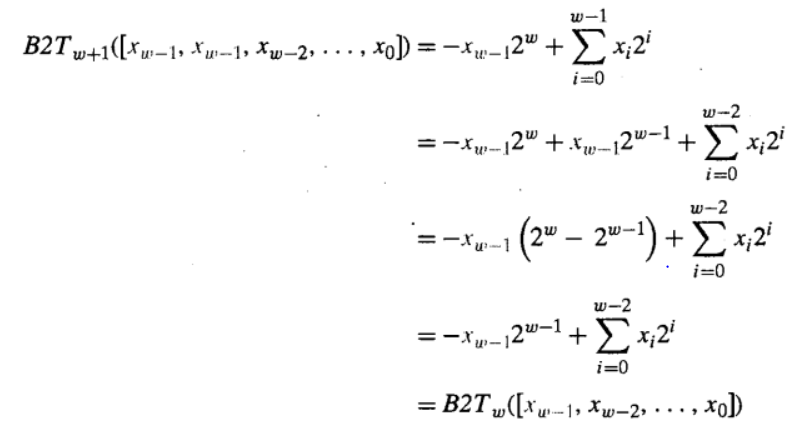
即证明完毕。
十.数位的截断
即减少一个数字的位数:将一个w位的截断成一个k位的数字,将丢弃高w-k位
①对无符号数的截断
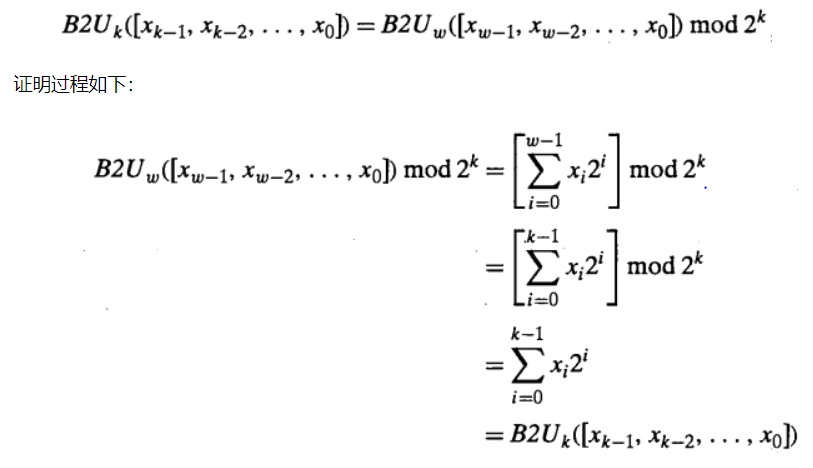
②对于有符号数的截断为:将无符号编码转换成补码编码即可
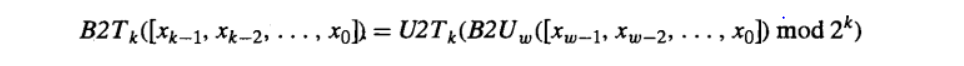



 浙公网安备 33010602011771号
浙公网安备 33010602011771号