寻找第k大树

 

 

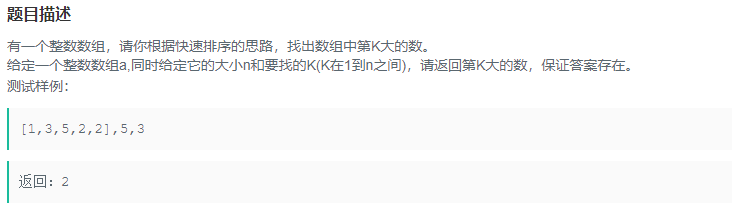
 方法一：

将整个数组进行排序，可使用快排，时间复杂度O(nlogn)，这是一个可行的方法，但是还可以优化

所以代码略，如果想偷懒，使用util包提供的函数，就两行代码，Arrays.sort(a);return a[n-k];

方法二：

分析一下快速排序会发现，每一次排序后都能找到第 i+1（i=j时返回i）大的元素

若i-left+1比K更大，就说明需要找的数在[left,i-1]之间

若i-left+1比K更小，就说明需要找的数在[i+1,right]之间，注意，这里因为已经找到了前i-left+1大的数，所以还需要再[i+1,right]

空间里找到前K-(i-left+1)大的数，故K-=(i-left+1);

若i-left+1==K,放回a[i];

以下是进行快速排序的一个步骤：

 1 private int AdjustArray(int [] a,int l,int r){//快速排序的一个子步骤
 2         int i = l,j = r;
 3         int x = a[l];
 4         while(i < j){
 5             while(i < j && a[j] <= x){
 6                 j--;
 7             }
 8             if(i < j){
 9                 a[i] = a[j];
10                 i++;
11             }
12             while(i < j && a[i] > x){
13                 i++;
14             }
15             if(i < j){
16                 a[j] = a[i];
17                 j--;
18             }
19         }
20         a[i] = x;
21         return i; 
22     }
View Code

分治的代码

 1 public int findKth(int[] a, int n, int K) {
 2         // write code here
 3         int left = 0,right = n-1;
 4         int i = -1;
 5         while((i - left) != K - 1){
 6             i = AdjustArray(a,left,right);
 7             if((i - left) == (K - 1)){
 8                 return a[i];
 9             }else if((i - left) < (K - 1)){
10                 K = K - (i - left) - 1;
11                 left = i + 1;
12             }else if((i - left) > (K - 1)){
13                 right = i - 1;
14             }
15         }
16         return -1;
17     }
View Code

代码合体：

 1 import java.util.*;
 2 
 3 public class Finder {
 4     private int AdjustArray(int [] a,int l,int r){//快速排序的一个子步骤
 5         int i = l,j = r;
 6         int x = a[l];
 7         while(i < j){
 8             while(i < j && a[j] <= x){
 9                 j--;
10             }
11             if(i < j){
12                 a[i] = a[j];
13                 i++;
14             }
15             while(i < j && a[i] > x){
16                 i++;
17             }
18             if(i < j){
19                 a[j] = a[i];
20                 j--;
21             }
22         }
23         a[i] = x;
24         return i; 
25     }
26     public int findKth(int[] a, int n, int K) {
27         // write code here
28         int left = 0,right = n-1;
29         int i = -1;
30         while((i - left) != K - 1){
31             i = AdjustArray(a,left,right);
32             if((i - left) == (K - 1)){
33                 return a[i];
34             }else if((i - left) < (K - 1)){
35                 K = K - (i - left) - 1;
36                 left = i + 1;
37             }else if((i - left) > (K - 1)){
38                 right = i - 1;
39             }
40         }
41         return -1;
42     }
43 }
View Code

方法二与方法一的区别在于方法二不会对整个数组进行排序，时间复杂度为O(n)!

posted @ 2020-08-25 22:03  雨下_整夜  阅读(199)  评论(0)    收藏  举报