DLX学习笔记

题

简化题意：精确覆盖问题

\(Sol\)

于是只要我们有了一个能加点，删竖列，添竖列，删横行，添横行能递归寻找是否存在解并能保存解的结构即可

scanf("%d%d",&n,&m);
DLX.init(n,m);
for(int i=1;i<=n;i++) for(int j=1;j<=m;j++){
	scanf("%d",&x); if(x) DLX.ins(i,j);
}
if(DLX.dance(1)) for(int i=1;i<=p;i++)
	printf("%d ",ans[i]);
else puts("No Solution!");

于是先把主程序架构好，接下来要写这种神奇的结构了

初始化：

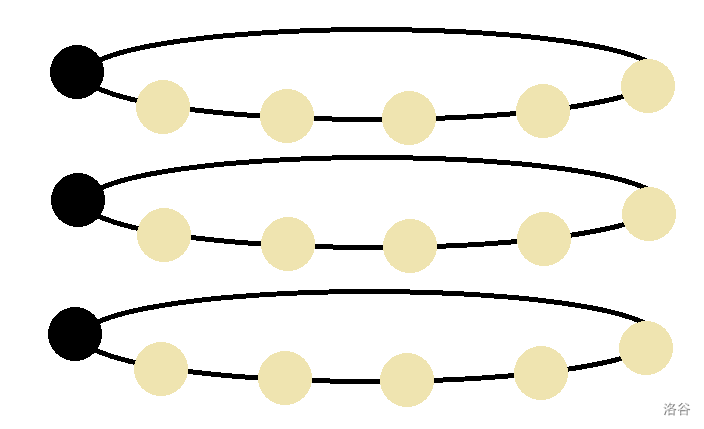
黑点是 \(0\)

加点：

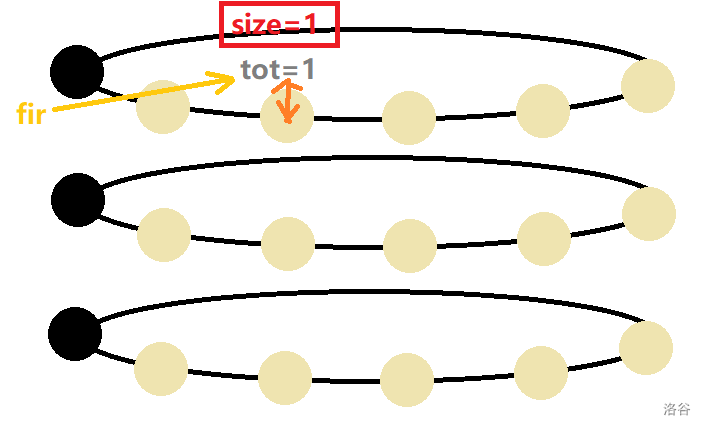
\(10\) \(years\) \(later:\)

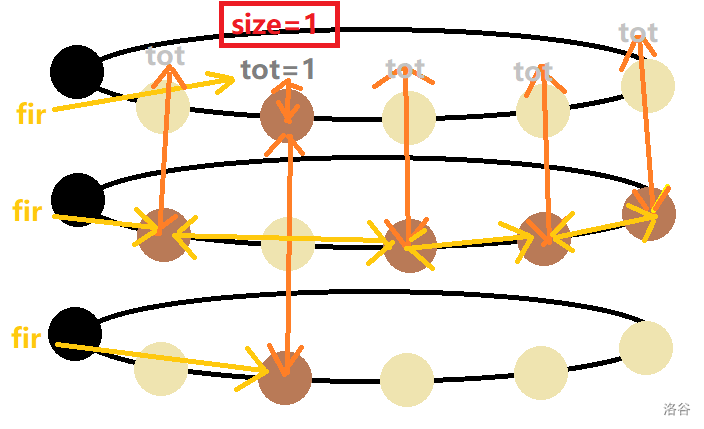
每个点会有不同的标号，包括 \(tot\) ，\(fir\) 数组指当前一排的一个点

当然，每排最右边的也连最左边的，画上去就太乱了

褐色是题中值为 \(1\) 的点

\(\operatorname{del}\) 和 \(\operatorname{rec}\) 不讲

接下来开始跳舞了

找到成员最少的列，枚举它每位成员在的行，模拟删掉，看最后行不行

练习题

完结撒花~