凸包学习笔记
2022/3/11 Update:学会了叉积,来改一下以前瞎逼逼的,不知道是什么东西的东西
以这道为例题
简化题意:给出 \(n\) 个点的坐标,问最小的多边形的周长,满足 \(n\) 个点都被他包含(边上也算)
我直接开讲 \(\texttt{Graham}\) 吧
现在我们有一张图:

开始给出的点没有顺序,我们首先需要找一种处理的顺序
我们从最下面的点开始好了
容易想到一种排序方式,把最下面的点与其他点连边,就像这样:
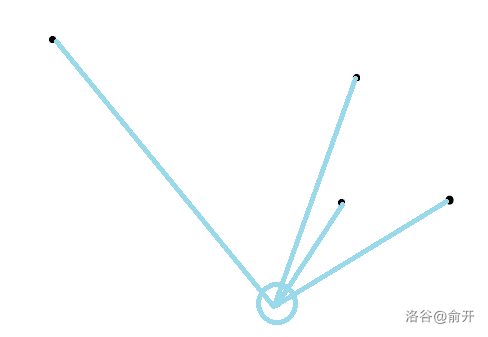
图略丑误喷
然后从右往左处理每个点
排序部分的代码实现:
bool cmp(node p1,node p2){
db tmp=check(p[1],p1,p[1],p2);
if(tmp>0 ||(tmp==0 && dis(p[0],p1)<dis(p[0],p2))) return 1;
return 0;
}
接下来就是具体如何处理了
二话不说先放图:

第一条连边,没什么好说的
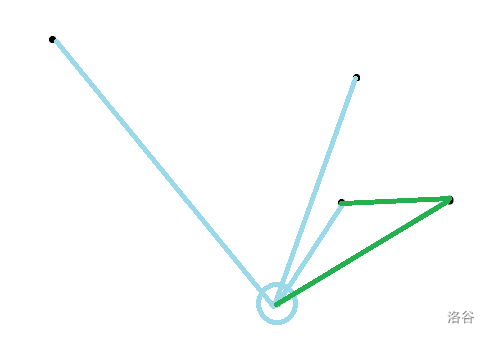
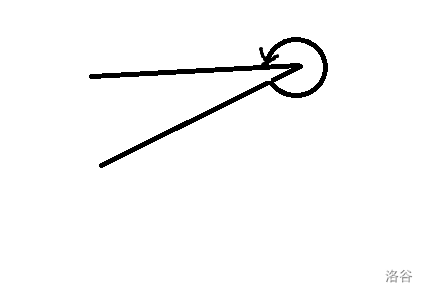
第二条,夹角超过180度,显然符合
哦我说的是这个角
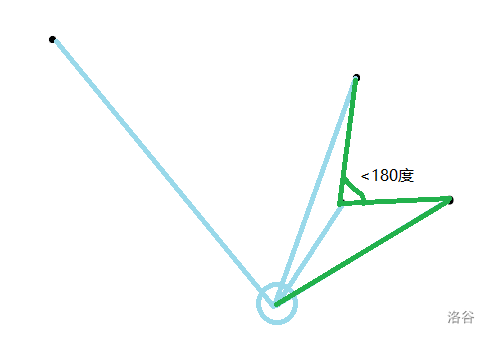
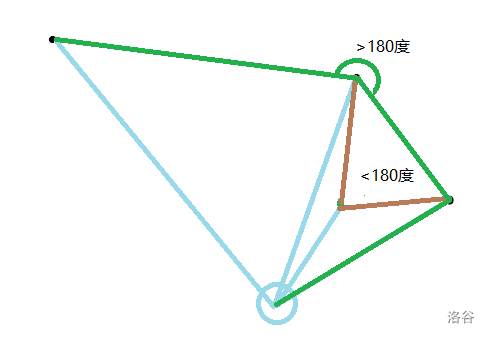
好,问题来了现在相邻的边的夹角<180度了,此时显然有一种更优的情况:
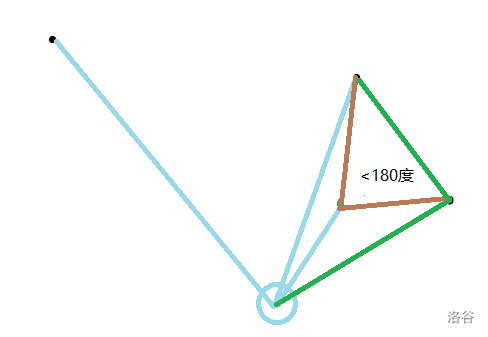
褐色的太逊了,被淘汰了
接下来没什么事了
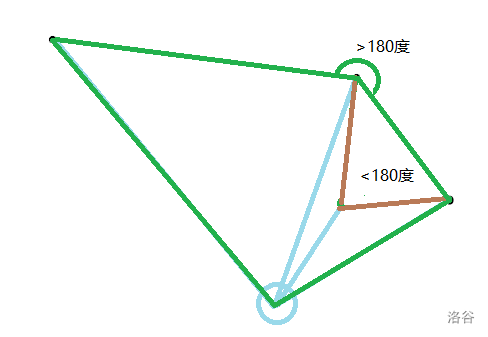
凸包画(吐)完辣!
于是得出这部分的代码:
tb[1]=p[1];
int cnt=1;
for(int i=2;i<=n;i++){
while(cnt>1&&check(tb[cnt-1],tb[cnt],tb[cnt],p[i])<=0) cnt--;
tb[++cnt]=p[i];
}
哦对了,两段代码里都用到的 \(\operatorname{check}\) 函数什么呢
Upd:那时我好逊,为什么取名叫\(check\)不叫\(cross\)
db check(node a1,node a2,node b1,node b2){
return (a2.x-a1.x)*(b2.y-b1.y)-(b2.x-b1.x)*(a2.y-a1.y);
}
还是先贴代码,这个柿子正负值表示的含义(可以死记)可以推
斜率想必大家都知道,
\(k_{\overrightarrow{a_1a_2}}=({a_2}_y-{a_1}_y)/({a_2}_x-{a_1}_x)\)
\(k_{\overrightarrow{b_1b_2}}=({b_2}_y-{b_1}_y)/({b_2}_x-{b_1}_x)\)
在 \(sort\) 的 \(check\) 中,\(check\)用于比较两个点分别与\(p_1\) 连起来后线段的先后顺序
于是有这两种情况:
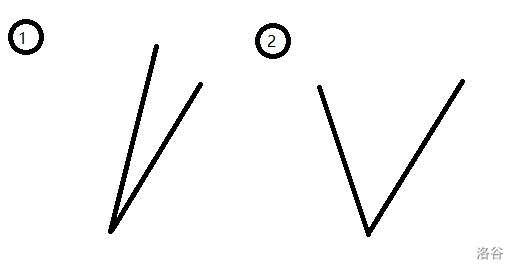
于是,当\(({a_2}_x-{a_1}_x)\)
和
\(({b_2}_x-{b_1}_x)>0\)
时
\(k_{\overrightarrow{a_1a_2}}-k_{\overrightarrow{b_1b_2}}\)
\(=({a_2}_y-{a_1}_y)/({a_2}_x-{a_1}_x)-({b_2}_y-{b_1}_y)/({b_2}_x-{b_1}_x)\)
与
\(({a_2}_y-{a_1}_y)*({b_2}_x-{b_1}_x)-({b_2}_y-{b_1}_y)*({a_2}_x-{a_1}_x)\)
同号
即\(k_{\overrightarrow{b_1b_2}}-k_{\overrightarrow{a_1a_2}}\)
与
\(({b_2}_y-{b_1}_y)*({a_2}_x-{a_1}_x)-({a_2}_y-{a_1}_y)*({b_2}_x-{b_1}_x)\)
同号,
于是这个柿子 \(>0\) 的意义是 \(k_{\overrightarrow{b_1b_2}}-k_{\overrightarrow{a_1a_2}}>0\)
即后者的斜率比前者大,于是这部分排序后顺序就该是这样
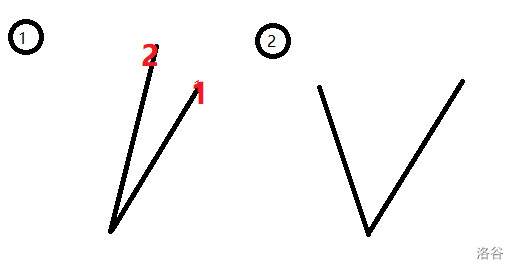
啊哈,排对了
对于 \(2\) 的话
\(({b_2}_y-{b_1}_y)*({a_2}_x-{a_1}_x)-({a_2}_y-{a_1}_y)*({b_2}_x-{b_1}_x)\)
中
\(({b_2}_y-{b_1}_y)*({a_2}_x-{a_1}_x)>0\)
\(({a_2}_y-{a_1}_y)*({b_2}_x-{b_1}_x)<0\)
于是
\(({b_2}_y-{b_1}_y)*({a_2}_x-{a_1}_x)-({a_2}_y-{a_1}_y)*({b_2}_x-{b_1}_x)>0\)
按照这个顺序:

还有一种情况刚才忘了
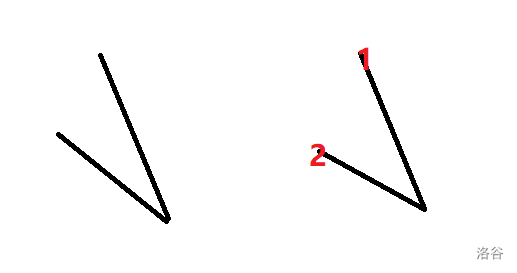
也易证,顺序是对的
以上是排序时 \(\operatorname{check}\) 的用法
接下来是取凸包点时 \(\operatorname{check}\) 的用法
将会有以下几种情况:

是符合条件的, \(\operatorname{check}\) 值 \(>0\)
读者自证不难
Upd:不就是我那时候不会吗,根本不用分讨,用叉积的性质解决一切问题 Click Here
剩下的,不符合的删干净,最后就能得到完整的凸包,代码上边已经放过了
做到这里,这道题剩下部分小问题了吧,求每两个相邻点的欧氏距离,相加即为周长
这里放一下完整的代码:
#include<bits/stdc++.h>
#define db double
using namespace std;
const int M=1e5+7;
int n; db ans;
struct node{
db x,y;
}p[M],tb[M];
db check(node a1,node a2,node b1,node b2){
return (a2.x-a1.x)*(b2.y-b1.y)-(b2.x-b1.x)*(a2.y-a1.y);
//<0表右转 =0表共线 >0表左转
}
db dis(node p1,node p2){
return sqrt((p2.y-p1.y)*(p2.y-p1.y)+(p2.x-p1.x)*(p2.x-p1.x));
}
bool cmp(node p1,node p2){
db tmp=check(p[1],p1,p[1],p2);
if(tmp>0 ||(tmp==0 && dis(p[0],p1)<dis(p[0],p2))) return 1;
return 0;
}
int main(){
scanf("%d",&n);
for(int i=1;i<=n;i++){
scanf("%lf%lf",&p[i].x,&p[i].y);
if(i!=1&&(p[i].y<p[1].y ||(p[i].y==p[1].y && p[i].x<p[1].x)))
swap(p[1],p[i]);
}
sort(p+2,p+1+n,cmp),tb[1]=p[1];
int cnt=1;
for(int i=2;i<=n;i++){
while(cnt>1&&check(tb[cnt-1],tb[cnt],tb[cnt],p[i])<=0) cnt--;
tb[++cnt]=p[i];
}
for(int i=1;i<=cnt;i++) ans+=dis(tb[i],tb[i%cnt+1]);
printf("%.2lf\n",ans);
return 0;
}
完结撒花~
你觉得对你有帮助的话,请不要吝啬您手中的赞
如果有讲得不清楚的地方,或讲错的地方,欢迎在讨论区打脸



 浙公网安备 33010602011771号
浙公网安备 33010602011771号