leetcode题目142.环形链表Ⅱ(中等)
题目描述:
给定一个链表,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。
为了表示给定链表中的环,我们使用整数 pos 来表示链表尾连接到链表中的位置(索引从 0 开始)。 如果 pos 是 -1,则在该链表中没有环。
说明:不允许修改给定的链表。
示例 1: 输入:head = [3,2,0,-4], pos = 1 输出:tail connects to node index 1 解释:链表中有一个环,其尾部连接到第二个节点。
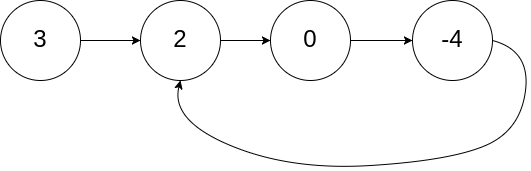
示例 2: 输入:head = [1,2], pos = 0 输出:tail connects to node index 0 解释:链表中有一个环,其尾部连接到第一个节点。

示例 3: 输入:head = [1], pos = -1 输出:no cycle 解释:链表中没有环。

进阶:
你是否可以不用额外空间解决此题?
思路分析:
思路一: 哈希, 空间复杂度O(n)O(n)
这个很好考虑, 把遍历过的节点记录,当发现遍历的节点下一个节点遍历过, 返回它
public class Solution {
public ListNode detectCycle(ListNode head) {
Set<ListNode> lookup = new HashSet<>();
ListNode p = head;
while (p != null) {
lookup.add(p);
if (lookup.contains(p.next)) return p.next;
p = p.next;
}
return null;
}
}
思路二 : 快慢指针(题解来自@paocai大神:https://leetcode-cn.com/u/powcai/)
说一下算法思路:
先用快慢指针, 找到他们相遇点(如果存在环)
再重新从链表头开始, 以及步骤1的相遇点, 两个位置一起走, 再次相遇就是环的入口
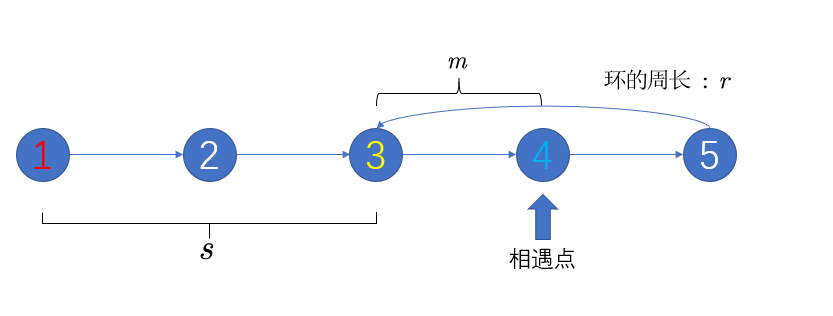
有三个节点需要注意: 起始节点(head), 环的入口节点(输出结果), 相遇的节点(快慢指针求的)
我们要证明 : 初始点到环的入口的步数 等于 相遇点到环入口的步数
我们令, 初始点到入口为 s, 入口到相遇点 m, 环的周长为 r
我们只需证明: s == r - m
首先我们假设,慢指针走了 k 步到相遇点, 那么快指针就是 2k 步,所以我们有 2k - k = nr 即 k = nr(慢指针还没到环,快指针已经转了好几圈)
还有, s = k - m
得 : s = nr - m ==> s == (n - 1) r + (r - m)
得证!
public class Solution {
public ListNode detectCycle(ListNode head) {
if (head == null || head.next == null) return null;
ListNode slow = head;
ListNode fast = head;
ListNode start = head;
while (fast != null && fast.next != null) {
slow = slow.next;
fast = fast.next.next;
if (slow == fast) {
while (start != slow) {
slow = slow.next;
start = start.next;
}
return slow;
}
}
return null;
}
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号