CSP-S算法精选营
数据结构
堆

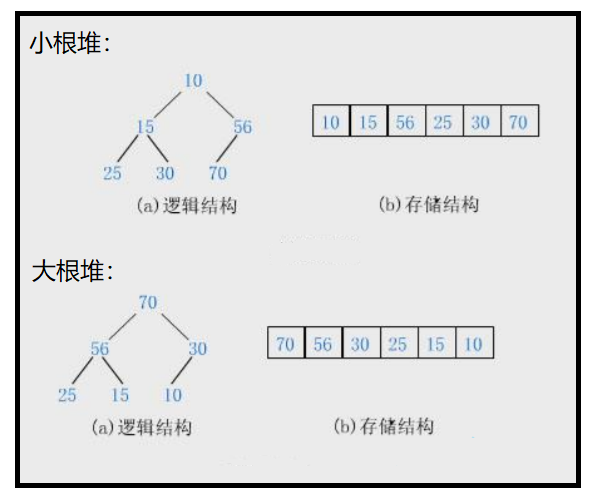
大根堆
定义:priority_queue<数据类型> 变量名
小根堆
ps:可以使用大根堆数据取相反数,也可使用priority_queue<数据类型,vector<数据类型>,greater<数据类型> >变量名;
#include<queue>
//#include<bits/stdc++.h>
using namespace std;
priority_queue<int> q;
//大根堆
//小根堆最简单的方法:取负号
struct rec
{
int a,b;
};
//如果要把结构体 放入 stl比大小 只能重载小于号
bool operator<(const rec &x,const rec &y)
{
return x.a + x.b > y.a + y.b;
}
priority_queue<rec> qq;//取出a+b最小的结构体
int main()
{
q.push(233);
q.push(2233);//向堆里面加入一个元素
q.pop();//从堆中删除一个元素 删除是堆中最大的元素 2233 void类型没有返回值
int x = q.top();//获取堆中最大元素 233
cout << q.size() << endl;//获取堆剩余的元素个数 1
}
手写堆
struct heap
{
int a[1010];//堆的每一个元素
int n=0;//堆有几个元素
int top()//询问最大值
{
return a[1];
}
void push(int x)//插入一个数
{//O(logn)
n++;a[n] = x;
int p=n;
while (p!=1)
{
if (a[p] > a[p>>1])
{
swap(a[p],a[p>>1]);
p = p>>1;
}
else
{
break;
}
}
}
void pop()//删除最大值
{
swap(a[1],a[n]);n--;
int p=1;
while ((p<<1) <= n)
{
int l=p<<1;
int r=l|1;//p*2+1
int pp=l;
if (r<=n && a[r] > a[l]) pp=r;//pp一定是两个儿子中较大的那个
if (a[pp] > a[p])
{
swap(a[pp],a[p]);
p=pp;
}
else
{
break;
}
}
}
int size()//询问还有几个数
{
return n;
}
};
并查集
引入
并查集是一种用于管理元素所属集合的数据结构,实现为一个森林,其中每棵树表示一个集合,树中的节点表示对应集合中的元素。
顾名思义,并查集支持两种操作:
合并(Union):合并两个元素所属集合(合并对应的树)
查询(Find):查询某个元素所属集合(查询对应的树的根节点),这可以用于判断两个元素是否属于同一集合
int to[maxn];//to[i] 代表i的箭头指向谁
int go(int p)//从p点出发 看最后会走到哪里
{
if (p == to[p]) return p;
else
{
to[p] = go(to[p]);
return to[p];
}
}
int main()
{
cin >> n;
for (int i=1;i<=n;i++)
to[i] = i;
//合并
to[go(p1)] = go(p2);
//查询
go(p1) == go(p2);
}
优化技巧-按秩合并
int to[maxn];//to[i] 代表i的箭头指向谁
int go(int p)//从p点出发 看最后会走到哪里
{
if (p == to[p]) return p;
else
{
to[p] = go(to[p]);
return to[p];
}
}
int main()
{
cin >> n;
for (int i=1;i<=n;i++)
to[i] = i;
//合并
if (rand()%2)
to[go(p1)] = go(p2);
else
to[go(p2)] = go(p1);
//查询
go(p1) == go(p2);
}
Trie树
定义
字典树,英文名 trie。顾名思义,就是一个像字典一样的树
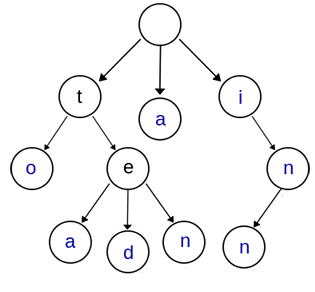
struct node
{
int nxt[2];//nxt[0] nxt[1] 代表从当前点走0和1会走到哪里 走到0的话代表这个节点不存在
node()
{
nxt[0] = nxt[1] = 0;
}
}z[23333];
void insert(int x)
{
int p=root;
for (int i=30;i>=0;i--)
{
int y=(x>>i)&1;//取出x二进制的第i位
if (z[p].nxt[y] == 0) {;
cnt++;
z[p].nxt[y] = cnt;
}
p = z[p].nxt[y];
}
}
int query(int x)//从trie中找一个数 使得他和x异或之后最大
{
int p=root,ans=0;
for (int i=30;i>=0;i--)
{
int y=(x>>i)&1;
if (z[p].nxt[y^1] != 0) ans=ans|(1<<i),p=z[p].nxt[y^1];
else p=z[p].nxt[y];
}
return ans;
}
int main()
{
root = 1;
}
分块
引入:其实,分块是一种思想,而不是一种数据结构。
分块的基本思想是,通过对原数据的适当划分,并在划分后的每一个块上预处理部分信息,从而较一般的暴力算法取得更优的时间复杂度。
例:P3372线段树1
#include <cmath>
#include <iostream>
using namespace std;
int id[50005], len;
// id 表示块的编号, len=sqrt(n) , 即上述题解中的s, sqrt的时候时间复杂度最优
long long a[50005], b[50005], s[50005];
// a 数组表示数据数组, b 数组记录每个块的整体赋值情况, 类似于 lazy_tag, s
// 表示块内元素总和
void add(int l, int r, long long x) { // 区间加法
int sid = id[l], eid = id[r];
if (sid == eid) { // 在一个块中
for (int i = l; i <= r; i++) a[i] += x, s[sid] += x;
return;
}
for (int i = l; id[i] == sid; i++) a[i] += x, s[sid] += x;
for (int i = sid + 1; i < eid; i++)
b[i] += x, s[i] += len * x; // 更新区间和数组(完整的块)
for (int i = r; id[i] == eid; i--) a[i] += x, s[eid] += x;
// 以上两行不完整的块直接简单求和,就OK
}
long long query(int l, int r, long long p) { // 区间查询
int sid = id[l], eid = id[r];
long long ans = 0;
if (sid == eid) { // 在一个块里直接暴力求和
for (int i = l; i <= r; i++) ans = (ans + a[i] + b[sid]) % p;
return ans;
}
for (int i = l; id[i] == sid; i++) ans = (ans + a[i] + b[sid]) % p;
for (int i = sid + 1; i < eid; i++) ans = (ans + s[i]) % p;
for (int i = r; id[i] == eid; i--) ans = (ans + a[i] + b[eid]) % p;
// 和上面的区间修改是一个道理
return ans;
}
int main() {
int n;
cin >> n;
len = sqrt(n); // 均值不等式可知复杂度最优为根号n
for (int i = 1; i <= n; i++) { // 题面要求
cin >> a[i];
id[i] = (i - 1) / len + 1;
s[id[i]] += a[i];
}
for (int i = 1; i <= n; i++) {
int op, l, r, c;
cin >> op >> l >> r >> c;
if (op == 0)
add(l, r, c);
else
cout << query(l, r, c + 1) << endl;
}
return 0;
}
莫队
ps:一种基于分块思想的著名离线算法
struct query
{
int l,r,id,ans;
}q[maxn];
bool cmp1(const query &q1, const query &q2)
{
if (belong[q1.l] != belong[q2.l]) return belong[q1.l] < belong[q2.l];
else return q1.r < q2.r;
}
bool cmp2(const query &q1, const query &q2)
{
return q1.id < q2.id;
}
void ins(int x)
{
cnt[x] ++;
if (cnt[x] % 2 == 0) ans++;
else if (cnt[x] != 1) ans--;
}
void del(int x)
{
cnt[x] --;
if (cnt[x] != 0)
{
if (cnt[x] % 2 == 0) ans++;
else ans--;
}
}
int main()
{
cin >> n >> m;
for (int i=1;i<=n;i++)
cin >> a[i];
for (int i=1;i<=m;i++)
{
cin >> q[i].l >> q[i].r;
q[i].id = i;
}
int s = sqrt(n);
for (int i=1;i<=n;i++)
belong[i] = i/s+1;
sort(q+1,q+m+1,cmp1);
for (int i=q[1].l;i<=q[1].r;i++)
ins(a[i]);
q[1].ans = ans;
for (int i=2;i<=m;i++)//O(Nsqrt(N))
{
int l1=q[i-1].l,r1=q[i-1].r;
int l2=q[i].l,r2=q[i].r;
if (l1 < l2)
for (int i=l1;i<l2;i++)
del(a[i]);
else
for (int i=l2;i<l1;i++)
ins(a[i]);
if (r1 < r2)
for (int i=r1+1;i<=r2;i++)
ins(a[i]);
else
for (int i=r2+1;i<=r1;i++)
del(a[i]);
q[i].ans = ans;
}
sort(q+1,q+m+1,cmp2);
for (int i=1;i<=m;i++)
cout << q[i].ans << "\n";
return 0;
}
线段树
主要是用于区间问题
形如:
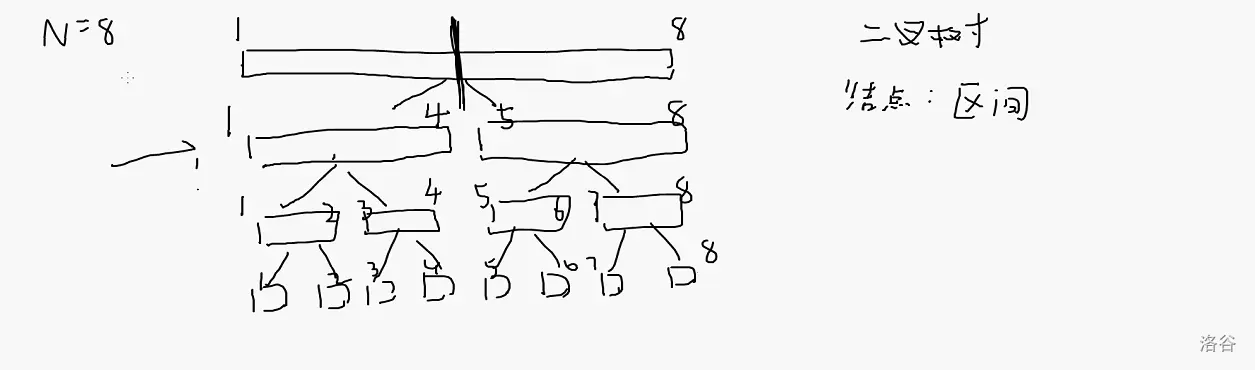
懒标记:对于线段树进行修改时,我们考虑先不对它进行修改,而是对他打上标记后,下一次询问他时在下放到部分里
#include<bits/stdc++.h>
using namespace std;
#define root 1,n,1
#define lson l,m,rt<<1
#define rson m+1,r,rt<<1|1
const int maxn=100010;
int n,m,a[maxn];
struct node//一个线段树节点
{
int sum;//代表区间和
int size;//代表区间长度
int add;//这段区间被整体加了多少
node()
{
sum = size = add = 0;
}
void init(int v)//用一个数初始化
{
sum = v;
size = 1;
}
}z[maxn<<2];//z[i]就代表线段树的第i个节点
node operator+(const node &l,const node &r)
{
node res;
res.sum = l.sum + r.sum;
res.size = l.size + r.size;
return res;
}
void color(int l,int r,int rt,int v)//给l,r,rt这个节点打一个+v的懒标记
{
z[rt].add += v;
z[rt].sum += z[rt].size * v;
}
void push_col(int l,int r,int rt)//标记下放 把标记告诉儿子
{
if (z[rt].add == 0) return; //没标记 不需要下放 可以不要这句话 但会慢些
int m=(l+r)>>1;
color(lson,z[rt].add);
color(rson,z[rt].add);
z[rt].add=0;
}
void build(int l,int r,int rt)//建树 初始化l,r,rt这个节点
//编号为rt的线段树节点 所对应的区间是l~r
{
if (l==r)
{
z[rt].init(a[l]);
return;
}
int m=(l+r) >> 1;
build(lson);
build(rson);
z[rt] = z[rt<<1] + z[rt<<1|1];
}
node query(int l,int r,int rt,int nowl,int nowr)
//l,r,rt描述了一个线段树节点
//nowl nowr代表了询问的区间的左端点和右端点
{
if (nowl <= l && r <= nowr) return z[rt];
push_col(l,r,rt);
int m=(l+r)>>1;
if (nowl<=m)
{
if (m<nowr) return query(lson,nowl,nowr) + query(rson,nowl,nowr);
else return query(lson,nowl,nowr);
}
else return query(rson,nowl,nowr);
}
void modify(int l,int r,int rt,int nowl,int nowr,int v)
//把nowl~nowr这段区间全部整体+v
{
if (nowl<=l && r<=nowr)//当前线段树节点被修改区间整体包含
{
color(l,r,rt,v);//给l,r,rt这个节点打一个+v的懒标记
return;
}
push_col(l,r,rt);
int m=(l+r)>>1;
if (nowl<=m) modify(lson,nowl,nowr,v);
if (m<nowr) modify(rson,nowl,nowr,v);
z[rt] = z[rt<<1] + z[rt<<1|1];
}
int main()
{
cin >> n;
for (int i=1;i<=n;i++)
cin >> a[i];
build(root);
cin >> m;
for (int i=1;i<=m;i++)
{
int opt;
cin >> opt;
if (opt==1)//询问
{
int l,r;
cin >> l >> r;
cout << query(root,l,r).sum << "\n";
}
else
{
int l,r,v;
cin >> l >> r >> v;
modify(root,l,r,v);
}
}
return 0;
}
可持久化数据结构
对于一个可能经过多次修改的数据结构,我们可能会需要找到他历史状态中的数据,
此时就可以用可持久化数据结构(强制在线)
可持久化数组
可以使用
pair<pair<int,int>,int> 变量名
来实现,三个值分别代表位置,时间,值
可持久化线段树
对于每次经过修改的线段树(单点修改),有且仅有一条链与原线段树不同,
我们考虑只把不同的地方建出来,剩下的直接Ctrl+c复制过去
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int MAXN = 1e5 + 7;
int read()
{
int x = 0, w = 1;
char ch = getchar();
while(ch > '9' || ch < '0')
{
if(ch == '-')
{
w = -1;
ch = getchar();
}
}
while(ch <= '9' && ch >= '0')
{
x = x * 10 + ch - '0';
ch = getchar();
}
return x * w;
}
long long Qmi(int a, int b, int p)
{
if(b == 0)
{
return 1%p;
}
if(b == 1)
{
return a%p;
}
long long ans = Qmi(a, b/2, p);
ans = ans*ans%p;
if(b % 2)
{
ans = ans*a%p;
}
return ans % p;
}
bool isprime(long long x)
{
if(x <= 1)
{
return false;
}
if(x == 2)
{
return true;
}
if(x % 2 == 0)
{
return false;
}
for(int i = 3; i <= sqrt(x); i += 2)
{
if(x % i == 0)
{
return false;
}
}
return true;
}
int cnt;
int a[MAXN], root[MAXN];
struct node
{
int l, r;
int sum;
node()
{
l = r = sum = 0;
}
}z[MAXN*20];//应是MAXN*logn,这里logn取20
void update(int p)
{
z[p].sum = z[z[p].l].sum + z[z[p].r].sum;
}
int build(int l, int r)
{
cnt++;
int p = cnt;
if(l == r)
{
z[p].sum = a[l];
return p;
}
int m = (l + r) >> 1;
z[p].l = build(l, m);
z[p].r = build(m + 1, r);
update(p);
return p;
}
int query(int l, int r, int rt, int nowl, int nowr)
{
if(nowl <= l && r <= nowr)
{
return z[rt].sum;
}
int m = (l + r) >> 1;
if(nowl <= m)
{
if(m < nowr)
{
return query(l, m, z[rt].l, nowl, nowr) + query(m+1, r, z[rt].r, nowl, nowr);
}
else
{
return query(l, m, z[rt].l, nowl, nowr);
}
}
else
{
return query(m+1, r, z[rt].r, nowl, nowr);
}
}
int modify(int l, int r, int rt, int p, int v)
{
cnt++;
int q = cnt;
z[q] = z[rt];
if(l == r)
{
z[q].sum += v;
return q;
}
int m = (l + r) >> 1;
if(p <= m)
{
z[q].l = modify(l, m, z[q].l, p, v);
}
else
{
z[q].r = modify(m+1, r, z[q].r, p, v);
}
update(q);
return q;
}
int n, m;
int main()
{
cin>>n;
for(int i = 1; i <= n; i++)
{
cin>>a[i];
}
cin>>m;
root[0] = build(1, n);
for(int i = 1; i <= m; i++)
{
int op;
cin>>op;
if(op == 1)
{
int p, v;
cin>>p>>v;
root[i] = modify(1, n, root[i-1], p, v);
}
else
{
int k, l, r;
cin>>k>>l>>r;
cout<<query(1, n, root[k], l, r)<<'\n';
root[i] = root[i-1];
}
}
return 0;
}
前缀值域可持久化线段树(主席树)
前缀和+可持久化线段树
点击查看代码
#include <iostream>
using std::cin;
using std::cout;
const int N = 2e5 + 10;
struct Node
{
int l, r; // 左儿子,右儿子
int sum; // 区间和
Node()
{
l = r = sum = 0;
}
} z[N * 30];
int n;
int cnt; // 节点数
int a[N];
int root[N]; // 第 i 个前缀应的值域线段树的根
void update(int p)
{
z[p].sum = z[z[p].l].sum + z[z[p].r].sum;
}
int build(int l, int r) // 返回这段区间对应的节点编号
{
cnt++;
int p = cnt;
if (l == r)
{
z[p].sum = a[l];
return p;
}
int m = (l + r) >> 1;
z[p].l = build(l, m);
z[p].r = build(m + 1, r);
update(p);
return p;
}
int query(int p1, int p2, int l, int r, int k)
// 当前对应的值域范围 l ~ r
// 要询问第 k 小的数
// 需要 p1, p2 两棵线段树来询问
{
if (l == r)
return l;
int m = (l + r) >> 1;
if (z[z[p2].l].sum - z[z[p1].l].sum >= k)
return query(z[p1].l, z[p2].l, l, m, k);
else
return query(z[p1].r, z[p2].r, m + 1, r, k - (z[z[p2].l].sum - z[z[p1].l].sum));
}
int modify(int l, int r, int rt, int p, int v)
{
cnt++;
int q = cnt; // 新的节点 q 用于修改
z[q] = z[rt];
if (l == r)
{
z[q].sum += v;
return q;
}
int m = (l + r) >> 1;
if (p <= m)
z[q].l = modify(l, m, z[q].l, p, v);
else
z[q].r = modify(m + 1, r, z[q].r, p, v);
update(q);
return q;
}
int main()
{
cin >> n;
int MAXV = 0;
for (int i = 1; i <= n; ++i)
cin >> a[i], MAXV = std::max(MAXV, a[i]);
int m;
cin >> m;
root[0] = 0;
for (int i = 1; i <= n; ++i)
root[i] = modify(1, MAXV, root[i - 1], a[i], 1);
// 主席树就建好了
for (int i = 1; i <= m; ++i)
{
int l, r, k;
cin >> l >> r >> k;
cout << query(root[l - 1], root[r], 1, MAXV, k);
}
return 0;
}
小技巧
1.换行
使用"\n"换行比endl快
#include<bits/stdc++.h>
using namespace std;
int main()
{
freopen("1.txt","w",stdout);//重定向到文件输出
for (int i=1;i<=10000000;i++)
//cout << i << endl;//14.08s
cout << i << "\n";//0.9579s
return 0;
}
2.双指针-区间计算
3.取模
众所周知,取模是一种速度很慢的运算,所以我们要考虑
在不影响答案正确性的前提下,尽可能少的进行取模运算
code
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int mo = 1000000007;
inline void inc(int &a,int b)
{
a+=b;if (a>=mo) a-=mo;
}
#define inc(a,b) {a+=b;if (a>=mo) a-=mo;}
int main()
{
res.sum = (1ll * res.sum * mul + 1ll * add * res.size) % mo;
//a = b+c*d;
a = (b + 1ll * c * d) % mo;
//a = b*c*d + e*f + g;
a = (1ll * b * c % mo * d + 1ll * e * f + g) % mo;
//a = a + b;
a += b; if (a >= mo) a-=mo;
//a = b*c-d*e
a = ((1ll * b * c - 1ll * d * e) % mo + mo) % mo;
//a = a - b
a -= b; if (a<0) a += mo;
return 0;
}




 浙公网安备 33010602011771号
浙公网安备 33010602011771号