点分治学习

例题：考虑一颗边权为1的树上有多少个路径正好为k的点对。

 

 

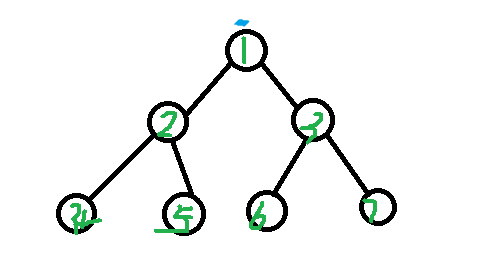
 我们考虑一个这样的树，现在问，这个树上有多少个点对之间的距离为k。

首先，我们从根结点开始考虑。

那么我们可以把所有的路径划分为两个部分

1，经过根结点的路径。2，不经过根结点的路径。

对于第一种路径，经过根节点，那么就是x->root->y。

也就是说这条路径是root的两个不同子树的链组成。

那么不就是考虑d[x] + d[y] == k的点对吗。

我们可以求的root到每个结点的距离，存放到d数组里面。

同时，保存每个结点是root的哪个子树下面的点 用b数组保存，保存root能到那些结点，用point数组保存。

那么我们可以把point数组根据距离进行排序。

从而用两个指针的方式将其进行统计。

对于第二种路径来说，

不就是递归第一种路径嘛。

例题链接：https://www.luogu.com.cn/problem/CF161D

#include"stdio.h"
#include"string.h"
#include"algorithm"
using namespace std;
inline int read(){
    int x=0,f=1;
    char c=getchar();
    while(c<'0'||c>'9'){
        if(c=='-')f=-1;
        c=getchar();
    }
    while(c>='0'&&c<='9'){
        x=(x<<3)+(x<<1)+c-'0';
        c=getchar();
    }
    return x*f;
}

const int N = 100010;

int head[N],ver[N],Next[N],edge[N],tot;
int n,m;
int v[N],Size[N],ans,root;///找到树的重心
int vis[N];
int d[N],b[N],point[N],top;
int cnt[N];
int num,k;

void add(int x,int y,int w){
    ver[++ tot] = y; edge[tot] = w;
    Next[tot] = head[x]; head[x] = tot;
}

void get_root(int x,int far,int n){///求子树的重心
   Size[x] = 1;
   int max_part = 0;
   for(int i = head[x]; i; i = Next[i]){
       int y = ver[i];
       if(vis[y] || y == far) continue;
       get_root(y,x,n);
       Size[x] += Size[y];
       max_part = max(max_part,Size[y]);
   }
   max_part = max(max_part,n - Size[x]);
   if(max_part < ans || root == 0) {
     ans = max_part;
     root = x;
   }
   return ;
}

void get_dist(int x,int far,int ww,int from){
    point[++ top] = x; b[x] = from;d[x] = ww;
    cnt[from] ++;
    for(int i = head[x]; i; i = Next[i]){
        int y = ver[i];
        if(y == far || vis[y]) continue;
    //    d[y] = d[far] + edge[i];
        get_dist(y,x,ww + edge[i],from);
    }
}
int cmp(int x,int y){
    if(d[x] == d[y]) return b[x] < b[y];
    return d[x] < d[y];
}
void calc(int root)
{
    top = 0;
    point[++ top] = root;
    d[root] = 0; b[root] = root;
    cnt[root] = 1;
    for(int i = head[root]; i; i = Next[i])
    {
        int y = ver[i];
        if(vis[y]) continue;
        cnt[y] = 0;
      //  d[y] = edge[i];
        get_dist(y,root,edge[i],y);
    }
    sort(point + 1,point + top + 1,cmp);
    int left = 1,right = top;
    while(left < right){
            if(d[point[left]] + d[point[right]] < k) left ++;
            else if(d[point[left]] + d[point[right]] > k) right --;
            else  {
                int xx = 0;
                int r = right;
                while(r > left){
                    if(d[point[r]] + d[point[left]] == k)
                        {
                            if(b[point[r]] != b[point[left]])
                                xx ++;
                        }
                    else break;
                    r --;
                }
                num += xx;
                left ++;
            }
        }
}

void solve(int u)
{
    vis[u] = 1; top = 0;
    calc(u);
    for(int i = head[u]; i; i = Next[i]){
        int y = ver[i];
        if(vis[y]) continue;
        ans = n; root = 0;
        get_root(y,0,Size[y]);
        solve(root);
    }
}
int main()
{
    n = read();k = read();
    for(int i = 1; i <= n - 1; i ++){
        int x,y,w;
        x = read(); y = read();w = 1;
        add(x,y,w); add(y,x,w);
    }

    ans = n;
    get_root(1,0,n);
    solve(root);

    printf("%d\n",num);
}