推荐系统

此系列笔记来源于

Coursera上吴恩达老师的机器学习课程

---

推荐系统

基于内容的推荐算法

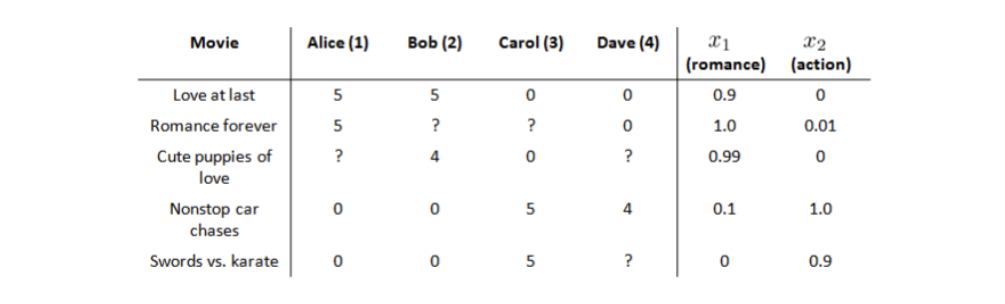
上图是一个 四位用户 对 五部电影的打分情况 加上 各电影的特征值

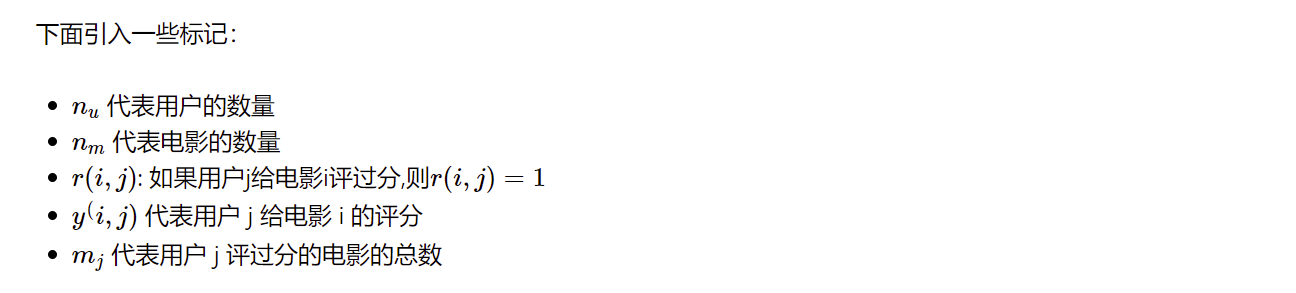
对于每个电影的特征值 $x^{(i)}$我们还要加上特征的截距项 $x^{(i)}_0$

如 $x^{(1)}=\begin{bmatrix} 1 \\ 0.9 \\0 \end{bmatrix}$

接下来要用线性回归模型来构建一个推荐系统算法，我们对每个用户都训练一个线性回归模型。

其中 $i:r(i,j)$ 表示我们只计算那些用户 j 评过分的电影。在一般的线性回归模型中，误差项和正则项应该都是乘以 $\frac{1}{2m}$，在这里我们将 m 去掉，因为这并不影响我们最小化代价函数。并且我们不对方差项$\theta_0$进行正则化处理。

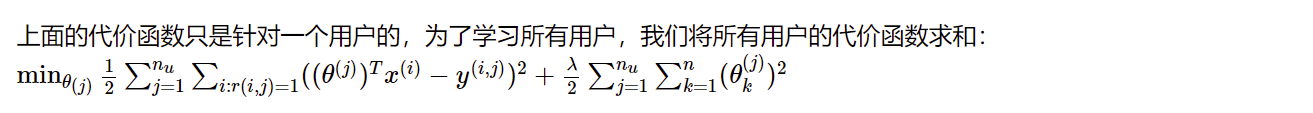
如果用梯度下降法求解，更新公式为：（偏导数部分已计算）

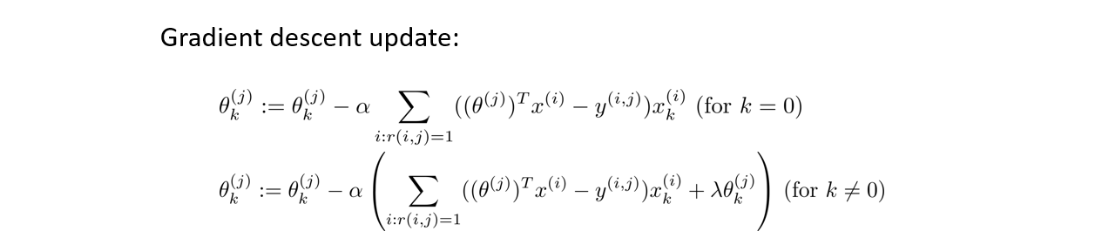
协同过滤

之前我们是根据可用的特征，训练出了每位用户的参数，但相反地，如果我们拥有用户的参数，我们也可以来学习得出电影的特征。

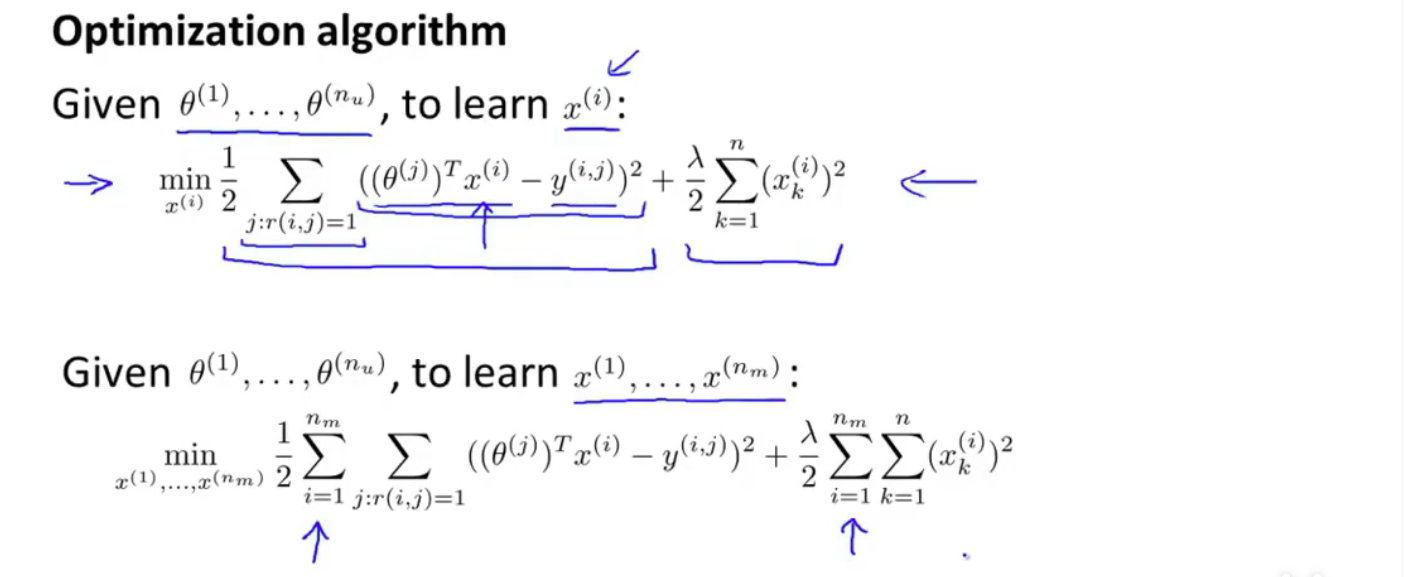
在这里，协同过滤算法便指的是 我们可以根据不同用户的评分，及参数，来学习电影的特征值，进而我们又可以用这些特征值去更好地预测用户的评分，就这样来不断的优化算法。

然而借由 $x$ 预测 $\theta$，再借由 $\theta$ 预测 $x$…… 这一过程我们可以高效地用一个式子来进行：

步骤：

1、初始化 $x^{(1)},\cdots,x^{(n_m)},\theta^{(1)},\cdots,\theta^{(n_m)}$为一些随机的小值

2、使用梯度下降算法最小化代价函数

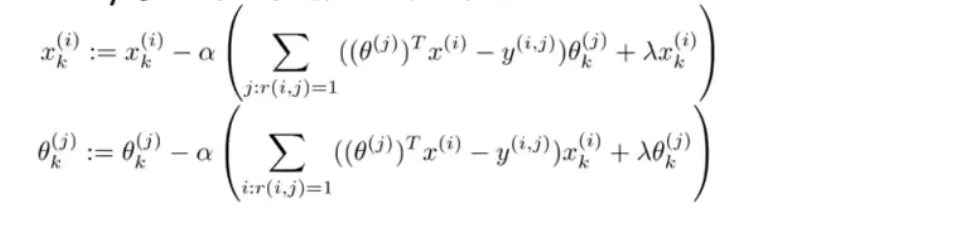
3、训练完算法后，我们便可以预测$(\theta^{(j)})^Tx^{(i)}$为用户 j 给电影 i 的评分

向量化

我们先将 所有用户对所有电影的评分 放在一个矩阵中

记作 $Y,\;Y(i,j)$表示第j名用户对第i部电影的评分

例：

我们的预测值：

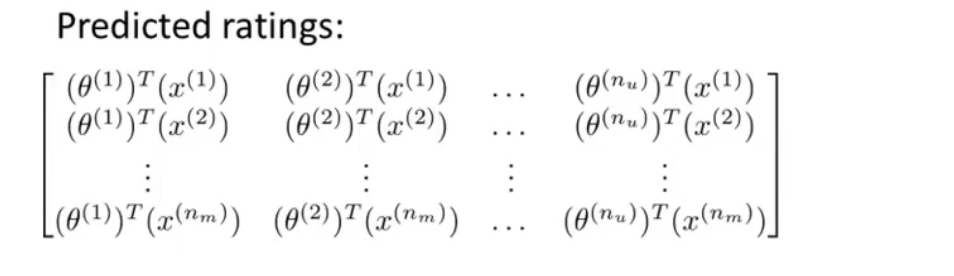
我们可以将电影的特征和用户的参数转化为一个大矩阵

这被称为低秩矩阵分解，接着计算这个预测评分的矩阵 $X\Theta^T$

另外在这里将不再需要 $x_0$ 和 $\theta_0$

寻找相关内容

对于电影 i 有特征 $x^{(i)}$，电影 j 有特征 $x^{(j)}$

当电影 i 和 电影 j 相关时，只需要 $||x^{(i)}-x^{(j)}||$ 较小即可

找到与电影 i 最相关的五部电影，就是找到$||x^{(i)}-x^{(j)}||$ 最小的五部电影 j

均值归一化

还是刚才的例子，此时我们增加一名新的用户 Eve，她从未对电影评过分

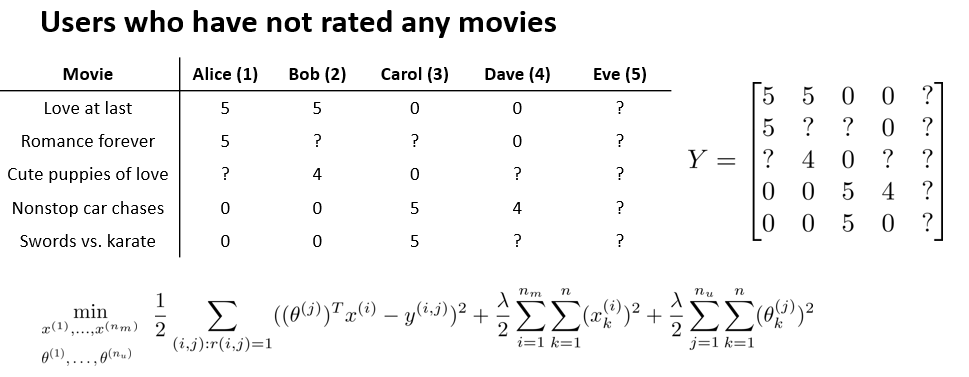
如果我们按照之前的步骤，那么我们最后计算出来 Eve的参数矩阵一定是零矩阵，那我们以什么为依据为 Eve 推荐电影呢？

这里我们就要用到均值归一化。

我们先对已知的其他用户对各个电影的评分求一个平均值，再将这些评分减去各个电影对应的均值

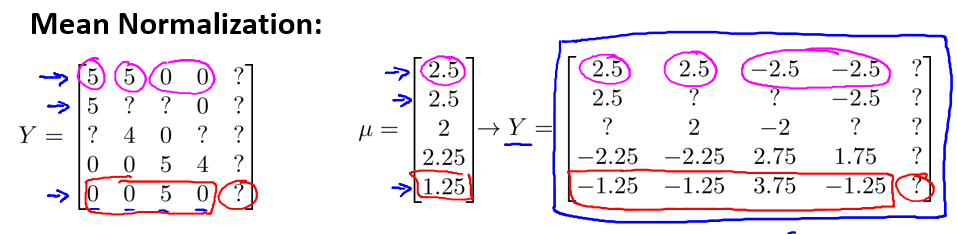
$\mu$ 就是均值矩阵

接着我们对这个新得到的 Y 矩阵来训练算法，步骤和之前一样。

如果我们要用这个新训练出来的算法预测评分，我们只需要预测的评分加上均值即可，即 $(\theta^{(j)})^Tx^{(i)}+\mu_i$，对于 Eve，新模型便会认为她给每部电影的评分都是平均分