误差分析

此系列笔记来源于

Coursera上吴恩达老师的机器学习课程

---

误差分析

评估一个学习算法

步骤：

1、首先我们先将数据集分为两部分 训练集 和 测试集 ，一般按 7 : 3 的比例

2、用训练集去学习 \(\Theta\) 并且 最小化 \(J_{train}(\Theta)\)

3、计算测试集的 测试误差 error \(J_{test}(\Theta)\)

测试误差的计算：

1、对于线性回归

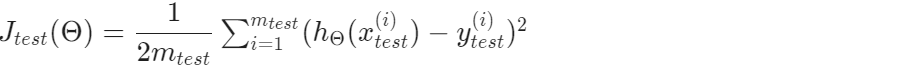
2、对于逻辑回归

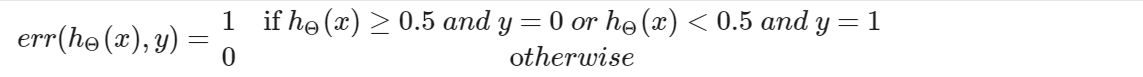
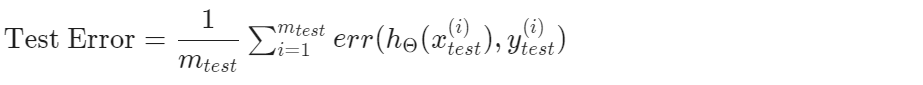
这将能告诉我们测试集数据被错误分类的比例

模型选择

当我们的假设函数与训练集非常拟合时，不能代表这个假设函数就是优秀的，可能会产生过度拟合，即对于新样本的表现并不如意。因此，我· 们需要选择更合适的假设函数模型。

步骤：

1、我们根据多项式次数分成好几个模型

2、将数据集分成三部分，一般来说为 训练集60%、验证集(Cross validation cv)20%、测试集20%

3、计算各模型的误差值

（1）用训练集来优化 \(\Theta\)参数

（2）用验证集来找出误差最小的多项式次数的模型

（3）用测试集来估计泛化误差值‘

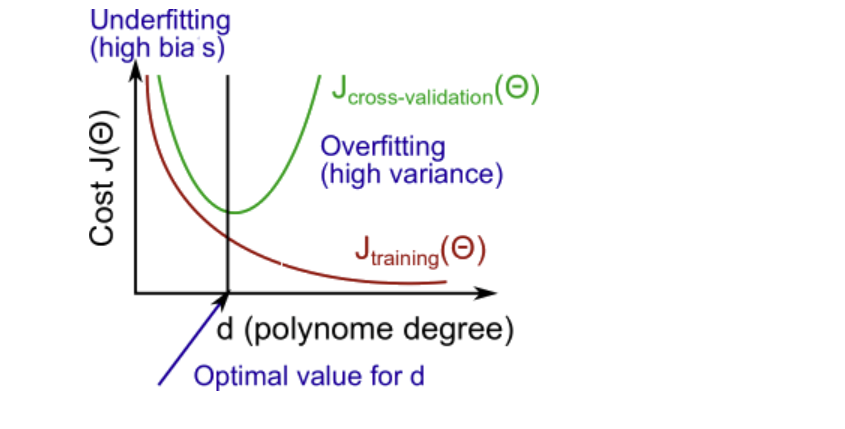
高偏差 bias 和 高误差 variance

高偏差对应着欠拟合underfitting，高误差对应着过度拟合overfitting

高误差时，\(J_{train}(\Theta)\) 和 \(J_{CV}(\Theta)\) 都很高，且 \(J_{train}(\Theta) \approx J_{CV}(\Theta)\)

高偏差时，\(J_{train}(\Theta)\) 很小， \(J_{CV}(\Theta)\) 远高于 \(J_{train}(\Theta)\)

正则化 与 偏差和误差

对于正则化的参数 \(\lambda\) 我们也要进行选择，如果太小，会出现过度拟合，太大则会出现欠拟合。

步骤：

1、建立一个 \(\lambda\)列表，一般依次为两倍关系，(i.e. λ∈{0,0.01,0.02,0.04,0.08,0.16,0.32,0.64,1.28,2.56,5.12,10.24})

2、建立一个不同degrees的模型集合 或者是其他不同变量

3、遍历每个\(\lambda\)，对于每个\(\lambda\)遍历所有模型来学习 \(\Theta\)

4、用学习到的 \(\Theta\) 计算\(error_{CV}\)（不使用正则化）

5、选择在 Cross Validation set 上产生最低误差的最佳组合

6、使用最佳组合的 \(\Theta\) 和 \(\lambda\) 应用于测试集，看看其效果

学习曲线

高偏差：high bias

样本量少时：

\(J_{train}(\Theta)\)很小， \(J_{CV}(\Theta)\)很大

样本量多时：

\(J_{train}(\Theta)\) 和 \(J_{CV}(\Theta)\)都很大，且两者值逐渐靠近

高误差：high variance

样本量少时：

\(J_{train}(\Theta)\)很小， \(J_{CV}(\Theta)\)很大

样本量多时：

\(J_{train}(\Theta)\) 逐渐增加，\(J_{CV}(\Theta)\)逐渐减小，且不趋于平稳状态。\(J_{train}(\Theta)<J_{CV}(\Theta)\)，但两者差距始终很大

![image-20220513204626698](https://img2022.cnblogs.com/blog/1754203/202205/1754203-20220513204626958-1354891981.png)

在此之后我们应该做的：

对于神经网络来说，隐藏层、参数越少，往往更容易欠拟合，但是更好计算。相反，隐藏层、参数越多，往往更容易过渡拟合，此时我们可以采用正则化来解决这一问题，但是这将增大电脑的计算量

低阶多项式一般会 high bias 和 low variance，往往模型的拟合程度不是很好

高阶多项式一般会 low bias 和 high variance，模型对训练集的拟合程度非常好，但新样本则并不。

一般我们希望选择一个介于两者之间的模型。

对偏斜类的误差度量

简单解释下偏斜类，举个例子，判断病人是否得了癌症，数据集中为1的占比量非常大，或者为0的占比量非常大，这样的数据倾斜会导致我们算法训练出来的效果偏差十分巨大。

对此我们提出精准率Precision 和 召回率Recall 来对偏斜类进行误差度量

预测类 \ 实际类	1	0
1	True positive	False positive
0	Fake negative	Fake negative

我们定义 \(Precision=\frac{True\;positive}{True\;pos\;+\;Fake\;pos}\)

即 预测是阳性的数据中真实为阳性的比例

定义 \(Recall=\frac{True\;positive}{True\;pos\;+\;Fake\;neg}\)

即 真实为阳性的数据中被预测到的比例

精准率和召回率之间的权衡

在上面用癌症作为例子的逻辑回归中，我们最初定义

\(0\le h_{\theta}(x)\le1\)，如果 \(h_{\theta}(x) \ge 0.5\)，预测 1；如果 \(h_{\theta}(x)<0.5\)，预测 0

当我们增大 0.5 时， 我们会得到一个高精准率，低回归率结果

反之减小 0.5 时，我们会得到一个低精准率，高回归率的结果

我们令这个 0.5 变为 临界值threshold

我们通过改变临界值，来获得一个不同P值和R值的结果

那么精准率和召回率应该如何权衡呢？

我们可以通过调和平均数来计算\(F\)值，以此来评判这个算法，在这里越高越好

\(F:2\frac{PR}{P+R}\)

另外，当我们有一个低偏差，高方差（多参数）的训练模型（如神经网络）时，有一个庞大的训练集（包含足够多的特征）往往能帮我们训练出高性能的模型。