线性回归和逻辑回归

一、线性回归
线性回归对多维空间中存在的样本点，用特征的线性组合去拟合多维空间中点的分布和轨迹。线性回归的公式如下：

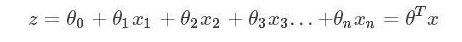
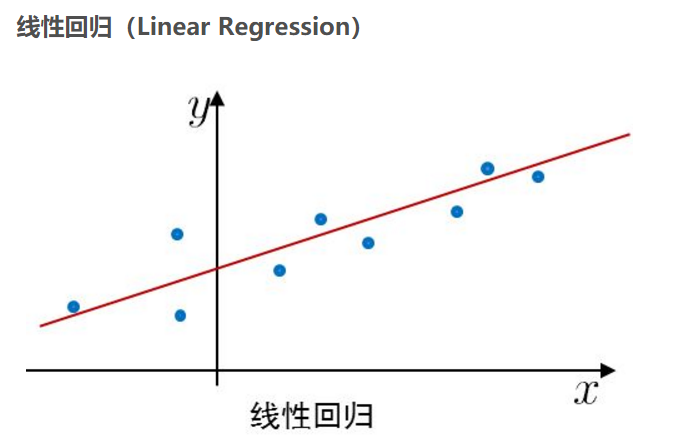
（数学名称的简单理解体会：坐标系里的点回归到一条直线上，离散的数据点拟合成一条连续的直线）
二、逻辑回归
通常是利用已知的特征变量来预测一个离散型目标变量的值(如0/1，是/否，真/假)。通过拟合一个逻辑函数来预测一个事件发生的概率，预测值是一个概率值(0-100%),根据概率值的大小,映射为目标变量的分类值,如:概率值大于等于 50%,映射目标变量分类值为 1,概率值小于 50%,映射目标变量分类值为 0。
对于逻辑回归来说，其思想也是基于线性回归。逻辑回归中选择对数几率函数（logistic function）作为激活函数，对数几率函数是Sigmoid函数（形状为S的函数）的重要代表

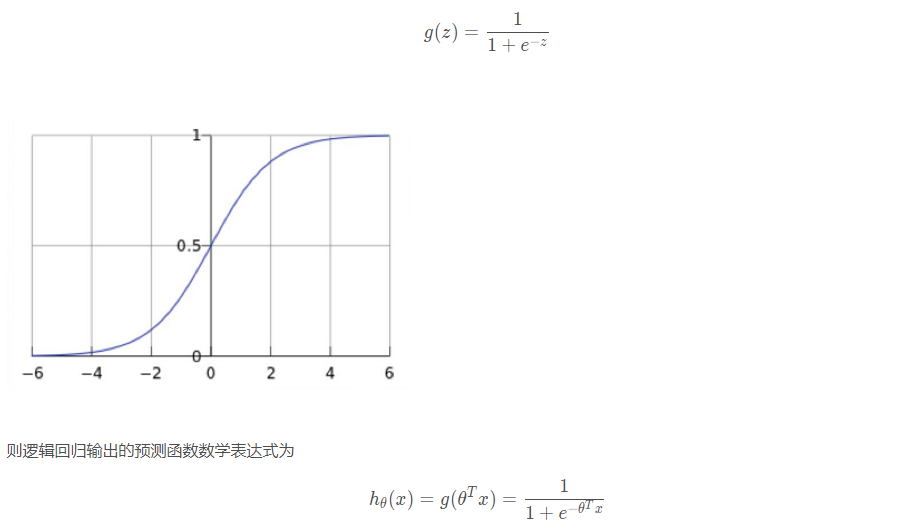
逻辑回归算法将线性函数的结果映射到了sigmoid函数中。
（数学名称的简单理解体会：逻辑回归，逻辑即数学常说的0/1,是/否,真/假。回归即归为某一类）