一些题目

感觉咕了好久了。

\({\Large 约定}\)：

1. 用集合符号表示位运算符号，用 $ \oplus $ 表示异或，特别的，$ i \in S$ 表示二进制数 \(S\) 的第 \(i\) 位为 \(1\)
2. 用 \(V\) 表示值域，\(\sum\) 表示字符集，\(\omega\) 表示 bitset 的常数 \((\omega = 64)\)
3. 除去用 \(()/[]\) 表示开闭区间外，\([]\) 仅表示艾弗森约定，\(\{\}\) 仅表示集合,括号嵌套全用 \(()\)
4. 字符串或序列角标为区间表示对应区间的子串

CF1553E Permutation Shift

1900 tag 暴力 构造 数学 图论

感觉对题目观察得比较细致就太不难了。显然对于一个 \(k\) 我们可以做到在 \(\mathcal{O}(n)\) 的复杂度内完成判断，具体实现可以看 CF1768D，但肯定不能对所有 \(k\) 全都做一遍。但你看数据范围的时候你会发现 \(m\leq \frac{n}{3}\)。如果说 \(m\) 对题目无关显然可以取到 \(n\)，说明这个 \(m\) 对我们比较重要。
一次操作最多让两个数回到自己的位置上，\(m\) 次操作最多让 \(2m\) 个数回到自己的位置上，说明另外的 \(n-2m\) 个数就要在正确的位置。因为 \(m\leq \frac{n}{3}\)，所以 \(n-2m\geq \frac{n}{3}\)。因为一个数只会在其中一个 \(k\) 的时候回到自己的位置，那么满足条件的 \(k\) 显然不会超过 \(3\) 个，这样就可以完成这道题了。
但细节确实有点多。QAQ

submission

2025.12.05

CF1466F Euclid's nightmare

2100 tag 并查集 图论 贪心 数学

之前 vp 过一场 ABC，做过一道思路上比较像的题。同样是一个集合，两个集合之间能够到达当且仅当集合中至少有一个数相同。显然我们可以把一个集合看成一个虚点，给集合之间连边。但是直接连边显然是不太行的，所以我们需要让数字作为中转点再做 dfs。
再回到这道题上。显然我们可以沿用连边的这个技巧。假如说某一个向量中有两个坐标为 \(1\)，那么我们就可以把这两个坐标对应的点连起来。当选了这条边的时候这两个数被选的次数就要加 \(1\)，也就是这两个点的度数加 \(1\)。那么我们就可以把向量的选和不选转化成图上边的选和不选。
那如果向量只有一个坐标为 \(1\) 要怎么办？那就把它转化成两个坐标为 \(1\) 的情况！我们可以新建一个虚点，假设为 \(m+1\)。我们把向量为 \(1\) 的坐标对应的那个点和 \(m+1\) 连边。显然 \(m+1\) 的情况是由其他向量被动决定的，所以这么做是没有问题的。
当我们把每个向量都这么处理完后会形成若干个联通块。现在考虑其中的一个联通块。显然我们并不能直接处理这个联通块，因为可能会出现不同的选边导致相同的情况。那我们考虑什么时候会出现相同的情况。

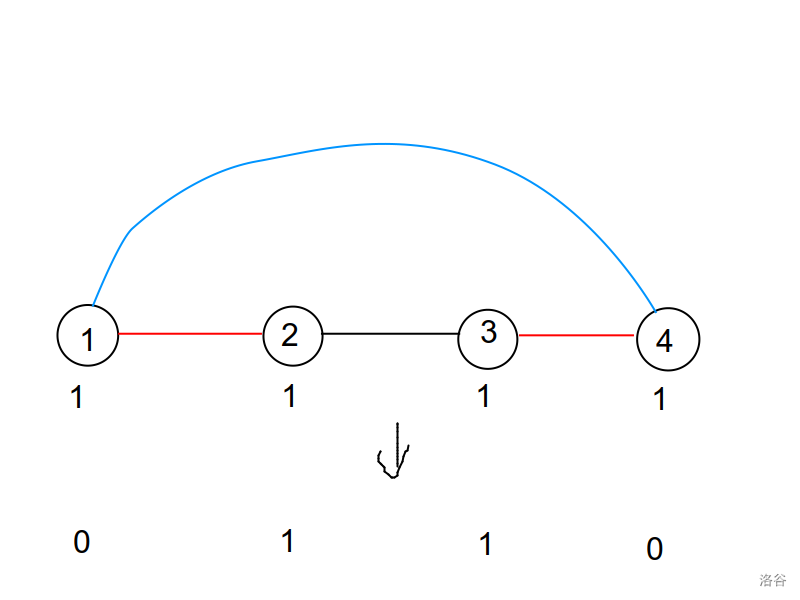
假如说红边为我们原本就选的边，黑边为不选的边，下面第一行数字为这个数被选的次数 \(\mod2\)。
现在我们要加入一条蓝边，那么这些数字出现的次数就变成第二行了。
但是我们可以找到另一种方法不用加这条边也可以达到同样的效果。

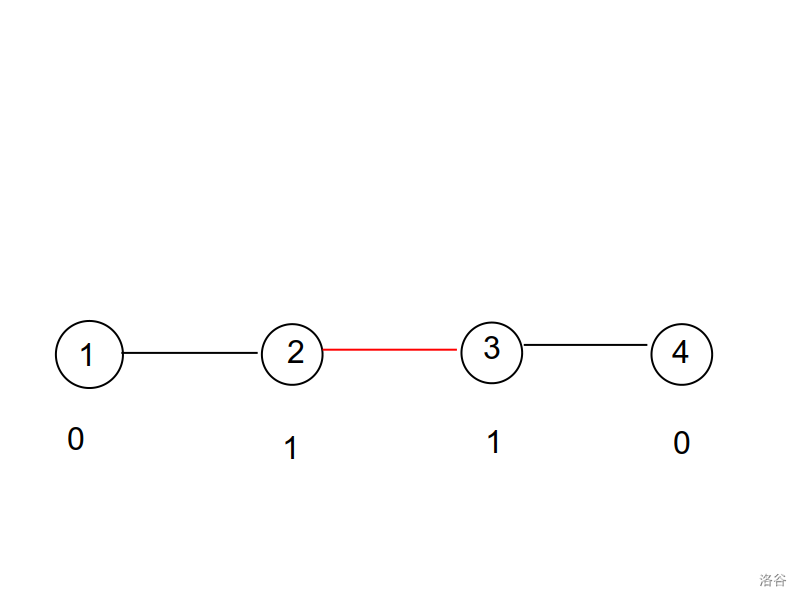
这说明假如你加入的这条边的两个点在同一个联通块内，那么这条边就可以不加。这个显然就是并查集了。假设这个并查集内有 \(sz_i\) 个点，那么就有 \(sz_i-1\) 调边。我们把一个联通块看成一棵树，那么从下往上，每一条边的选和不选都会导致最终每个点的状态不同，因此对于一个联通块总共有 \(2^{sz_i-1}\) 种不同的情况。假设有 \(cnt\) 个联通块，那么总共有 \(\prod_{i=1}^{cnt}2^{sz_i-1}=2^{\sum_{i=1}^{cnt}sz_i-1}\)。那哪些向量是我们要选的呢？显然我们在加边的时候就可以确定这些向量了。

submission

2025.12.05

CF1322B Present

2100 tag 构造 贪心 数学 双指针

感觉很有意思的一道题。之前做这种有关和的异或的题很多都不会做，这道题给了一点启发。
看到异或想到按位考虑，假设当前处理到第 \(k\) 位，设 \(b_i\) 表示第 \(i\) 个数在二进制下的后 \(k\) 位。考虑两个数的和什么时候这位会为 \(1\)，显然两种情况：

1. 不进位，\(b_i+b_j\in [2^i,2^{i+1}-1]\)
2. 进位，\(b_i+b_j\in [3\times 2^i,2\times (2^{i+1}-1)]\)
   然后就可以将 \(b_i\) 排序，再用双指针统计一下数量就行了。

submission

2025.12.05

CF1406D Three Sequences

2200 tag 构造 贪心 数学

怎么我这都不会了QAQ
首先考虑没有修改时的情况，假如一开始 \(a_i\) 都相同，那么可以把所有 \(b_i\) 都等于 \(a_i\)，所有 \(c_i\) 都为 \(0\)。
\(b\) 中的最大值为 \(b_n\)，\(c\) 中的最大值为 \(c_1\)，\(\max(b_i,c_i)=\lceil \frac{b_n+c_1}{2} \rceil\)
考虑 \(a\) 的差分数组 \(d\)。我们只需要考虑修改对 \(b_n\) 的影响，显然 \(b_n=\sum_{i=1}^{n}[d_i \geq 0]\times d_i\)，\(c_1\) 只要在修改的时候修改就行了。

submission

2025.12.05

CF1327D Infinite Path

2200 tag 图论 数学 枚举 贪心

感觉这种题好多都是变成置换环的啊。
唉唉一开始题目理解错了所以不明白为啥保证答案一定存在了。

我们还可以定义排列 \(a\) 和 \(b\) 的乘积为排列 \(c = a \times b\)，其中 \(c[i] = b[a[i]]\)。此外，排列 \(p\) 的 \(k\) 次幂定义为 \(p^k = \underbrace{p \times p \times \dots \times p}_{k \text{ 次}}\)。

这是题目中对两个排列乘积的定义。看到无限序列的定义：\(i, p[i], p[p[i]], p[p[p[i]]], \dots\)，其中所有元素的颜色都相同（即 \(c[i] = c[p[i]] = c[p[p[i]]] = \dots\)）。可以发现每次向后跳动就想到置换环（显然这很置换环）。假设目前我们的排列 \(p\) 变成了排列 \(d\)，那么 \(d'=d\times p\)，\(d'_i=p_{d_i}\)，也就是说，\(d'\) 每一位上的值是 \(d\) 每一位上的值在置换环 \(p\) 上向后移一位，\(p^k\) 就是向后移动 \(k-1\) 位。注意到如果你的置换环的长度跟你的操作次数之间没有整除关系的话，那么环长是不会变的。所以我们只要枚举环长的因数然后暴力做一遍就好了，取最小的那个就行。

submission

2025.12.11

CF1498E Two Houses

2200 tag 图论 交互 数学 贪心

有一点巧妙的题目，感觉要会一点性质才行。
题解咋都有 \(\mathcal{O}(n)+{\text 不询问}\) 的爆标做法啊。/jk
性质可以去看常用trick的 性质1，这里也放一下。
考虑拓扑序最小的几个强连通分量的并集 \(S\)，\(S\) 内的点全部向 \(S\) 外的点连边，所以 \(S\) 内所有点的入度和等于 \(\binom {|S|}2\)，反之亦然。

引理：在竞赛图中，如果 \(u\) 能到达 \(v\) 而 \(v\) 不能到达 \(u\)，即 \(u\) 的拓扑序严格小于 \(v\)，那么 \(k_u < k_v\)

证明：如果 \(v\) 不能到达 \(u\)，\(\exists S,u \in S \land \forall x \in S, y \not \in S,x \rightarrow y\)，即集合 \(S\) 内的点全部向 \(S\) 外的点连边。

\(\therefore k_v \ge |S|,k_u < |S| \Rightarrow k_u < k_v\)

发现如果想两两到达必须在同一个强联通块内，根据上面的性质可以发现拓扑序最小的几个强联通分量的并集中包含的点的度数也一定是最小的。那么可以按照入度排序之后看看这些数的和是否到达 \(\binom {|S|}2\) 就好了。如果到达了说明新加入了一个强联通块。

submission

2025.12.11

CF1408D Searchlights

2000 tag 动态规划 模拟 暴力枚举

小清新题。
有下面三种操作方式：

1. 一直向上走，直到纵坐标比所有探照灯的纵坐标都大
2. 一直向右走，直到横坐标比所有探照灯的横坐标都大
3. 向上走一段路后，再向右走一会儿
   我们开一个数组 \(f_{x}\) 表示所有的海盗先统一向上走了 \(x\) 步后，最少需要向右走几步。最后的答案就是 \(\max \{ i+f_{i} \}\)。
   那么就两两枚举 \(i\) 和 \(j\)，用两者 \(y\) 和 \(x\) 的差去更新一下 \(f_i\) 就好了。
   最后求答案的时候倒着枚举就可以考虑到那些还没有离开范围的位置的答案了。因为去除无用的灯可以发现灯的横坐标递增，纵坐标递减，那么这是正确的。

submission

2025.12.11

CF1438C Engineer Artem

2000 tag 数学 枚举

感觉想到了按照黑白染色的奇偶方式去构造就很容易了，因为奇偶性不同说明一定不相同。
感觉其他类似的题目也要往这方面想想。

submission

2025.12.11

CF741C Arpa’s overnight party and Mehrdad’s silent entering

2600 tag 图论 构造 DFS

感觉很巧妙的题目喵，我怎么想不到喵QAQ。
看这个题目就很像二分图，因为一条边的两个端点的颜色显然是不同的。但是还有相邻 \(3\) 个点不能同色的限制，显然我们要构造出一种方法使得按照这张图染色得到的结果一定是符合条件的。显然3个数中至少有一对相邻的点颜色是不同的。那么我们就可以把其中一些相邻的点连边作为限制。我们发现可以把 \(2i-1\) 和 \(2i\) 连边，这样就可以满足题目的限制并且是一张二分图。
我们将 \(2i-1\) 和 \(2i\) 的连边染成黑色，将题目给出的两点的连边染成白色，可以发现一个点只会连一条白边和一条黑边，也就是说，一条路径一定是黑白黑白这样循环下去的，并且最后一个一定和开头不一样，那么说明这里面没有奇环，一定是一张二分图。
那好像输出 -1 就是骗人的？

submission

2025.12.24