结对项目(python)———自动生成小学四则运算题目的命令行程序
- 项目
| 软件工程 | 班级 |
|---|---|
| 作业要求 | 作业要求 |
| 作业目标 | 完成小学四则运算题目的命令行程序,熟悉项目开发流程,提高团队合作能力 |
| 作者信息 | 吴茗睿 -- 3118005385、杨锐楷 -- 3118005389 |
| Github地址 | Github地址 |
项目要求
实现一个自动生成小学四则运算题目的命令行程序(也可以用图像界面,具有相似功能)。
- 使用 -n 参数控制生成题目的个数,例如
Myapp.exe -n 10
将生成10个题目。
- 使用 -r 参数控制题目中数值(自然数、真分数和真分数分母)的范围,例如
Myapp.exe -r 10
将生成10以内(不包括10)的四则运算题目。该参数可以设置为1或其他自然数。该参数必须给定,否则程序报错并给出帮助信息。
- 生成的题目中计算过程不能产生负数,也就是说算术表达式中如果存在形如e1− e2的子表达式,那么e1≥ e2。
- 生成的题目中如果存在形如e1÷ e2的子表达式,那么其结果应是真分数。
- 每道题目中出现的运算符个数不超过3个。
- 程序一次运行生成的题目不能重复,即任何两道题目不能通过有限次交换+和×左右的算术表达式变换为同一道题目。例如,23 + 45 = 和45 + 23 = 是重复的题目,6 × 8 = 和8 × 6 = 也是重复的题目。3+(2+1)和1+2+3这两个题目是重复的,由于+是左结合的,1+2+3等价于(1+2)+3,也就是3+(1+2),也就是3+(2+1)。但是1+2+3和3+2+1是不重复的两道题,因为1+2+3等价于(1+2)+3,而3+2+1等价于(3+2)+1,它们之间不能通过有限次交换变成同一个题目。
生成的题目存入执行程序的当前目录下的Exercises.txt文件,格式如下:
- 四则运算题目1
- 四则运算题目2
……
其中真分数在输入输出时采用如下格式,真分数五分之三表示为3/5,真分数二又八分之三表示为2’3/8。
- 在生成题目的同时,计算出所有题目的答案,并存入执行程序的当前目录下的Answers.txt文件,格式如下:
- 答案1
- 答案2
特别的,真分数的运算如下例所示:1/6 + 1/8 = 7/24。
- 程序应能支持一万道题目的生成。
- 程序支持对给定的题目文件和答案文件,判定答案中的对错并进行数量统计,输入参数如下:
Myapp.exe -e
.txt -a .txt 统计结果输出到文件Grade.txt,格式如下:
Correct: 5 (1, 3, 5, 7, 9)
Wrong: 5 (2, 4, 6, 8, 10)
需求分析(python)
-
生成表达式:随机生成运算数、运算符,式子长度即运算符个数随机。
生成运算数:random.randrange() ;
生成运算符:先定义一个运算符列表,每次随机从中选取一个;
随机式子长度:for循环中随机选取2-4以内的循环量,每循环一次选取一个运算数(生成1个符号的式子,需要2个数,生成3个运算符的式子需要4个数)
-
获取答案及对比:利用python的eval函数可直接获取字符串的运算值;
转化真分数:如67/8写为8'3/8,先将真分数转为整数int_t,原数t减去整数int_t得到差los_t,最后int_t 、"'"符号、los_t组成结果
-
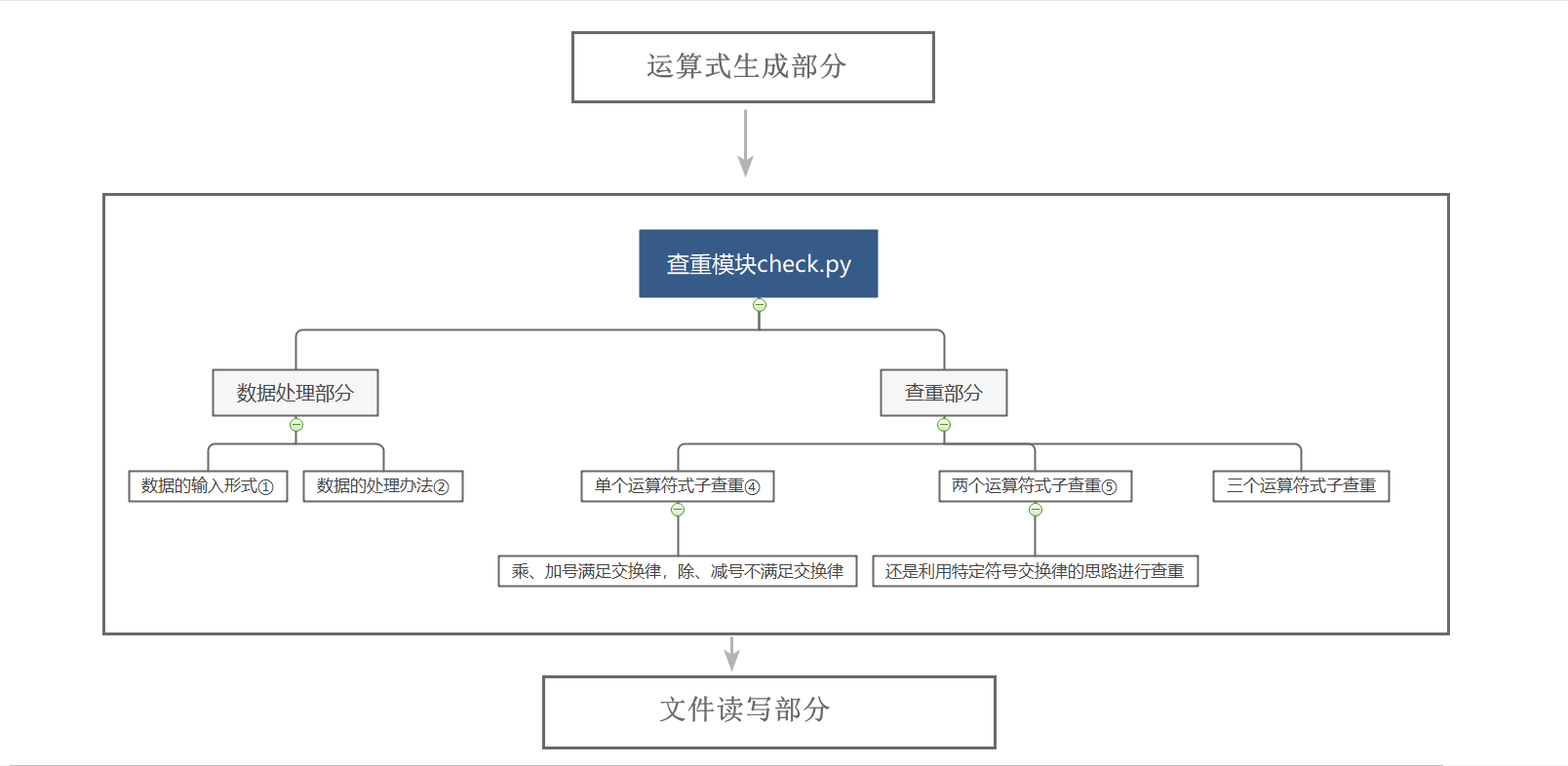
查重模块:
&ensp由于在网上查找了很多资料都没有发现相关范例或已证明有效的算法实例,因此只能自己动手,设计一套三脚猫算法出来。
以下思路参考即可,
各位看官大佬轻喷
①数据的输入形式:
由于题目要求运算式中带有分数、带分数这些玩意儿,因此,在输入的时候,式子同以下格式:
exp = '1 + 2 * 3'
exp = "1'1/2 + 2 ÷ 3"
可以看到,运算数和运算符号之间,是间隔有一个空格的;并且,使用“/”来表示分数,使用“÷”来表示除法运算(如果用“/”表示除法运算的话处理起来那真是太乱了)。
注释:
运算数和运算符之间使用空格来分隔,有利于对整条运算式作.split()分割,也有利于使用正则去提取运算符,方便后期处理。②:数据的处理办法
由于运算式由以上的方式输入进来,因此,我们再使用算术的方法来确定式子是否重复就显得较为麻烦。因此,我们打算采用字符串比较的方法,
来确定两条式子是否重复。因此,当式子进入到方法里边之后,首先调用.split()方法提取所有的运算数和运算符,记为exp_list。然后再使用正则表达式,
仅提取两式子的运算符(通过比较两式子使用的运算符种类是否相同,达到一个初步的筛选过滤效果),记为op_list。然后,我们对输入进来的表达式做一次算术运算,
得到表达式的结果,记为result。特别地,对于exp_list中可能出现的带分数字符串,我们要用“+”号替换“'”号,方便进行运算。在后边,我们将会建立一个字典,字典的键
就是各个式子的result值,而键值就是运算结果相同的式子所组成的一个列表。这样来处理数据让我们能够在尽可能小的范围内查重,不至于让其他纷繁复杂的式子变换扰乱思绪。③:查重部分的设计理念:
首先我们要明白为什么式子会重复。在题目要求上说,“即任何两道题目不能通过有限次交换+和×左右的算术表达式变换为同一道题目”。我们知道,乘法和加法是满足交换律的,
因此后面我们基于交换律来设计一个查重算法。④:单运算符的查重:
对于单运算符的两条式子,当两条式子运算符均为“*”或“+”的时候,直接取运算符两侧的运算数(其实是字符串),来进行对比,看是否是从一个式子交换而来即可。
当两条式子运算符为“-”或“÷”的时候,由于这两者不满足交换律,因此肯定不重复(前提:两运算式字符串不能相同)。⑤:双运算符的查重:
对于两个运算符的式子,设计查重算法之前应当自己拿纸笔看下这两种符号排列组合出来的运算式,怎样才算重复的,怎样才算不重复,最后得到一个概括性的结论出来之后,
设计算法就相对没那么难了。例如,当两条运算式中运算符号有且只有乘号的时候,两条式子中运算数无论怎么变换顺序都是重复的;然后是“*”、“+”号组合,
查重的时候必须要先拿出乘号两边的运算数,跟上面一样,判断是否能够交换顺序得到另一条式子,从而判断式子是否重复。
由于缺乏数学论证,具体比较的式子就不放出来了,上面只提供一个可能的设计思路。 -
命令行参数输入实现程序运行:使用正则表达式
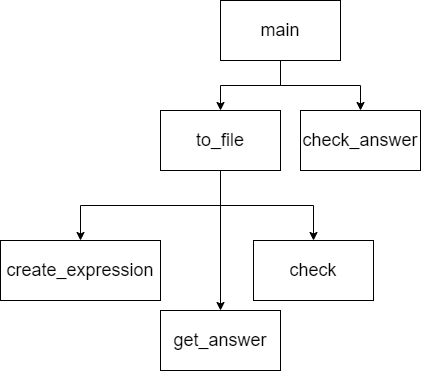
函数说明(只贴出重要函数代码)
-
create_expression(erange=10)erange参数:为生成数的大小范围;
功能:随机生成算数式子,长度,数字(整数、分数)随机
def create_expression(erange=10): operator = [' + ', ' - ', ' * ', ' / '] # 符号 end_operator = ' =' equation = '' # 初始式子,为空 bag = [] # 为随机数的空列表,随机从里面取字 nature_step = random.randrange(1, 3) # 随机数的间隔 # print(nature_step) for i in range(5): bag.append(str(random.randrange(1, erange, nature_step))) for i in range(5): denominator = random.randrange(1, 10) # 分母 molecule = random.randrange(1, 10) # 分子 denominator, molecule = max(denominator, molecule), min(denominator, molecule) # 比较大小同时交换 fraction_number = molecule / denominator fraction_number = Fraction('{}'.format(fraction_number)).limit_denominator() # 小数转换为真分数 bag.append(str(fraction_number)) for i in range(4): denominator2 = random.randrange(1, 10) # 分母 molecule2 = random.randrange(1, 10) # 分子 denominator2, molecule2 = max(denominator2, molecule2), min(denominator2, molecule2) # 比较大小同时交换 fraction_number2 = denominator2 / molecule2#对调分子分母位置以生成带分数 fraction_number2 = Fraction('{}'.format(fraction_number2)).limit_denominator() # 小数转换为真分数 int_t = int(fraction_number2) los_t = fraction_number2 - int_t if (int_t != 0 and los_t != 0): fi_t = str(str(int_t) + "'" + str(los_t)) else: fi_t = str(fraction_number2) bag.append(fi_t) len_bag_randint = random.randrange(2, 4) # print(len_bag_randint) for i in range(len_bag_randint): # 随机取bag里的数 randint_number = random.randint(0, len(bag) - 1) equation += bag[randint_number] if i < len_bag_randint - 1: equation += operator[randint_number % len(operator)] # else: # equation += end_operator bag.pop(randint_number) return equation -
get_answer(question)question参数:算数式子
功能:利用python的eval函数获取算数式子的答案,具有将假分数转为真分数的功能
-
to_file(need=10, erange=10)need、 erange参数:need生成式子的数量,erange数字的范围
功能:生成式子并合法的式子写入Exercises.txt,答案写入Answers.txt
-
check_answer(e_fliepath, a_filepath)e_fliepath, a_filepath参数:e_fliepath是存储式子的文件,a_filepath是存放答案的文件
功能:检查e_fliepath文件里面的答案是否正确,并输出正确答案式子的下标correct :() ,错误答案式子的下标wrong = :()到Grade.txt
-
check
功能:式子查重
import re
import copy
class check:
def __init__(self):
self.dic = {}
'''
__check私有方法:
功能:
用来进行运算式查重.每传入一个运算式,都会将其记录到字典中,并依据该字典来进行查重。
传入参数:
'''
def check(self, expression): #传入的expression如:“9 * 1/9 * 1”,又如:“1'8/9 + 2 +3 ”
c_exp = re.sub("'","+",expression) #将运算式中的点替换成加,用来运算算式结果。
c_exp = re.sub("÷",'/',c_exp)
result = eval(c_exp)
if result<0:
return 0
try: # 在字典中能够找到相同的键,即进入查重步骤
if self.dic[result]: # result所对应的键值是一个列表,列表成员为一个个表达式。相同结果的不同表达式将会被存放在该列表当中
list_len = len(self.dic[result])
j=0
while j<list_len: #exp是列表中的算式,expression是外部传入的算式
exp_exist = self.dic[result][j]
op_list1 = re.findall(r'[\+\-\*÷]', exp_exist) # 找到运算式中的运算符
op_list2 = re.findall(r'[\+\-\*÷]', expression)
exp_orig = exp_exist.split() # 包含运算数、运算符的列表
exp_out = expression.split()
if len(op_list1) == len(op_list2) == 1: # 当两条式子都只有一个运算符的情况下
if op_list1 == op_list2: # 运算符相同的情况下
if '+' in op_list2:
if (exp_orig[0] == exp_out[2]) and (exp_orig[2] == exp_out[0]):
return 0
else:
j+=1
continue
elif '*' in op_list2:# 如['2','*','3']与['3','*','2'],[1 * 6] [2 * 3]
if (exp_orig[0] == exp_out[2]) and (exp_orig[2] == exp_out[0]):
return 0
else:
j+=1
continue
else: # 两个运算符相同,但是不是加号或乘号,只需要比较两式中第一个数即可。
if exp_orig[0] == exp_out[0]: # 当被除数\被减数相同,二运算式运算结果也相同,那么这两条式子必定重复。
return 0
else:
j+=1
continue
else: # 运算符不相同,结果相同,因此式子一定不重复。
j+=1
continue
elif len(op_list1) == len(op_list2) == 2: # 当两条式子都含有两个运算符的情况下,先判断两个运算符是否一样。使用到队列。
op_queue = op_list1
for op in op_list2: # 通过这种办法能够看两个运算式是否包含了相同的运算符号。
try:
op_queue.remove(op)
except:
pass
if len(op_queue) == 0: # 两运算式的运算种类符号相同
try:
c_exp_out = exp_out
for i in range(len(exp_orig)):#看两个列表能不能相互抵消,如果能,说明两个运算式运算符、运算数都是一样的
c_exp_out.remove(exp_orig[i])
#当两条列表能够抵消完,判断符号类型。
op_tuple = set(op_list2) #去重。
if len(op_tuple) == 1:#“++”或“**”类型
if '+' in op_tuple: #++的类型,
return 0
elif '*' in op_tuple:# **
return 0
else:#"÷÷ 的类型"
j+=1
continue
elif len(op_tuple) ==2:
if expression == self.dic[result][j]:
return 0
elif ('+'in op_tuple) and ('*' in op_tuple):#{'+','*'}
orig_index = exp_orig.index('*')#exp = '1 * 2 + 3'
#exp = '2 * 1 + 3'
out_index = exp_out.index('*')
if (exp_out[out_index+1] == exp_orig[orig_index-1]) and(exp_out[out_index-1] == exp_orig[orig_index+1]):
return 0
j+=1
continue
else:
j+=1
continue
except: # 如果remove出错,说明两条式子有运算数不同,说明不等效
j+=1
continue
else: # 两运算式的运算符号不同,但是结果相同,说明两式子是不重复的
j+=1
continue
else:
j+=1
continue
self.dic[result].append(expression)
return 1
except: # 在字典中找不到相同的键,将该运算式加入到该字典当中。
if result<0:
return 0
self.dic[result] = []
self.dic[result].append(expression)
return 1
main()
功能:完成命令行参数控制生成式子数量以及数字范围、对比答案的功能;
调用了以上5个函数。
def main():
t1 = time.time()
str_input = ''
for w in range(1,len(sys.argv)):
str_input +=sys.argv[w]
#-n10000-r10
try:
need_mode = '-n([\d]+)'
erange_mode = '-r([\d]+)'
need = int(re.search(need_mode,str_input).group(1))
erange = int(re.search(erange_mode,str_input).group(1))
if (need <=0) or (erange<=0):
print('[-]参数值范围指定有误')
print('[-]exiting')
return
else:
to_file(need = need,erange= erange)
t2 = time.time()
print('Execute time:%.2f' %(t2-t1))
return 0
except:
try:
e_file_mode = r'-e((.*?).txt)'
e_file = re.search(e_file_mode,str_input).group(2)+'.txt'
a_file_mode = r'-a((.*?).txt)'
a_file = re.search(a_file_mode, str_input).group(2)+'.txt'
if os.path.exists(e_file) and os.path.exists(a_file):
check_answer(e_fliepath=e_file, a_filepath=a_file)
t2 = time.time()
print('Execute time:%.2f' % (t2 - t1))
return 0
else:
print('[-]输入的文件路径有误')
print('[-]exiting')
return
except:
print("[-]文件扩展名有误或路径有误!")
print('[-]exiting')
return
测试
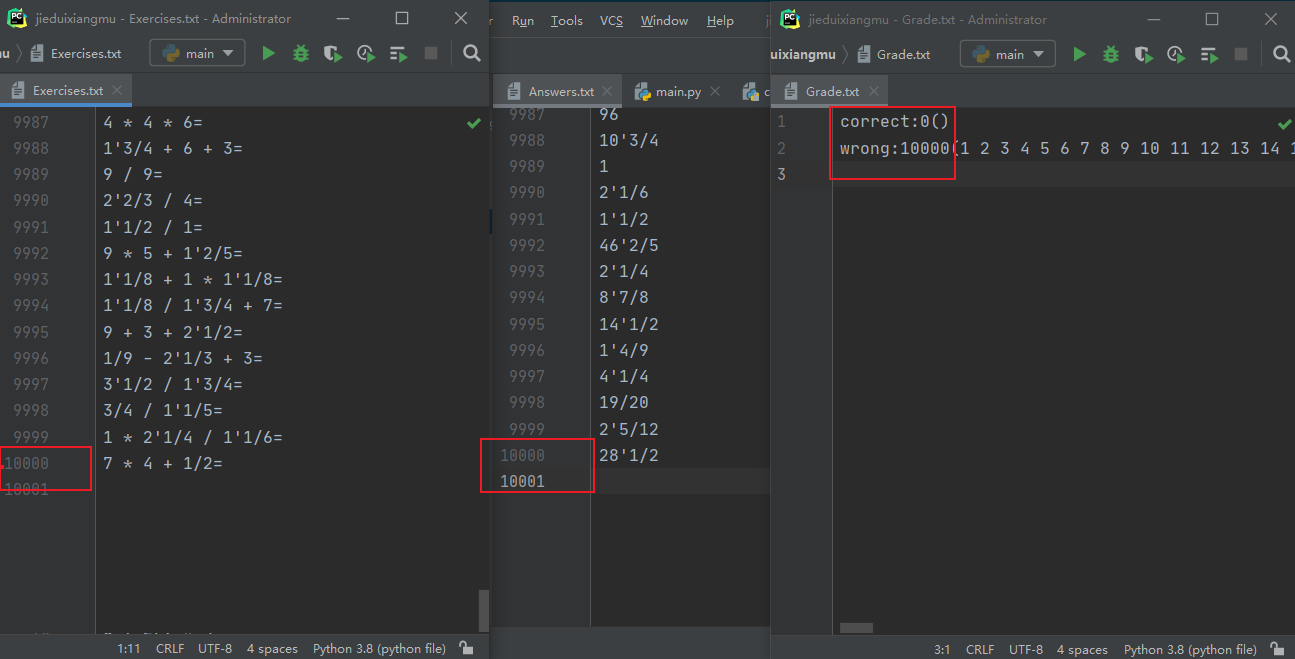
- 生成10道题目

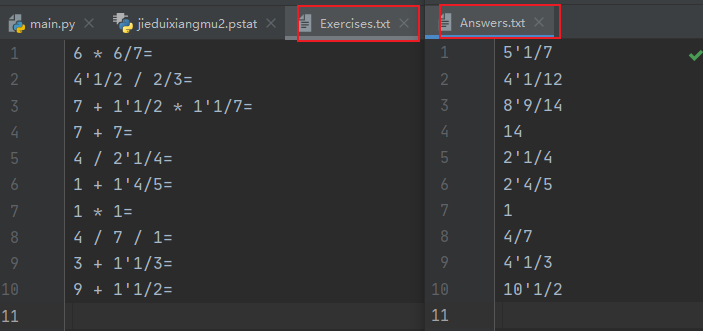
答案判断:(题目1,2,7输入了正确答案)

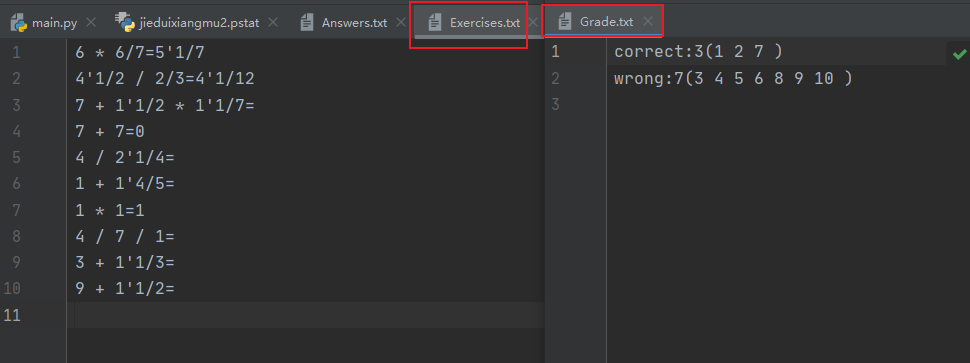
-
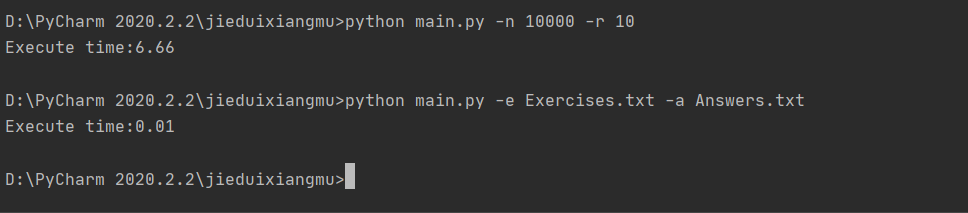
生成10000道题目
(时间有点长,[改进check查重模块]改进前时间是11秒左右,改进后为6.66秒)
![]()
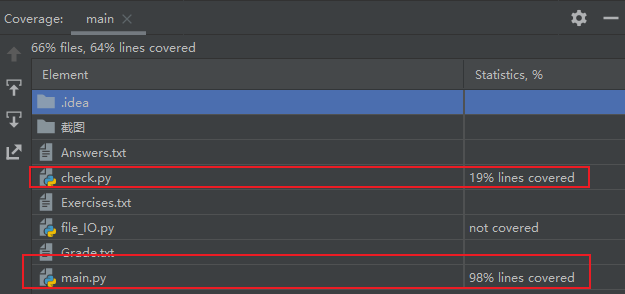
代码覆盖率
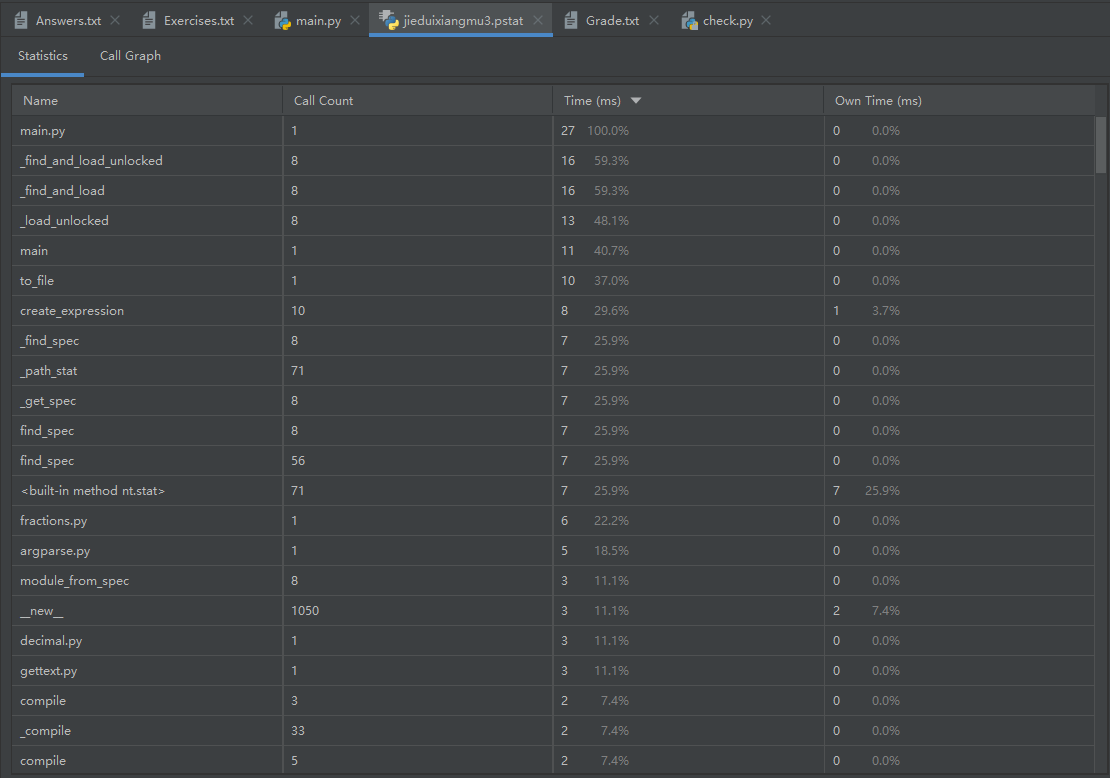
各模块效能
项目总结
吴茗睿:
对于一个团队协作的项目,应当先设计一套主体框架出来,然后再再主体框架上进行某些重要功能的设计。脱离了主体框架,或是在主体框架出来之前就设计模块功能,很多时候是浪费时间的。譬如此次项目中,我在式子生成程序还没做好之前就把查重模块给弄了,结果生成式子模块一调用,好家伙,那些运算数、分数、带分数问题在原先的查重模块上是没法解决的,只能够重新设计。
同时,进行团队的项目,应当要在事先了解好模块和模块对接的细节。在此项目来说,就应该在事先了解生成的式子是什么情况的,运算数的表示形式如何等等。
最后,就是自己写的模块应当具备良好的注释,注释应当包括:模块的功能、模块的输入参数是什么,模块的返回值是什么,什么条件下会产生这个返回值。并且这种注释习惯应当从始至终,即便模块经过非常大规格上的重写、迭代,也要相应地更改注释。以方便别人能够理解代码内容。
杨锐楷:
完成这个结对项目后,自己对团队合作更加了解。在队友吴大佬的带领下,学到蛮多新的知识。完成项目的时候吴大佬负责最难的check查重模块和命令行参数输入,我负责生成较简单的生成表达式、获取答案、对比答案、文件写入。
项目期间,遇到挺多意外的。由于吴佬先写了check模块,导致后面程序基本成型的时候,在生成1万道题目是,数量达不到,只有4000左右。后来分析得出,是check和生成式子模块的问题和没有添加括号,在create_expression函数增加类似2‘1/2形式的真分数,式子数量增加到7000左右,再次修改check模块后,式子能够生成10000道式子。
团队合作要注意代码规范,给予适当的注释,让成员知道如何使用,如何运作,用意是什么。合作前要商量主要模块的具体形式,以免最后整合是出错,导致大量修改。
PSP表格
| PSP2.1 | Personal Software Process Stages | 预估耗时(分钟) | 实际耗时(分钟) |
|---|---|---|---|
| Planning | 计划 | 20 | 20 |
| · Estimate | · 估计这个任务需要多少时间 | 10 | 10 |
| Development | 开发 | 540 | 580 |
| · Analysis | · 需求分析 (包括学习新技术) | 20 | 20 |
| · Design Spec | · 生成设计文档 | 10 | 10 |
| · Design Review | · 设计复审 (和同事审核设计文档) | 20 | 20 |
| · Coding Standard | · 代码规范 (为目前的开发制定合适的规范) | 10 | 10 |
| · Design | · 具体设计 | 240 | 280 |
| · Coding | · 具体编码 | 300 | 320 |
| · Code Review | · 代码复审 | 40 | 40 |
| · Test | · 测试(自我测试,修改代码,提交修改) | 200 | 250 |
| Reporting | 报告 | 30 | 30 |
| · Test Report | · 测试报告 | 30 | 30 |
| · Size Measurement | · 计算工作量 | 15 | 15 |
| · Postmortem & Process Improvement Plan | · 事后总结, 并提出过程改进计划 | 15 | 15 |
| 合计 | 950 | 1160 |



 浙公网安备 33010602011771号
浙公网安备 33010602011771号