【LeetCode】98.验证二叉搜索树

【LeetCode】98.验证二叉搜索树

/*	
*  转载请说明出处与作者
*  作者：多巴胺dopamine
*/

一 问题描述

1 题目

​ 给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

​ 有效二叉搜索树定义如下：

​ 节点的左子树只包含 小于 当前节点的数。

​ 节点的右子树只包含 大于 当前节点的数。

​ 所有左子树和右子树自身必须也是二叉搜索树。

示例 1：

**输入：**root = [2,1,3] **输出：**true

示例 2：

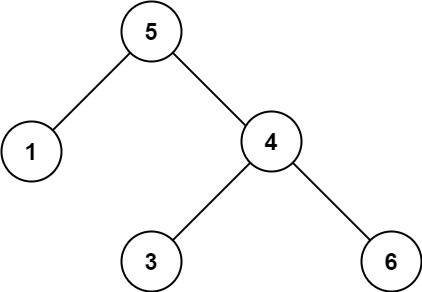
**输入：**root = [5,1,4,null,null,3,6] 
**输出：**false 
**解释：**根节点的值是 5 ，但是右子节点的值是 4 

提示：

​ 树中节点数目范围在[1, 104] 内

​ -231 <= Node.val <= 231 - 1

2 一些些知识点

2.1 二叉搜索树的一个性质

​ 二叉树的搜索树的中序遍历为一个递增序列。

2.2 前驱节点

​ 当前节点前访问的那个节点。

二 解题

1 解题思路

1.1 第一种方法

​ 中序遍历，形成一个中序遍历序列。检查概中序遍历数组是否递增。

1.2第二种方法

​ 同样是中序遍历，但是一边遍历一边判断。

​ 中序遍历时，只要当前每个节点都大于其前驱节点，该二叉树就一定会是一个标准的二叉搜索树。

​ 以示例2说明：

​ 其中序遍历的顺序为：1 -> 5 -> 3 -> 4 -> 6。

​ 在访问4时，其前驱节点时3；在访问6时，其前驱节点是4。

2 代码

2.1 第一种方法

/**
* Definition for a binary tree node.
* struct TreeNode {
*     int val;
*     struct TreeNode *left;
*     struct TreeNode *right;
* };
*/
void inorder_traversal();
bool judge_order();
# define max_size 10000
/*
* 初始化函数
*/
bool isValidBST(struct TreeNode* root){
  //	开辟中序遍历数组空间
  int* numbers=(int *)malloc(sizeof(int)*max_size);
  //	开辟中序遍历数组当前指针的空间以及初始化
  int* point=(int *)malloc(sizeof(int));
  *point=0;
  //	中序遍历
  inorder_traversal(root,numbers,point);
  //	判断，is使用int类型没有问题，在 C 语言中 bool 实际以 int 大小存储。0为 false ,1为 true
  int is=judge_order(numbers,point);
  return is;
}
/*
* 中序遍历函数
* 参数说明：
* root,当前节点；numbers,中序遍历的数组；point,中序遍历数组当前指针。
*/
void inorder_traversal(struct TreeNode* root,int* numbers,int* point){
  //递归的临界条件
  if(root){
    inorder_traversal(root->left,numbers,point);
    //将当前节点的值添加到中序遍历的数组
    numbers[*point]=root->val;
    (*point)++;
    inorder_traversal(root->right,numbers,point);
  }
}
/*
* 中序遍历遍历数组检查函数（检查是否是递增）
* 参数说明：
* numbers,中序遍历的数组；point,中序遍历数组的大小。
*/
bool judge_order(int* numbers,int* point){
  bool is=true;
  int i=0;
  for(i=0; i<(*point)-1; i++){
    if(numbers[i] >= numbers[i+1]){
      is=false;
      break;
    }
  }
  return is;
}

2.1 第二种方法

相比较第一种方法，该方法不需要开辟一个中序遍历数组的空间同时也不用遍历之后在检测数组是否递增。

/**
* Definition for a binary tree node.
* struct TreeNode {
*     int val;
*     struct TreeNode *left;
*     struct TreeNode *right;
* };
*/
//使用 typedef 将结构重新命一下名
typedef struct TreeNode TreeNode;
//	前驱节点的指针
struct TreeNode* pre;
//	返回判断结果
bool is_true;
void inoreder_traversal();
/*
*	初始化函数
*/
bool isValidBST(struct TreeNode* root){
	pre=NULL;
	is_true=true;
	inoreder_traversal(root);
	return is_true;
}
/*
*	中序遍历函数
*/
void inoreder_traversal(TreeNode* root){
	//	递归的临界条件
	if(root){
		inoreder_traversal(root->left);
		//	如果前驱节点不是NULL，且前驱节点的 val 值大于当前节点的 val 值，那么这个二叉树不是二叉搜索树。
		//	至于为什么要求 pre 不为 NULL,可以自己想 
		if(pre && root->val <= pre->val){
			is_true=false;
		}
		//	左子树遍历结束，设置当前节点为前驱节点。
		pre=root;
		inoreder_traversal(root->right);
	}
}

三 总结

二叉树的题目多数都是其不同遍历方式的改造。遇到二叉树的题目从递归，其几种遍历方式这几个点入手思考。