【leetcode】96.不同的二叉搜索树

【leetcode】96.不同的二叉搜索树

/转载请说明出处与作者/

/作者：多巴胺dopamine/

一 问题描述

1 题目

​ 给你一个整数 n ，求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种？返回满足题意的二叉搜索树的种数。

​ 题目链接： 96. 不同的二叉搜索树 - 力扣（LeetCode）

​ 示例 1：

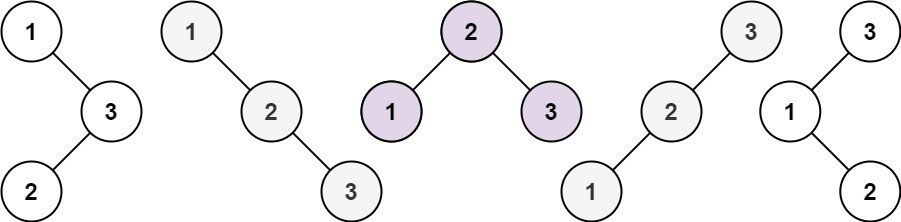
输入：n = 3
输出：5

示例 2：

输入：n = 1
输出：1

提示：

• 1 <= n <= 19

2 一些些需要了解的概念

2.1 二叉搜索树（Binart Search Tree）

​ 二叉搜索树又叫二叉查找树、二叉排序树。

​ 二叉搜索树首先是二叉树，且具有以下性质：

​ （1）若左子树不空，则左子树所有节点的值均小于根节点的值。

​ （2）若右子树不空，则右子树所有节点的值均大于根节点的值。

2.1.1 特点和应用

​ 可以实现快速的插入和删除，同时查找也具有一定优势。

​ 主要在文件系统和数据库系统采用这种数据结构进行排序和检索。

2.2 动态规划

​ 动态规划和递归有一定关系。

​ 核心思想：拆解问题，记住过往，减少重复计算。

二 解题

1 解题思路

​ （1）遇到树相关的问题很快就想到了递归的方法（树的遍历可以用递归来解决）。

​ （**2）仔细研究会发现如下规律： **

​ 规定N（0）= 1，这是根据后面发现的规律进行的规定。实际意义：空的二叉排序树也是一种情况。

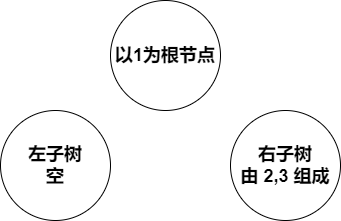
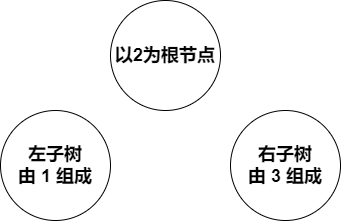
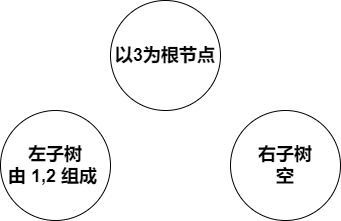
​ 注：以 n=3 为例讲解一下规律是怎么发现的（抱着找递归的思维去找，即分解问题）

图（1）	图（2）	图（3）

​ 会发现当以 1 为根节点时，左子树为空，右子树为一个二叉排序树（且n=2）。依次类推，得到上面的公式。

​ （3）提交代码发现超时，思考如何解决超时问题。

​ （4）首先想到的就是以空间换时间，也就变成了动态规划问题。

​ 本题的递归与动态规划之间有一定联系，见最后的总结部分。

2 代码

2.1 递归代码（超时，作为借鉴）

//二叉搜索树的性质：左子树小于根节点，右字数大于根节点
/*
* 参数说明：
* n,n个节点的二叉搜索树
*/
int numTrees(int n){
  //返回变量
  int retu_number=0;
  //边界条件
  if(n==1||n==0){
    retu_number=1;
  }else{
    // 每次循环是：以 i 为根节点的二叉搜索树的个数
    // left：以 i 为根节点，其左子树节点的个数
    // right：以 i 为根节点，其右子树节点的个数
    int i;
    for(i=1; i<=n ;i++){
      int left=i-1;
      int right=n-i;
      retu_number=retu_number+numTrees(left)*numTrees(right);
    }
  }
  return retu_number;
}

2.2 动态规划_1

//二叉搜索树的性质：左子树小于根节点，右字数大于根节点
void countTress();
/*
* 初始化函数
* 参数说明：
* n,n个节点的二叉搜索树
*/
int numTrees(int n){
  //开辟记录N（n）值的数组的空间
  int* Tree_numbers=(int *)malloc(sizeof(int)*20);
  int i;
  //循环，先计算N（1），再计算N（2）,最后计算到N (n)。
  //countTress() 仅被调用 n+1 次
  for(i=0;i<=n;i++){
    countTress(i,Tree_numbers);
  }
  return Tree_numbers[n];
}
/*
* 计算n个节点的二叉搜索树的种数
* 参数说明：
* n,n个节点的二叉搜索树； Tree_numbers，记录N（n）值的数组
*/
void countTress(int n,int* Tree_numbers){
  Tree_numbers[n]=0;
  // 临界条件
  if(n==0||n==1){
    Tree_numbers[n]=1;
  }else{
    // 这里也用到了递归的思想，但是没有重复调用 countTress() 函数
    // 而是直接访问记录之前结果的数组
    int i;
    for(i=1; i<=n ;i++){
      int left=i-1;
      int right=n-i;
      Tree_numbers[n]=Tree_numbers[n]+Tree_numbers[left]*Tree_numbers[right];
    } 
  }
}

2.3 动态规划_2

与动态规划_1差别不大，只是将两个函数合并成为一个，作为一个参考（可能会减少一定运行时间，毕竟调用函数比较浪费时间）

int numTrees(int n){
  int* Tree_numbers=(int *)malloc(sizeof(int)*20);
  int i;
  for(i=0;i<=n;i++){
      Tree_numbers[i]=0;
  if(i==0||i==1){
    Tree_numbers[i]=1;
  }else{
    int j;
    for(j=1; j<=i ;j++){
      int left=j-1;
      int right=i-j;
      Tree_numbers[i]=Tree_numbers[i]+Tree_numbers[left]*Tree_numbers[right];
    } 
  }
  }
  return Tree_numbers[n];
}

三 总结

​ 本题的递归与动态规划是有一定联系，但不确定是否使用所有的动态规划问题，因为并未对所有动态规划问题进行总结。（可以作为一种思考思路）

1 动态规划与递归的总结

​ 如果使用递归的算法（以求 N（3）为例）：是先求 N（3），在计算 N（3）时发现需要 N（2），依次类推。

​ 会发现 N（2）计算了 2 次， N (1) 计算了 6次 ......，发现递归使得出现了很多的重复计算。

​ 那么可不可以换一种思路（以空间换时间）：

​ 当我要从 N（n）时，我先去求 N （0），将它记录下来，再去求 N（1），一直到 N（n）。

​ 当用到前面的值时，直接去查询记录的数组就可以了。这样就将该函数调用了减少到了 （n+1） 次，也就变成了动态规划问题。