树与二叉树第一次总结
树
一对多的数据结构
树相关概念:
树叶:没有儿子的节点;
兄弟:具有相同父亲的节点;类似还有祖父和孙子节点。
深度:某节点的深度为树根到该节点的唯一路径的长度。
层次:深度相同的节点在同一层中,深度值为层数。
树高度:叶节点的深度最大值。
二叉树:一种特殊的树,每个双亲的孩子数不超过2个(0个,1个或2个),提供对元素的高效访问。有左孩子和右孩子。
二叉树
是树的一种转换,也是一种特殊的树
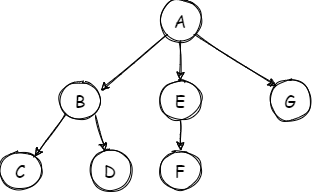
树-->二叉树
左儿子,有兄弟

将根节点A作为二叉树的根节点,然后将A节点的最左边的子节点B作为二叉树A的左子节点,由于根节点再无兄弟节点,此时以B为根节点来看,其最左边的子节点C作为其左子节点,其兄弟节点E作为其右子节点,然后将C作为根节点来看,其没有子节点,但有兄弟节点,则将其兄弟节点E作为右子节点,此时B附近的节点用尽,则以E为根节点,使其子节点F为左子节点,兄弟节点G为右子节点,此时树中无其他节点,二叉树建树完成.
二叉树的性质
- 在二叉树中的第i层上至多有$2^(i-1)$个结点(i>=1)。
- 深度为k的二叉树至多有$2^k - 1$个节点(k>=1)。
- 对任何一棵二叉树T,如果其叶结点数目为$n_0$,度为2的节点数目为n2,则$n_0=n_2+1$。
- 满二叉树:深度为k且具有$2^k-1$个结点的二叉树。即满二叉树中的每一层上的结点数都是最大的结点数。
- 完全二叉树:深度为k具有n个结点的二叉树,当且仅当每一个结点与深度为k的满二叉树中的编号从1至n的结点一一对应。
- 具有n个节点的完全二叉树的深度为$log_2n + 1$。
二叉树的遍历
二叉树遍历其实有六种,由于常见的都是从左至右,所以忽略了右至左的三种
-
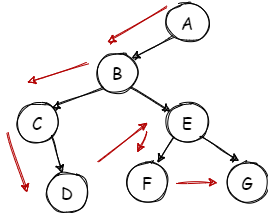
前序遍历:根左右
![Untitled Diagram (18).png]()
-
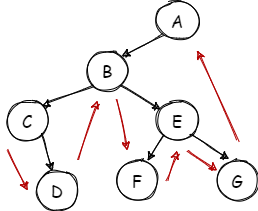
中序遍历:左根右
-
![Untitled Diagram (19).png]()
-
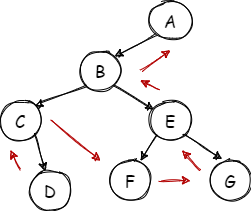
后序遍历:左右根
-
![Untitled Diagram (20).png]()
BST(Binary Search Tree)
二叉搜索树,左右子节点有大小之分,一般左子节点小于父节点,右子节点大于父节点
BST的代码实现
类的基础设置
class BSTree<T extends Comparable<T>>{
private Node root;//根节点
private int size;//树中存储数据的个数
//内部类
class Node {
T value;
Node left;//左子节点指向
Node right;//右子节点指向
public Node(T value, Node left, Node right) {
this.value = value;
this.left = left;
this.right = right;
}
}
}
- 由于BST的每个节点都有左子节点和右子节点,则在内部类中除了value参数以外,还要设定left和right的左右子节点指向
- 由于BST的左右子节点有大小之分,所以泛型需要继承Comparable接口,以方便后续例用compareTo来比较
- root根节点和size是为了后续在其他操作中使用
增加方法add
通过循环遍历增加
public boolean add(T value) {
//判断是否是null
if (value == null) throw new IllegalArgumentException("illegal value");
//判断是否为空,如果为空,则赋值给root,如果不为空,则分别向左右比较
Node node = root;
Node nodeF = null;//父节点
int judge = 0;
if (size == 0 || root == null) {
root = new Node(value, null, null);
size++;
return true;
} else {
//当循环到node为空时则无法再继续比较
while (node != null) {
judge = node.value.compareTo(value);//这一句与初始化分开的原因是防止空指针异常
//左小右大,当node大的时候,向左走
if (judge > 0) {
nodeF = node;
node = node.left;
} else if (judge < 0) {//右小左大,当node大的时候,向右走
nodeF = node;
node = node.right;
} else {
return false;
}
}
if (judge > 0) {
nodeF.left = new Node(value, null, null);
} else {
nodeF.right = new Node(value, null, null);
}
size++;
return true;
}
}
需要注意的点
- 需要判断是否是空链表
- 需要判断要增加的值是不是null
- nodeF的设置,为了最后增加节点时通过nodeF的left和right来进行插入,避免直接通过node赋值,导致插入的节点与原来的树没有关系
- node.value.compareTo(value)需要固定赋值给某个变量,以防止空指针异常
递归增加方法
public boolean addRecursion(T value) {
//判断是否是null
if (value == null) throw new IllegalArgumentException("illegal value");
int oldSize = size;
root = add1(root, value);
return oldSize < size;
}
public Node add1(Node node, T value) {
//递归出口
if (node == null) {
size++;
return new Node(value, null, null);
}
int judge = value.compareTo(node.value);
if (judge > 0) {
//向右遍历
node.right = add1(node.right, value);
} else if (judge < 0) {
//向左遍历
node.left = add1(node.left, value);
} else {
return root;
}
return node;
}
需要注意的点:
- 依旧需要判断是否为null
- 但是不用判断空链表问题
- 有两个方法, addRecursion为插入并且判断是否插入成功,插入成功通过判断oldSize是否小于size,add1为递归插入
查询方法
查询方法
public boolean isContain(T value) {
//判断是否是null
if (value == null) throw new IllegalArgumentException("illegal value");
Node node = root;
while (node != null) {
if (value.compareTo(node.value) > 0) {
node = node.left;
} else if (value.compareTo(node.value) < 0) {
node = node.right;
} else {
return true;
}
}
return false;
}
删除方法
常规删除方法
public boolean remove(T value) {
//判断是否是null
if (value == null) throw new IllegalArgumentException("illegal value");
Node node = root;
Node nodeF = null;
while (node != null) {
if (value.compareTo(node.value) > 0) {
nodeF = node;
node = node.right;
} else if (value.compareTo(node.value) < 0) {
nodeF = node;
node = node.left;
} else {
break;
}
}
//如果没找到,则删除失败
if (node == null) return false;
//如果是度为2的节点
if (node.left != null && node.right != null) {
Node minNode = node.right;
Node minNodeF = node;
while (minNode.left != null) {
minNodeF = minNode;
minNode = minNode.left;
}
node.value = minNode.value;
if (minNode.right != null) {
minNodeF.left = minNode.right;
} else {
minNodeF.left = null;
}
size--;
return true;
}
//如果是度为1的节点或者叶子节点
//这里两种情况放在一起看了,因为不管是要删除的节点是nodeF的right还是left,给其赋值时,都都是node.left或者node.right,如果是单边节点,则刚好赋值,如果是叶子节点,这两个点刚好是null,因此可以一举两得
if (nodeF.left == node) {
nodeF.left = node.left != null ? node.left : node.right;
} else {
nodeF.right = node.left != null ? node.left : node.right;
}
size--;
return true;
}
需要注意的点:
- 需要判断是否为空链表
- 需要对度为2的节点,以及叶子节点和单边节点进行分类讨论
- 删除度为2的节点时,一般采用找到以此节点为根的左子树中最大的点,或者右子树中最小的节点来替换这个节点,然后删除替换的点
- 删除叶子节点和单边节点可以放在一起看,详情看代码注释
递归删除方法
public boolean removeRecursion(T value) {
//判断是否是null
if (value == null) throw new IllegalArgumentException("illegal value");
Node node = root;
int oldNum = num;
root = kill(root, value);
return oldNum > num;
}
public Node kill(Node node, T value) {
if (node == null) return null;
int judge = value.compareTo(node.value);
if (judge > 0) {
node.right = kill(node.right, value);
} else if (judge < 0) {
node.left = kill(node.left, value);
} else {
Node tempNode = node.right;
//双节点情况
if (node.left != null && node.right != null) {
while (tempNode.left != null) {
tempNode = tempNode.left;
}
node.value = tempNode.value;
node.right = kill(node.right, node.value);
}
//单节点或者叶子节点
Node temp = node.left != null ? node.left : node.right;
size--;
return temp;
}
return node;
}
需要注意的点:
- 与增加的递归方法一样,需要有两个方法,第一个方法的作用主要是把root塞入第二个方法中,并且判断是否删除成功
- 在双节点的删除中可以在赋值后再次调用这个删除方法完成后续的删除过程
- 单边节点与叶子节点的删除与常规方法几乎一样
前序遍历
常规方式
public List<T> preOrder1() {
//用集合类来存储遍历
List<T> list = new ArrayList<>();
//通过栈的操作来进行遍历
Stack<Node> stack = new Stack<>();
stack.push(root);
//遍历的方式为,出栈一个,就进栈其右左子节点,注意进栈顺序
while (!stack.isEmpty()) {
Node pop = stack.pop();
list.add(pop.value);
if (pop.right != null) stack.push(pop.right);
if (pop.left != null) stack.push(pop.left);
}
return list;
}
需要注意的点:采用栈的方式,不是完全进栈和出栈,而是出栈进栈相结合的方式来达到遍历,此外,进栈出栈的顺序也很重要,由于前序的遍历是前左右,根据栈的特性,先进后出,所以left需要后进
递归方式
public void preOrder2(List<T> list, Node node) {
if (node == null) return;//出口
list.add(node.value);
preOrder2(list, node.left);
preOrder2(list, node.right);
}
需要说明的是:list.add(node.value);的位置十分重要,他决定了遍历的顺序,因为是前序遍历,所以先存进去的是根,所以要放在第一句。
中序遍历
常规方法
public List<T> inOrder(){
List<T> list = new ArrayList<>();
Stack<Node> stack = new Stack<>();
Node node = root;
while (!stack.isEmpty()|| node != null){
while (node != null){
stack.push(node);
node = node.left;
}
Node pop = stack.pop();
list.add(pop.value);
node = pop.right;
}
return list;
}
需要注意的点:
- 两个循环的作用,由于中序遍历是左中右,则优先遍历左子树,所以先将每个节点的左子树入栈再出栈
- 第一个循环的条件为
!stack.isEmpty()|| node != null,即两个条件都不满足的时候才终止循环
递归方法
public void inOrder2(List<T> list, Node node) {
if (node == null) return;
preOrder2(list, node.left);
list.add(node.value);
preOrder2(list, node.right);
}
后序遍历
常规方法
public List<T> postOrder() {
List<T> list = new ArrayList<>();
Stack<Node> stack = new Stack<>();
Node node = root;
stack.push(node);
while (!stack.isEmpty()) {
Node pop = stack.pop();
list.add(0, pop.value);
if (pop.left != null) {
stack.push(pop.left);
}
if (pop.right != null) {
stack.push(pop.right);
}
}
return list;
}
需要注意的点:
- 后序遍历与前序遍历的程序十分相似,但是后续遍历主要不同点在于
list.add(int index,T value)的应用 - 最后判断
pop.left和pop.right的两个if必须分开写,不可写作if……else if
递归方法
public void postOrder2(List<T> list, Node node) {
if (node == null) return;
postOrder2(list, node.left);
postOrder2(list, node.right);
list.add(node.value);
}
根据前序遍历和中序遍历建树
public Node buildByPreInOrder(List<T> preOrder, List<T> inOrder) {
if(inOrder.size() == 0) return null;
if(inOrder.size() == 1) return new Node(inOrder.get(0), null,null);
Node node = new Node(preOrder.get(0), null, null);
int index = inOrder.indexOf(preOrder.get(0));
List<T> inLeft = inOrder.subList(0, index);//左闭右开
List<T> inRight = inOrder.subList(index + 1, inOrder.size());//左闭右开
List<T> preLeft = preOrder.subList(1,index + 1);//左闭右开
List<T> preRight = preOrder.subList(index + 1,preOrder.size());//左闭右开
node.right = buildByPreInOrder(preRight, inRight);
node.left = buildByPreInOrder(preLeft, inLeft);
return node;
}
需要注意的点:
-
此方法中未提供最终size的值,如果需要,则可以额外给size赋值,即
size = preOrder.size() -
通过subList划分开区间为左闭右开,因此需要对左右坐标做微处理
-
只能通过前序和中序,后序和中序,不可以通过前序和后序来建树,因为前序和后序只能确定根节点位置,无法确定其他的点位置
根据后序遍历和中序遍历建树
public Node buildByPostInOrder(List<T> postOrder, List<T> inOrder) {
if (inOrder.size() == 0) return null;
if (inOrder.size() == 1) return new Node(inOrder.get(0), null, null);
Node node = new Node(postOrder.get(postOrder.size() - 1), null, null);
int index = inOrder.indexOf(node.value);
List<T> inLeft = inOrder.subList(0, index);
List<T> inRight = inOrder.subList(index + 1, inOrder.size());
List<T> postLeft = postOrder.subList(0, index);
List<T> postRight = postOrder.subList(index, postOrder.size() - 1);
node.right = buildByPostInOrder(postRight, inRight);
node.left = buildByPostInOrder(postLeft, inLeft);
return node;
}
几乎与前序加中序建树一模一样。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号