论文阅读2025.10.22 ：Constrained Decoding for Robotics Foundation Models

这篇文章是CMU和Toyota InfoTech Lab联合发布的，之前看过一些这个丰田实验室关于时序逻辑的论文（IJRR），印象很深，所以格外关注了这一篇。这是投稿到ICLR上面的文章

文章的网站在https://constrained-robot-fms.github.io/。

端到端模型是这两年比较火热的方向。但是这些模型仍然是数据驱动的，用通俗的话来说就是缺乏可解释性。为了搞定这种所谓的“可解释性”，人们通常会使用形式化语言来描述任务，然后如何使用这种形式化语言通常是一篇paper的重点。那么这篇文章呢用的是比较新颖的方法，引入了一个受限解码框架来解决上面的问题。

1.建模

首先把文章的问题进行数学建模。

1.1 信号时序逻辑 Signal Temporal Logic (STL)

信号时序逻辑是一种描述水平比较高的形式化语言。与LTL不同的是，它处理的是连续的信号而非离散的原子命题（atomic proposition），同时加入了连续的时间限制而非仅仅是时序上的约束。

具体地说，\((s,t)\models \phi\) 表示信号\(s\)在时刻\(t\)满足STL规范 \(\phi\) 。STL规范的原子谓词形式使用不等式 \(\mu(s(t)) \geq 0\) 来表示，也就是说这个值如果是正的就代表原子命题是真的。从语法（syntax）上来说，STL定义如下：

\[\phi := \mu \mid \neg \mu \mid \phi \wedge \psi \mid \phi \vee \psi \mid \mathbf{G}_{[a,b]} \psi \mid \mathbf{F}_{[a,b]} \psi \mid \phi \mathbf{U}_{[a,b]} \psi \]

给定一个 \(t\) 时刻的信号 \(s_t\)，满足\(s_t\models\phi\)布尔语义定义如下：

\[\begin{aligned} s_t &\models \mu \Longleftrightarrow \mu(s(t)) > 0 \\ s_t &\models \neg \varphi \Longleftrightarrow \neg (s_t \models \varphi) \\ s_t &\models \varphi_1 \wedge \varphi_2 \Longleftrightarrow (s_t \models \varphi_1) \wedge (s_t \models \varphi_2) \\ s_t &\models \mathbf{F}_{[a,b]}(\varphi) \Longleftrightarrow \exists t' \in [t+a, t+b] \text{ s.t. } s_{t'} \models \varphi \\ s_t &\models \mathbf{G}_{[a,b]}(\varphi) \Longleftrightarrow \forall t' \in [t+a, t+b] \text{ s.t. } s_{t'} \models \varphi \end{aligned} \]

除开STL的布尔语义之外，更加新颖的方法往往会使用表现能力更加强的定量语义，使用一个实数值来衡量当前的鲁棒值(stl robustness)，和时序逻辑的各项运算符的运算如下：

\[\begin{aligned} \rho(s_t, \mu_c) &= \mu(x_t) - c \\ \rho(s_t, \neg \varphi) &= - \rho(s_t, \varphi) \\ \rho(s_t, \varphi_1 \wedge \varphi_2) &= \min(\rho(s_t, \varphi_1), \rho(s_t, \varphi_2)) \\ \rho(s_t, \mathbf{F}_{[a,b]}(\varphi)) &= \max_{t' \in [t+a, t+b]} \rho(s'_{t'}, \varphi) \\ \rho(s_t, \mathbf{G}_{[a,b]}(\varphi)) &= \min_{t' \in [t+a, t+b]} \rho(s'_{t'}, \varphi) \end{aligned} \]

1.2 Transformer中的约束解码(constrained decoding)

很多基于transformer的自回归模型通过在每个时间步上产生model vocabulary的概率分布。这个概率分布其实就是最后一个hidden layer过一层softmax产生的。之后在解码过程中选择最有可能性的结果。在经典的解码过程中，这种最大化通过贪婪算法或者使用贝叶斯搜索来实现。但是这样往往会导致输出结果的重复性偏高，因此更普遍的做法是使用sampling的方法增大输出的多样性。

文章在这里使用了constrained decoding，用非线性的方法修剪了概率选择，来确保输出的序列满足预定义的约束条件，这里说的约束条件通常是语法上的。如果用数学语言表达的话，可以表示为最大化输出序列 subject to a constraint \(\mathcal{C}:\argmax_{y\in\mathcal{Y}_\mathcal{C}}P(y|x)\)，其中 \(\mathcal{Y}_\mathcal{C}\) 是满足 \(\mathcal{C}\)的序列集合。

1.3 Problem Formulation

考虑离散的动态系统，states为\(x_t\in \mathbb{R}^n\), action为\(a_t\in\mathbb{A}\)，系统的动态方程为\(x_{t+1}=f(x_t,a_t)\)，系统的控制策略根据每个时间步的observation和task context来输出action。我们将控制策略的所有输入整合成一个多模态输入\(\mathcal{I}_t\)，这个输入首先通过编码进入到一个 embedding space：\(e_{\mathcal{I}_t}=\mathcal{E}_\mathcal{I}(\mathcal{I}_t)\)

在已知从0到t时刻的encoded inputs，需要使用一个基于transformer、参数记为\(\theta\)的foundation model来预测下面\(T-t\)个actions：

\[\{ \hat{e}_{a_{t+k}} \}_{k=1}^{T-t} = \mathrm{Transformer}_{\theta} ( \{ e_{\mathcal{I}_{\tau}} \}_{\tau=0}^{t} ). \]

每个输出的action embedding又被解码为 \(\hat{a}_{t+k}\in\mathbb{A}\)。下面考虑给定的任务规范STL公式 \(\varphi\) ，从数学语言上来说，需要满足下面的规范：

\[\{ (x_0, \hat{a}_0), \dots, (x_T, \hat{a}_T) \} \models \varphi \]

当前主流的方法都是通过filter或者直接删掉不合理的actions，但是这样会存在两个问题：一是模型的学习分布失真，从而导致输出并不合理；二是简单删除的操作可能会导致hidden state中因果链被破坏，因此主要考虑的问题就是：如何在RFM的动作生成中强制执行STL规范，是输出序列满足规范的哦那个是忠实于模型的自回归分布(autoregressive distribution) \(\pi(a_{1:T}|\mathcal{I}_{1:T})\)

理想的情况下，constrained distribution可以表示为：

\[Q_{\pi, \varphi}(a_{1:T}) = \frac{\pi(a_{1:T}) \cdot \mathbf{1}[(x_{1:T}, a_{1:T}) \models \varphi]}{\sum_{a'_{1:T}} \pi(a'_{1:T}) \cdot \mathbf{1}[(x'_{1:T}, a'_{1:T}) \models \varphi]} \tag{1} \]

这项工作的主要目标就是找到 \(Q_{\pi, \varphi}\) ，来保证完成规范并忠于原始模型的preference。

2. 规范引导的约束解码(Specification-Guided Constrained Decoding)

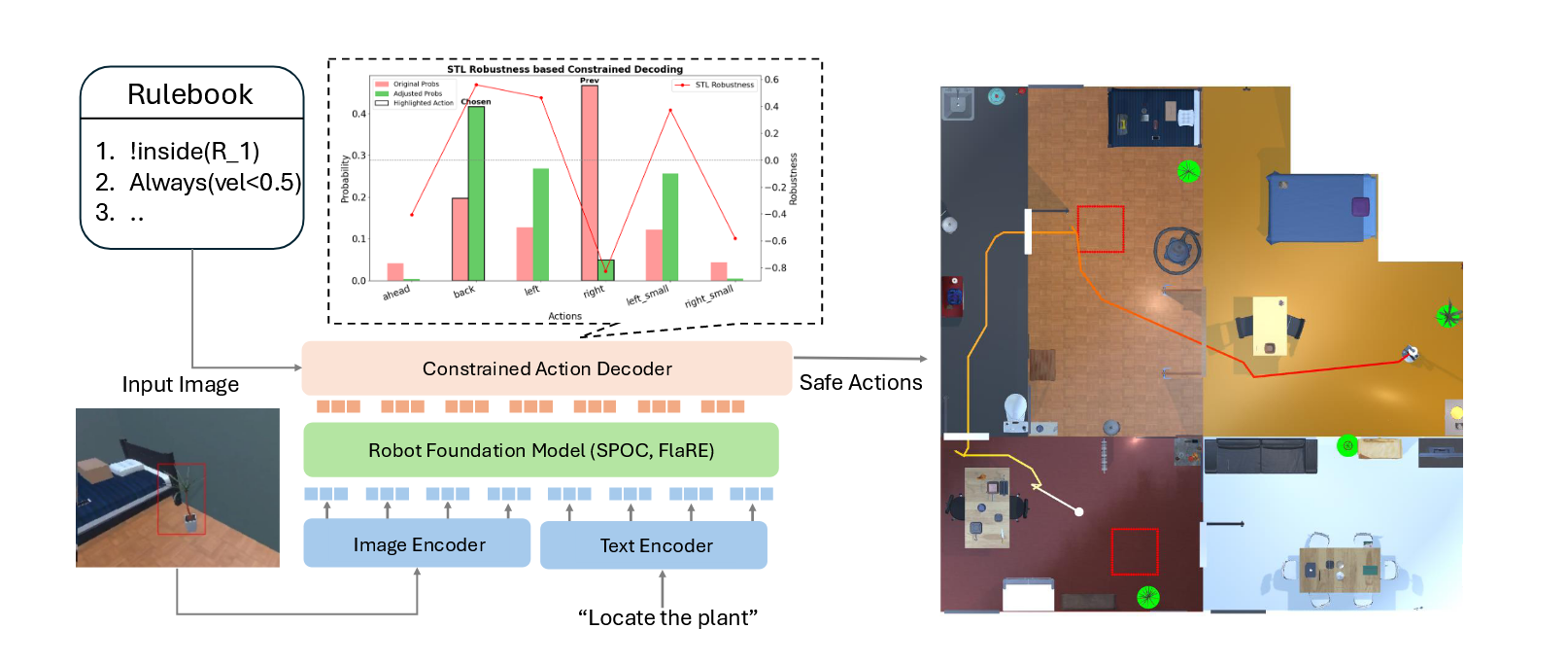
这是文章提出方法的pipeline。给定多模态输入，预训练的机器人模型(Robot Foundation Model, RFM)生成action，这些action基于时序逻辑的约束解码进行调整。

2.1 硬约束解码(Hard Constrained Decoding，HCD)

之前提到过，网络的输出层通过embeddings转换成logits，这些logits之后又通过softmax转换成概率分布。在一些NLP的工作中，往往会剔除掉invalid的输出，这种剔除通常是把他们的logits value设置为\(-\infin\)来实现的。在HCD中我们使用一种类似的方法作为constrained decoding literature。

下面我们介绍一下如何使用数学语言完成HCD：

给定在\(t+k\)时间步的logits向量 \(\mathbf{z}_{t+k}\)，对于每个动作对应的 \(z_{t+k}^{(i)}\)

\[z_{t+k}^{(i)} = \begin{cases} -\infty, & \text{if } \hat{x}_{t+k}^{(i)} = f(x_{t+k-1}, \hat{a}_{t+k}^{(i)}) \text{ violates } \varphi \\ z_{t+k}^{(i)}, & \text{otherwise} \end{cases} \]

2.2 鲁棒值约束解码(Robustness Constrained Decoding, RCD)

经过实验，hard-filtering的HCD会导致较低的任务成功率。为了解决这种问题，文章提出RCD，使用STL Robustness衡量任务的完成程度。RCD 通过结合反映\(\varphi\)满意度的robustness，软性地引导模型采取更符合任务规范的行动。

robustness value通过实值函数\(\rho(x_t,\varphi)\)来衡量，如果是正值就代表符合规范，否则则代表违反。

首先针对每个候选动作，计算其发挥作用后的robustness score: \(r^{(i)}_{t+k}=\rho(\hat{x}_{t+k}^{(i)},\varphi)\), 该值衡量了每个候选动作满足任务规范的程度。

这个值接下来经过一层指数缩放(exponential scaling): \(w_{t+k,i}=\exp(\alpha\cdot r_{r+k,i})\)，这里\(\alpha\)是一个temprature parameter，得到一系列动作权重(action weights)。

使用这些动作权重来修正初始的logits：\(\tilde{z}_{t+k,i}=z_{t+k,i}+\beta\cdot w_{t+k,i}\)，其中\(\beta\)就是一个超参数。最后，把修正logits再过一次softmax: \(p_{t+k}=\text{softmax}(\mathbf{\tilde{z}}_{t+k})\)

3.实验

这边介绍一下实验的各项工具：

• simulator使用的是AI2-THOR
• 用了一种比较sota的navigation modelSPOC
• 编码STL使用的是STLCG++

有三个主要的性能指标metrics：

• STL Satisfaction Rate (STL St)
• Task Success rate (SR)
• Average Robustness Score (AR)

带着下面的问题进行实验：

• RCD和HCD的表现是否超过了（outperform）没有约束的model
• RCD 和 HCD 是否会导致与无约束技术相当的任务成功率
• RCD 在任务成功率方面是否比 HCD 表现更好？

最终实验的结果如下：

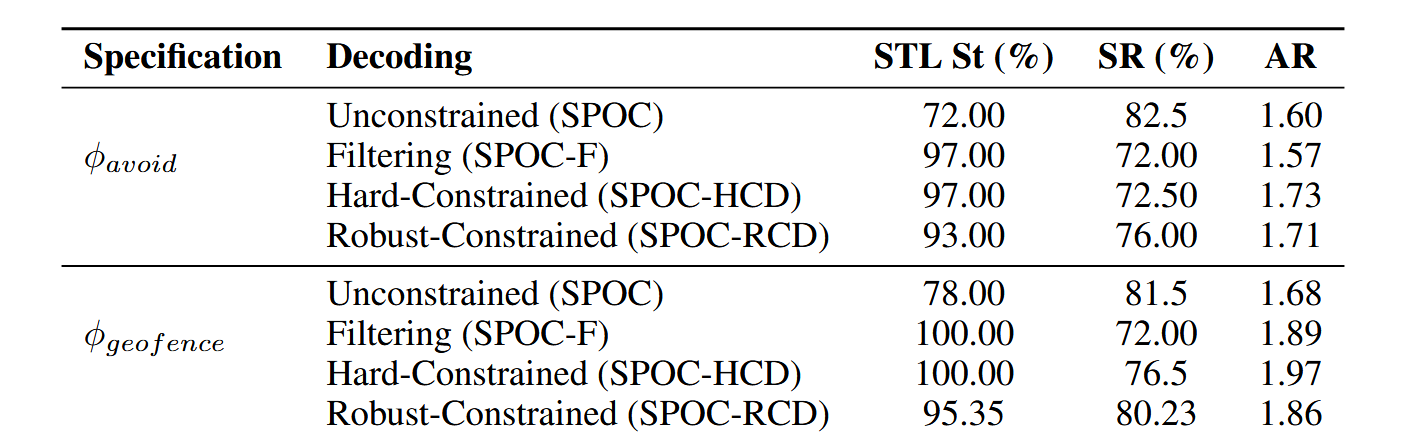
但是文章还是存在一些问题的，首先假设可以访问状态空间上定义的规范，这种规范从哪来？希望可以通过大语言模型生成（我们希望通过利用开放世界安全规范来解决这一瓶颈，利用最近在嵌入基于空间的逻辑（ETL）方面的工作[32]，并使用大型语言模型自动生成高级规范[33]）其次希望能够学习底层的世界模型