LeetCode979. 在二叉树中分配硬币

问题：979. 在二叉树中分配硬币

给定一个有 N 个结点的二叉树的根结点 root，树中的每个结点上都对应有 node.val 枚硬币，并且总共有 N 枚硬币。

在一次移动中，我们可以选择两个相邻的结点，然后将一枚硬币从其中一个结点移动到另一个结点。(移动可以是从父结点到子结点，或者从子结点移动到父结点。)。

返回使每个结点上只有一枚硬币所需的移动次数。

 

示例 1：

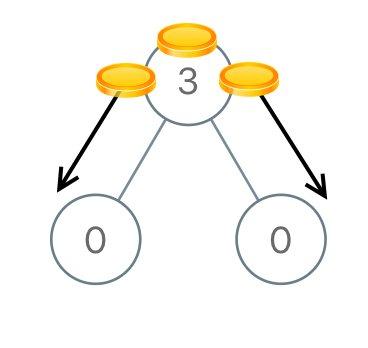
输入：[3,0,0]
输出：2
解释：从树的根结点开始，我们将一枚硬币移到它的左子结点上，一枚硬币移到它的右子结点上。

示例 2：

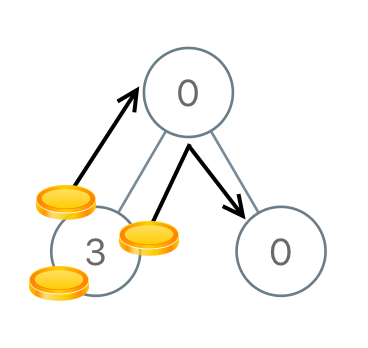
输入：[0,3,0]
输出：3
解释：从根结点的左子结点开始，我们将两枚硬币移到根结点上 [移动两次]。然后，我们把一枚硬币从根结点移到右子结点上。

示例 3：

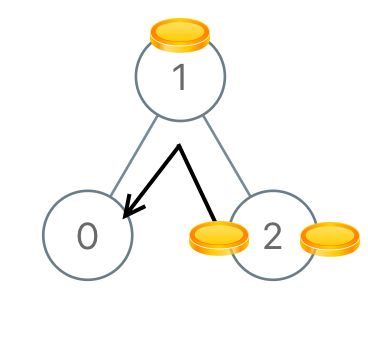
输入：[1,0,2]
输出：2

示例 4：

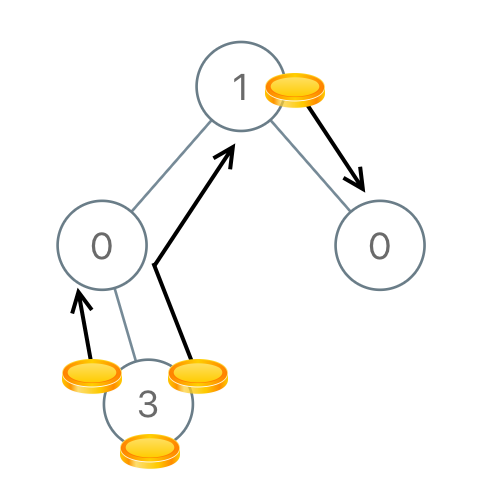
输入：[1,0,0,null,3]
输出：4

 

提示：

1. 1<= N <= 100
2. 0 <= node.val <= N

链接：https://leetcode-cn.com/contest/weekly-contest-120/problems/distribute-coins-in-binary-tree/

分析：

0.每个节点硬币存在如下几种流向：给父节点、给左子节点、给右子节点；

1.将左右节点看做一个整体，向上和向下流向是对称的，只需要统计一个方向的即可，而且左右节点看做一个整体，分发后在分别内部递归进行后续分发；

2.如果某个节点为空，则流动次数为0；

3.如果某个节点不为空，左节点节点数Node1，硬币数Coins1，右节点数Node2，硬币数Coins2，由于节点数和硬币数一致，所以差值的绝对值即需要的流动次数，即父节点给左节点的X个硬币加上父节点给右节点的Y个硬币是这一层的流动次数

4.分别计算左右节点的移动次数，累加即为结果。

 

AC Code：

 

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    //每一个节点都有接受上传下发的需求，只统计单向的即可
    //对于单个节点来说，递归
    int distributeCoins(TreeNode* root) {
        int ret = 0;
        if (root == NULL)
        {
            return 0;
        }
        else
        {
            int tmpleftnodes = 0;
            int tmpleftconins = 0;
            int tmprightnodes = 0;
            int tmprightcoins = 0;
            int tmpselfnode = 0;
            int tmpselfcoins = 0;
            GetInfo(root, tmpleftnodes, tmpleftconins, tmprightnodes, tmprightcoins, tmpselfnode, tmpselfcoins);

            int tmpdeltaleft = tmpleftconins - tmpleftnodes;
            int tmpdeltaright = tmprightcoins - tmprightnodes;
            //int tmpselfdelta = tmpselfcoins - tmpselfnode;
            int tmpselfdelta = 0;
            ret = ret + abs(tmpselfdelta - tmpdeltaleft) + abs(tmpselfdelta - tmpdeltaright);
            ret = ret + distributeCoins(root->left) + distributeCoins(root->right);
        }
        
        return ret;

    }
    //获得该节点左右节点数以及所拥有的硬币数
    void GetInfo(TreeNode* root, int& leftnodes, int& leftconins, int& rightnodes, int& rightcoins,int& selfnode,int& selfcoins)
    {
        if (root == NULL)
        {
            leftnodes = 0;
            leftconins = 0;
            rightnodes = 0;
            rightcoins = 0;
            selfnode = 0;
            selfcoins = 0;
            return;
        }
        else if (root->left == NULL && root->right == NULL)
        {
            leftnodes = 0;
            leftconins = 0;
            rightnodes = 0;
            rightcoins = 0;
            selfnode = 1;
            selfcoins = root->val;
            return;            
        }
        else //if (root->left != NULL && root->right != NULL)
        {
            int tmpleftnodes = 0;
            int tmpleftconins = 0;
            int tmprightnodes = 0;
            int tmprightcoins = 0;
            int tmpselfnode = 0;
            int tmpselfcoins = 0;
            GetInfo(root->left, tmpleftnodes, tmpleftconins, tmprightnodes, tmprightcoins, tmpselfnode, tmpselfcoins);
            leftnodes = tmpleftnodes + tmprightnodes + tmpselfnode;
            leftconins = tmpleftconins + tmprightcoins + tmpselfcoins;

            tmpleftnodes = 0;
            tmpleftconins = 0;
            tmprightnodes = 0;
            tmprightcoins = 0;
            tmpselfnode = 0;
            tmpselfcoins = 0;
            GetInfo(root->right, tmpleftnodes, tmpleftconins, tmprightnodes, tmprightcoins, tmpselfnode, tmpselfcoins);
            rightnodes = tmpleftnodes + tmprightnodes + tmpselfnode;
            rightcoins = tmpleftconins + tmprightcoins + tmpselfcoins;
            selfnode = 1;
            selfcoins = root->val;
        }
    }
    
};

 

其他：

1.由于左右均衡是通过父节点实现的，所以其实不需要看父节点的硬币数量

 

2.第一code：

typedef signed long long ll;

#undef _P
#define _P(...) (void)printf(__VA_ARGS__)
#define FOR(x,to) for(x=0;x<(to);x++)
#define FORR(x,arr) for(auto& x:arr)
#define ITR(x,c) for(__typeof(c.begin()) x=c.begin();x!=c.end();x++)
#define ALL(a) (a.begin()),(a.end())
#define ZERO(a) memset(a,0,sizeof(a))
#define MINUS(a) memset(a,0xff,sizeof(a))
//-------------------------------------------------------


class Solution {
public:
    int ret;
    pair<int,int> count(TreeNode* root) {
        pair<int,int> A={1,root->val};
        if(root->left) {
            auto a=count(root->left);
            A.first+=a.first;
            A.second+=a.second;
        }
        if(root->right) {
            auto a=count(root->right);
            A.first+=a.first;
            A.second+=a.second;
        }
        ret+=abs(A.first-A.second);
        return A;
    }
    
    int distributeCoins(TreeNode* root) {
        ret=0;
        count(root);
        return ret;
    }
};

pair记录节点个数和所拥有的硬币数，差值都是需要流动的

 

另一个code：

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 
 class Solution {
public:
    int sgn(int x) {
        if (x == 0)
            return 0;
        return x < 0 ? -1 : 1;
    }
    int maxTurbulenceSize(vector<int>& A) {
        int n = A.size();
        int l = 0;
        int ans = 1;
        for (int r = 1; r < n; ++r) {
            if (l + 1 < r and sgn(a[r] - a[r - 1]) == sgn(a[r - 1] - a[r - 2])) {
                l = r - 1;
            }
            if (a[r] == a[r - 1]) {
                l = r;
            }
            ans = max(ans, r - l + 1);
        }
        
        return ans;
    }
};

 */


class Solution {
public:
    int sz(TreeNode* root) {
        if (root == nullptr)
            return 0;
        return 1 + sz(root->left) + sz(root->right);
    }
    
    int coins(TreeNode* root) {
        if (root == nullptr) {
            return 0;
        }
        
        return root->val + coins(root->left) + coins(root->right);
    }

    int distributeCoins(TreeNode* root) {
        // number of coins over edge = diff between coins and nodes for each subtree
        if (root == nullptr) {
            return 0;
        }
        return abs(coins(root) - sz(root)) + distributeCoins(root->left) + distributeCoins(root->right);
    }
};