青岛oj集训9

最小生成树——Prim

生成树的过程：类似dijk，从1开始，每次加一个点，保证联通。

先存边

记录每一个点ismst：即vis，记录每个点是否在最小生成树中

每次选择一个ismst=0的点

再记录lowcost[i]：i与 已经在最小生成树中的点 的所有连边中的最小值

每次加入新的点加入树时，把与之相邻的所有点都更新lowcost

每次选择所有ismst=0的点中lowcost最小的点

如果所有ismst=0的点的lowcost都=inf，则该图无最小生成树

时间复杂度：算法执行n-1次，每次枚举所有点n，再加上所有边只会被遍历一次

所以O（n^2+m）

初始化：lowcost[i]=inf，ismst[i]=0，ismst[1]=1;

设最开始从1开始更新，即p=1

然后松弛其所有临边

再寻找下一个点

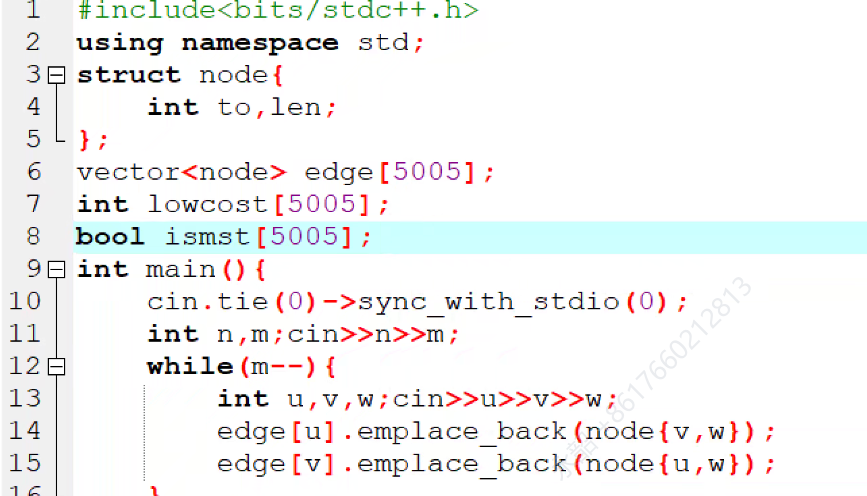
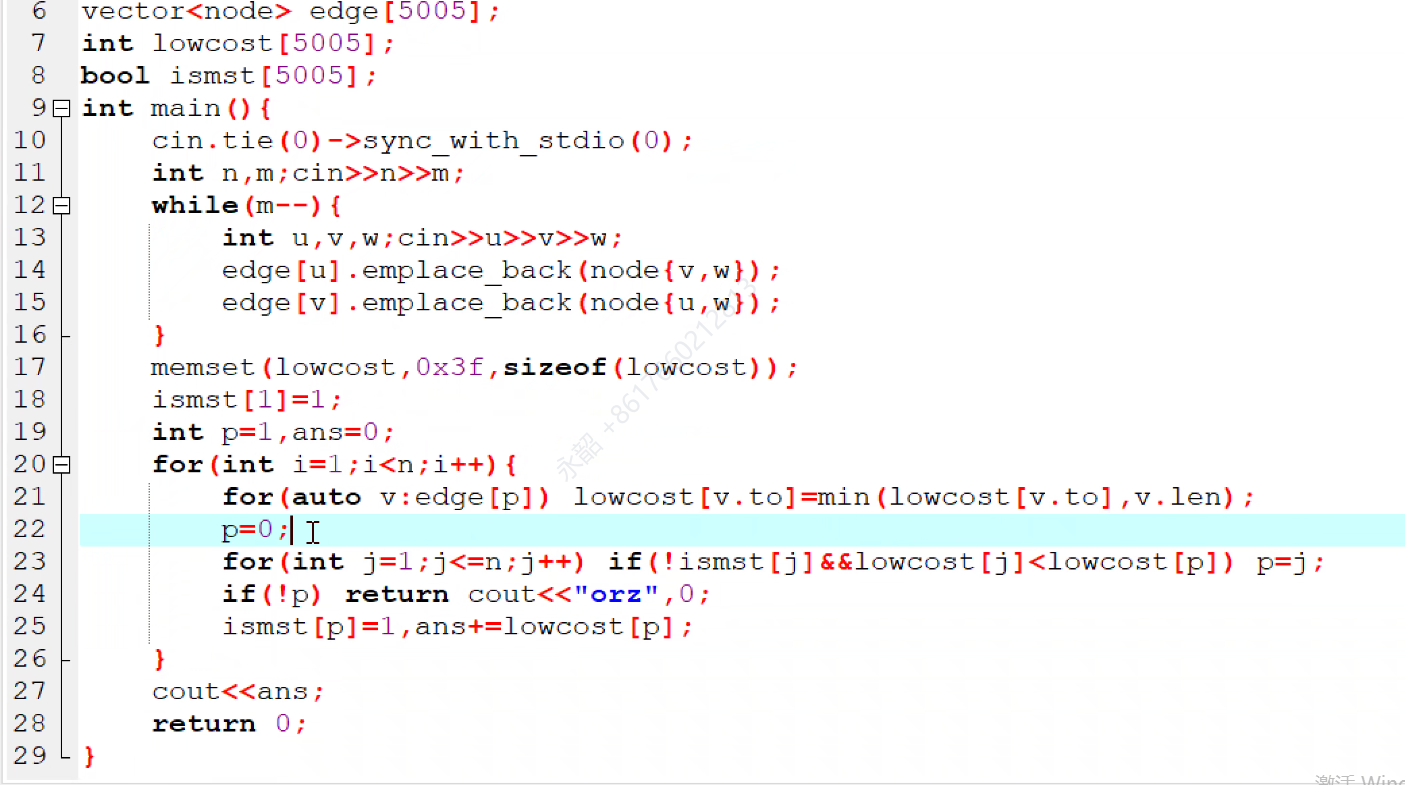
Prim和Dijk很像

因为每次都要松弛，O(m)很小，但每次暴力枚举都要O(n^2)

但是Dijk可以进行队列优化

所以Prim也能队列优化

但是普遍认为Prim队列优化没有任何用处

因为kruskal算法的复杂度是O(m log m)

所以Prim只有在m=n^2时才优于kruskal

而且kruskal有限制

1265

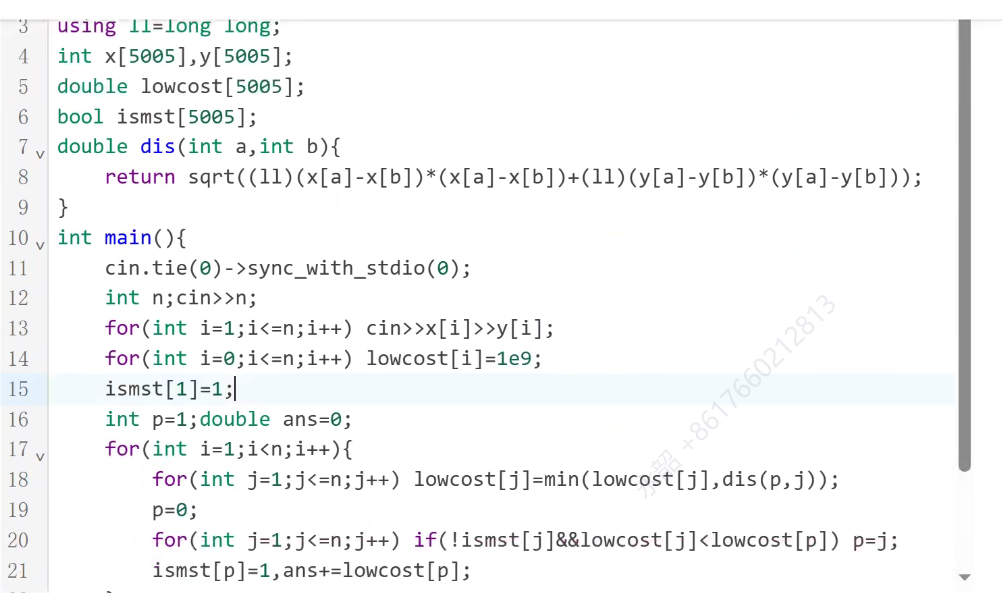
典型的只能用Prim，不能用kruskal

2573

有向边的最小生成树（外向树）

可以近似看做一张DAG

因为n很大，所以要用队优化Prim

也可以先高度·从大到小，再边权从小到大排序用kruskal

2323