青岛oj集训7

并查集

1.P3367 【模板】并查集 - 洛谷

初始赋值：把所有fa[i]=i（f[i]:i的父亲）

并查集合并原理：

将a所在集合与b所在集合合并：

相当于把a所在集合的根节点所在集合与b所在集合的根节点所在集合合并

也就是把a的根节点设成b的根节点的父亲就行。

问题：若a与b本来就在同一个集合，那么将这两个合并实际就是没有事发生

也就是fa[根]=根，和初始赋值一样，也就没必要了（做了也没事）

并查集查询原理：

如果一个点不是根节点，那么去查找他的父亲，知道找到根节点

如果两个点的根节点相同，则在同一个集合

否则不在同一个集合

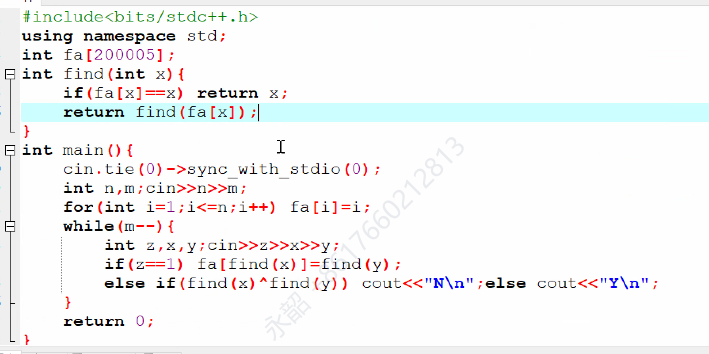
优化1：路径压缩O（mα（n））(最坏情况：O（m log n）)

改变fa[i]定义：fa[i]：i点的父亲=》fa[i]：i所在集合的根节点（把父亲变成根节点）

每次查询都会更新新的f[i]，这样find函数一步就能到位

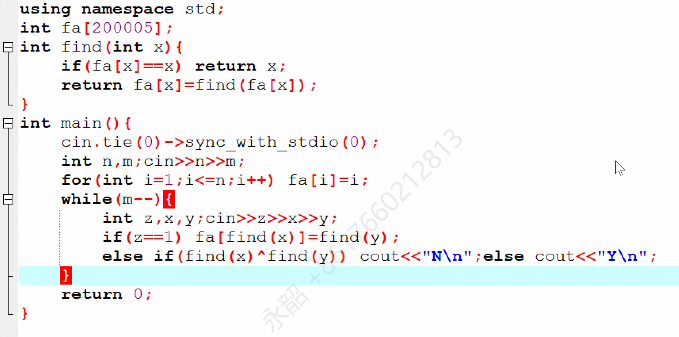
优化二：按秩合并O（m log n）：按照秩序合并（当题目中必须保留树的形态时用）

若有两棵树，高度分别为x，y；

那么把x加到y的下面和把y加到x下面没有本质区别

如果把x加到y的下面，则新的树的高度是max（x+1，y）

把x合并到y上时，复杂度是x的高度

所以要复杂度尽可能地小，就要把高度小的树插到高度大的下边

这样就能使得整体复杂度最小

所以我们可以把整棵树的高度存在根节点上

每次合并时只需要把小的合向大的就行

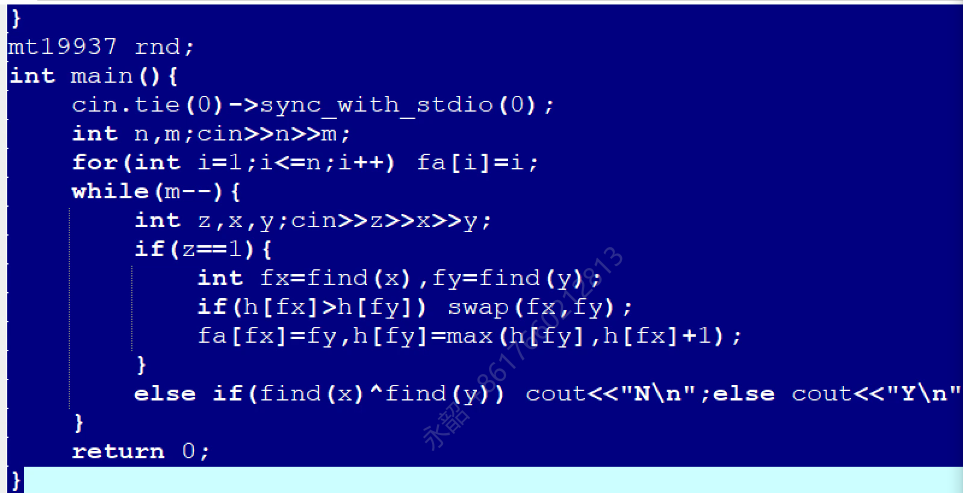
终极形态：按秩合并+路径压缩

 

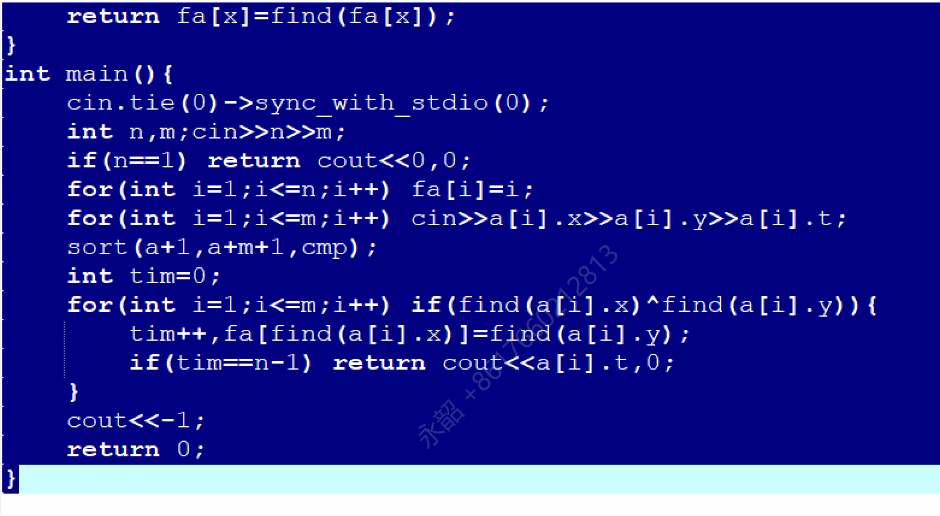
例题1：P1111 修复公路 - 洛谷

离线，排序，并查集

最终找到什么时候只剩一个联通块

当最开始所有点都是孤立的，那么需要进行n-1次有效合并才能变成一个联通块

P5937 [CEOI 1999] Parity Game - 洛谷

并查集拓展

转换成并查集来统计1的个数

抽象成图论模型：

把每一个前缀和看做一个点

如果两个点的奇偶性相同，则在同一个集合

所以最后就剩下两个集合：奇集与偶集

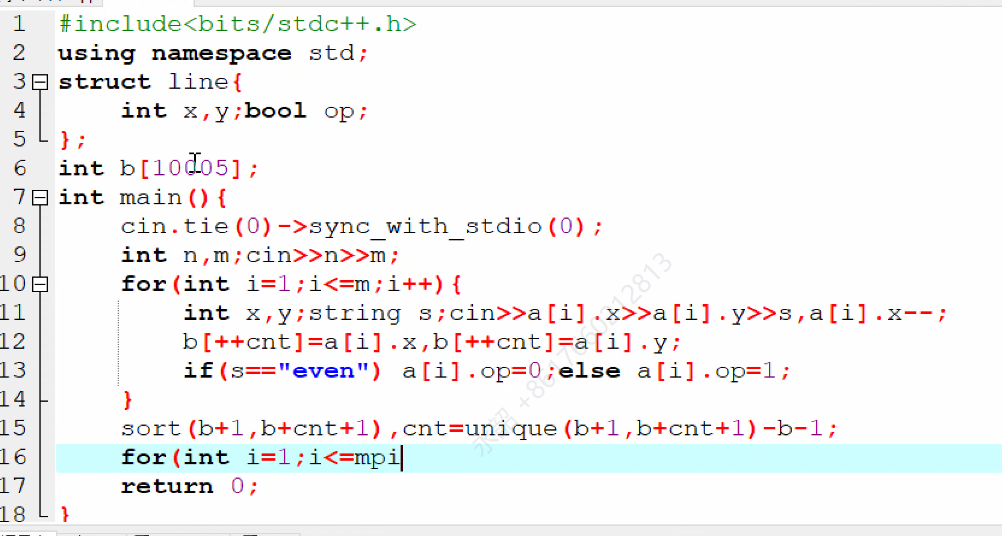
扩展域并查集：

把每个前缀和看做两个点：正点和反点

正点与反点一定不在同一集合内

那么这道题就能处理两个点不在同一集合内的情况

当两个点在同一集合内（奇偶性相同）把a正点与b正点合并，a反点与b反点合并

当两个点在不同集合内（奇偶性不同）把a正点与b反点合并，a反点与b正点合并

那么当任意一次合并后，一个点的正点和反点在同一集合内，那么这一次合并一定是不合法的（所以每次合并都要检查一遍正反不联通）

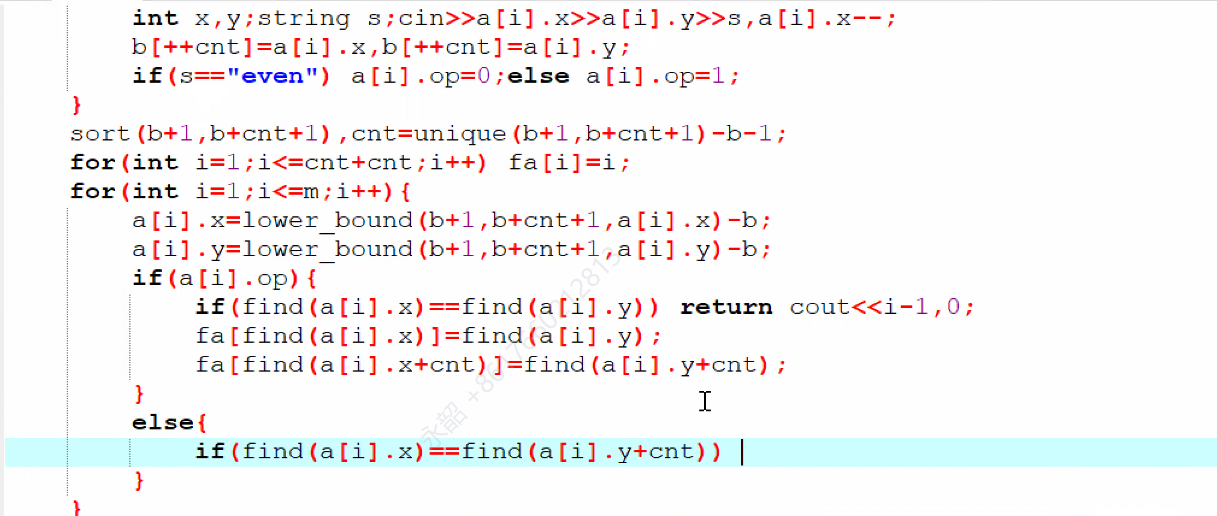
怎么检查？

当要把两个点合并到同一集合里时，要检查a正点与b反点不联通

反之，检查a正点与b正点不联通

因为如果上述条件不成立，则合并完一定会出现正反点联通，不信你试试？

此时，输出答案

这道题n过大，肯定比m大，所以要进行离散化处理

P1196 [NOI2002] 银河英雄传说 - 洛谷

带权并查集

如何初始化？

每个点有一个权值，有一个编号

初始化都是0

如何定义权值？

每一个点的权值等于这个点的编号减去父亲的编号

那么最终这个点到根节点上所有点的路径权值之和就是他的编号

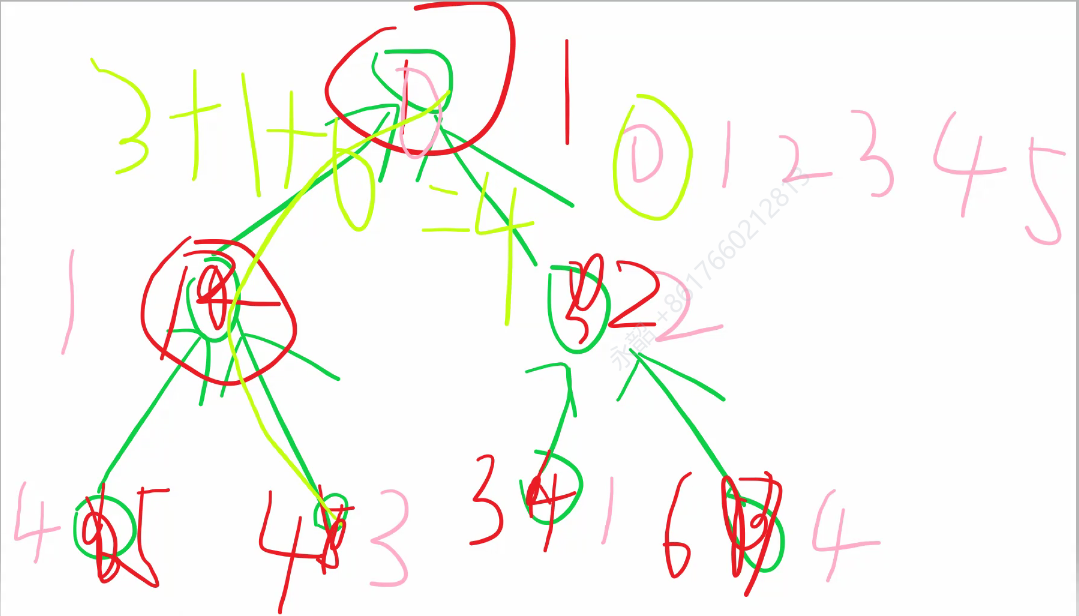
如何合并？

把新来的根节点的编号设为原集的大小，新来的点后边跟着的所有点都+=原集大小

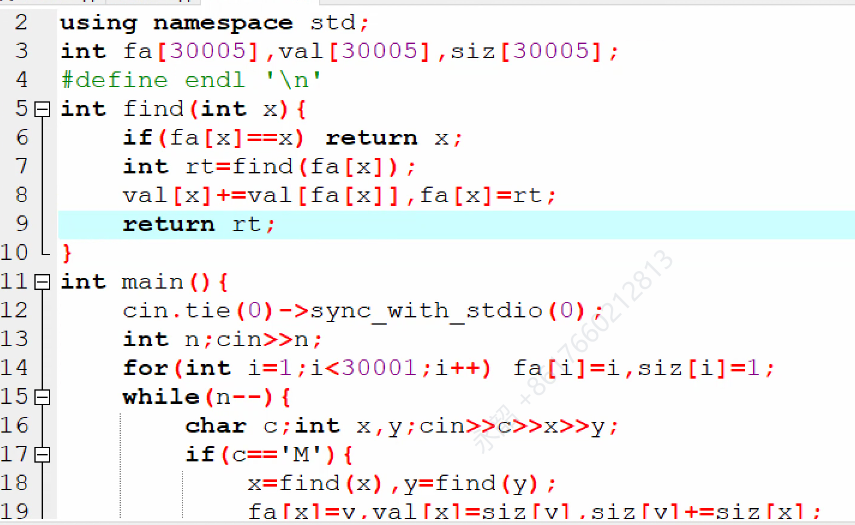
如何路径压缩？

因为把父亲变为新的父亲了，所以权值也要发生变化，要加上被删去（压缩掉）的长度

即把这个点的权值变成原来的权值+从新父亲到老父亲的编号和，即+=原父亲的权值

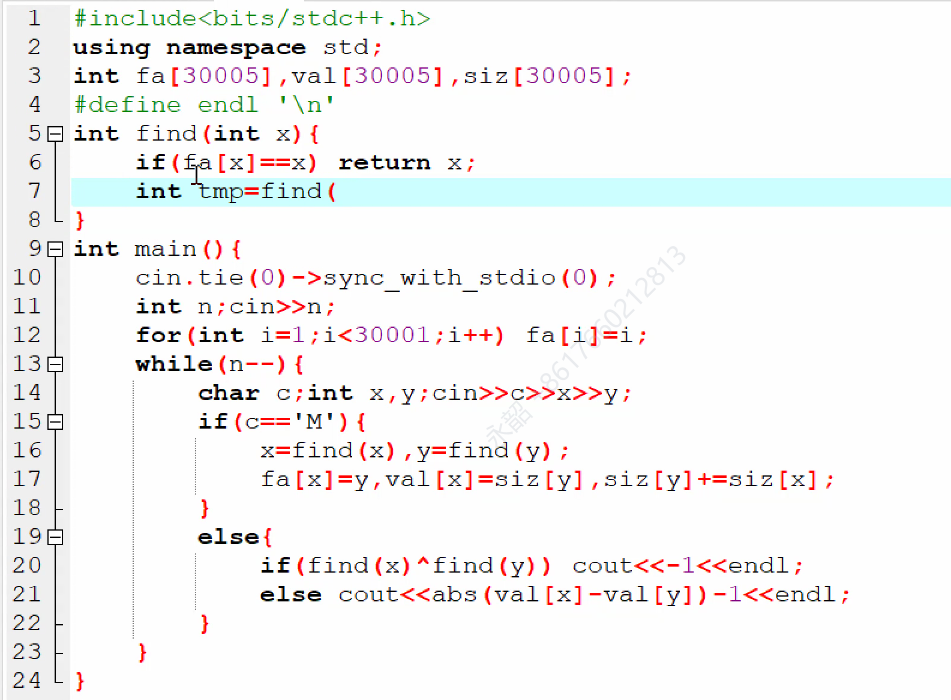
最后，回到这道题上

他问的中间有几个战舰，实际上就是问这两个点的编号之差再-1为多少