行人重识别初学(一)
主要是看b站一个链接上的视频,然后做了一些笔记,尝试对REID有一些理解
行人重识别系统
如下图所示

一般是由行人检测和行人重识别两个问题组成,这两个问题是学术界里面两个不同的研究方向,
- 比如行人检测可以用faster rcnn或者其他之类的检测框架
- 但是对于reid则是使用检测出来的行人的结果来做
所以实际上是两个不同的任务
重识别的方法
一般分为两种,一种是表征学习,一种是度量学习。表征学习就是每个人都是一个类别;度量学习旨在学习两张图片的相似性。
度量学习
将图片映射到一个新空间,然后用距离来衡量样本之间的相似性,比如欧氏距离,余弦距离。在深度学习里面,我们希望他们是可导的,这样就可以end2end的来训练。
最优的reid模型的指标是是正样本对(相同行人的两张图片)的距离尽可能小,负样本对的距离尽可能大。
欧氏距离:
对于度量学习方法而言,传统的方法都是手动提取的特征,然后学习一个最好的M,就是大家提取得到的特征(shift之类的)都是一样的,看看谁的M设计的好
感觉有点像流型学习。
在深度学习中,M是一个方阵,深度学习希望学到的是更加具有度量属性的特征。
常用的度量学习的损失有
- 对比损失
- 三元组损失
- 改进的三元组损失
- 四元组损失
- TriHard loss
对比损失
对比损失,每次要输入两张图片,然后这两张图片会进入同一个cnn网络(孪生网络),两张图片有两个特征,用对比loss进行计算,定义如下
当y=1的时候,输入的是正样本对,上述公式只有前半项,当输入y=0的时候,输入的是负样本对的时候,希望损失尽可能趋近于0,即\(d>\alpha\)的时候,才为0,即尽可能的大于某个阈值。
三元组损失
顾名思义,设计输入三张图片,三张图片分别为anchor, positive以及negative.
三张图片是有规则的。
anchor:随机挑选
positive:和anchor id一样的正样本
negative: 和anchor不一样的任意一张图片
学习的目标是尽可能拉进正样本的距离,推开负样本的距离
为了实现这个目的,需要设计一个loss,则有一个直观的loss为:
即正样本之间的间隔要小于负样本之间的\(\alpha\)的间隔
\(\alpha\)是自己设置的一个阈值。当上述公式的loss为0的时候,这个时候也意味着
这个就是loss优化的目标,作者也举了几个例子
感觉上面是有问题的,就是传统的三元组的loss和\(d_{a,p}\)的绝对值好像没有关系。这会使得loss没有绝对的值,可能会非常大,碎玉检索问题可能关系不大,因为检索问题是一个rank的问题,对于跟踪问题可能就有很大的关系。跟踪就是将所有的bbx连接起来,希望有一个绝对的距离来measure
改进的三元组loss
为了使得\(d_{a, p}\)比较好控制,在loss里面添加一项为\(d_{a, p}\),总共的loss如下
除了要约束正样本的距离要小于负样本的距离之外,还要有一个额外的约束是正样本的距离本身的绝对值尽可能小。作者举了一个例子,
对于改进三元组损失而言,\(d_{a, p}\)的绝对值是会影响这个损失的,为了优化loss,需要满足正样本的距离尽可能趋近于0,这样就能够卡阈值来跟踪判断哪些属于同一类别.所以改进三元组的loss就是添加了这么一项\(d_{a, p}\)
四元组loss
四元组loss是三元组的一个改进,输入的是四张图片,前三张图片是正常的三元组里面的图片,第四张图片是负样本,这个负样本是第三个id。也就是两个负样本是属于不容类别的id,一共四张图片,三个id。
损失有两项,第一项是和正常的三元组的loss是一样的,第二项是弱推动的三元组loss,将四张图片都利用上了
也就是负的样本也是不同的类别,也可以推开,一般的话,\(\beta<\alpha\)
第二项也可以看做也没有考虑绝对距离(演讲者自己的理解,我不太理解)
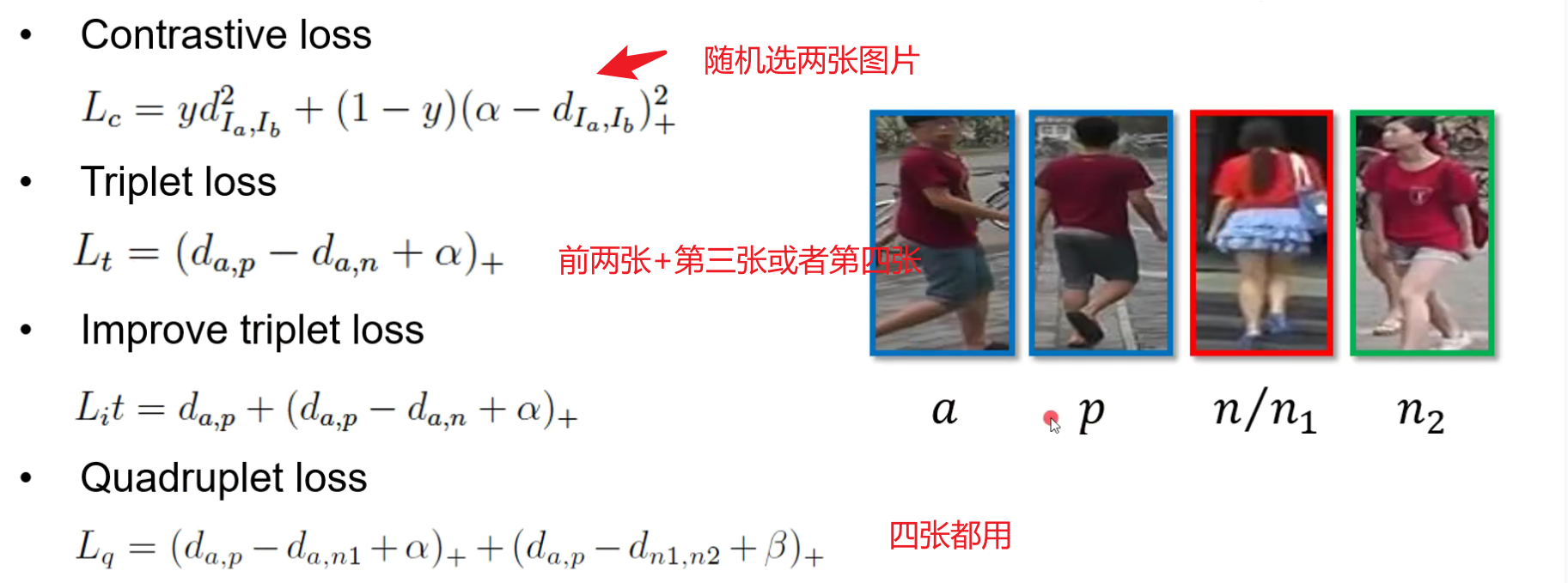
四种loss分别为:
- Contrastive loss
\(L_{c}=y d_{I_{a}, I_{b}}^{2}+(1-y)\left(\alpha-d_{I_{a}, I_{b}}\right)_{+}^{2}\)
\(L_{t}=\left(d_{a, p}-d_{a, n}+\alpha\right)_{+}\) - Improve triplet loss \(L_{i} t=d_{a, p}+\left(d_{a, p}-d_{a, n}+\alpha\right)_{+}\)
- Quadruplet loss
\(L_{q}=\left(d_{a, p}-d_{a, n 1}+\alpha\right)_{+}+\left(d_{a, p}-d_{n 1, n 2}+\beta\right)_{+}\)
四种loss总结为
难样本挖掘
传统的度量方法是随机采样组成元祖样本,但是这样采集的样本通常是一些非常容易识别的样本,不利于训练网络表达能力强的reid网络。
之前的三元组或者四元组都是随机挑选的,作者为此举了几个例子
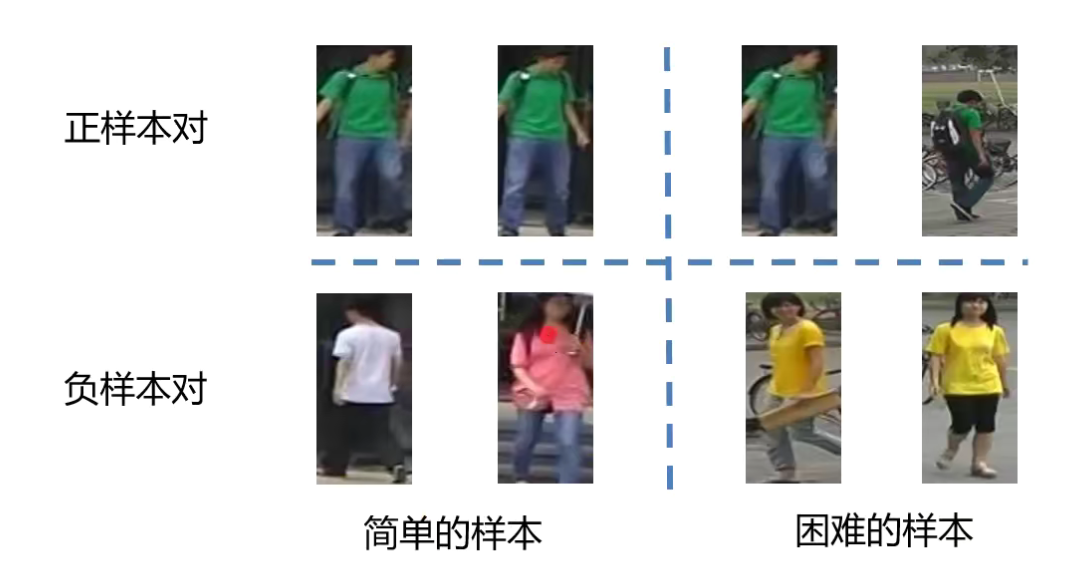
学到的结果就是对于简单的样本分的比较好,对于困难的样本就分的比较差。如果拿难的样本来训练的话,则可以增加网络的泛化性能和鲁邦能力


TriHard loss 即triplet loss with hard example mining
就是在一个batch里面挑选最难的正样本对和最难的负样本对,用这两个最难来训练网络。
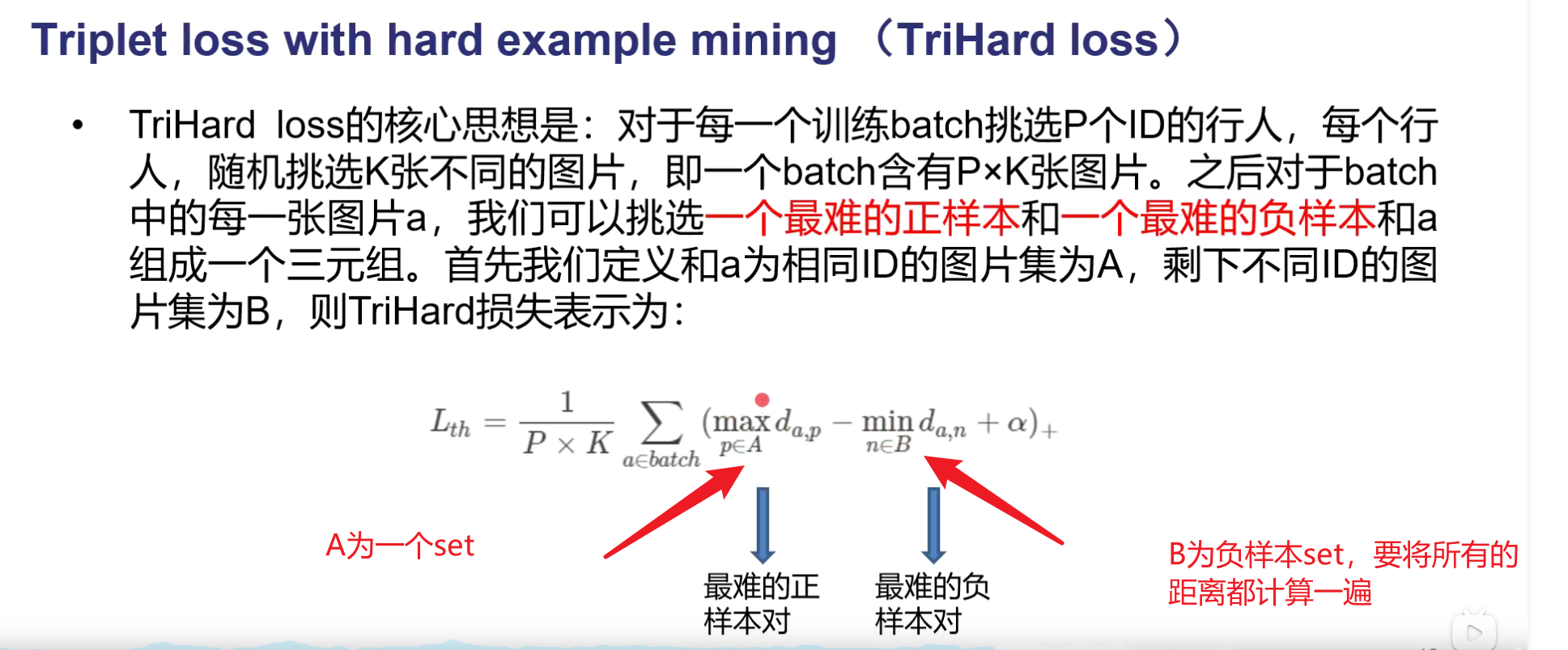
越不相似的正样本对,或者距离越大,这个时候就比较hard的正样本对。对于负样本对也一样
真正实现的时候,如下图所示:

同时作者还讲了一篇CVPR2018的文章triplet loss with adaptive weights
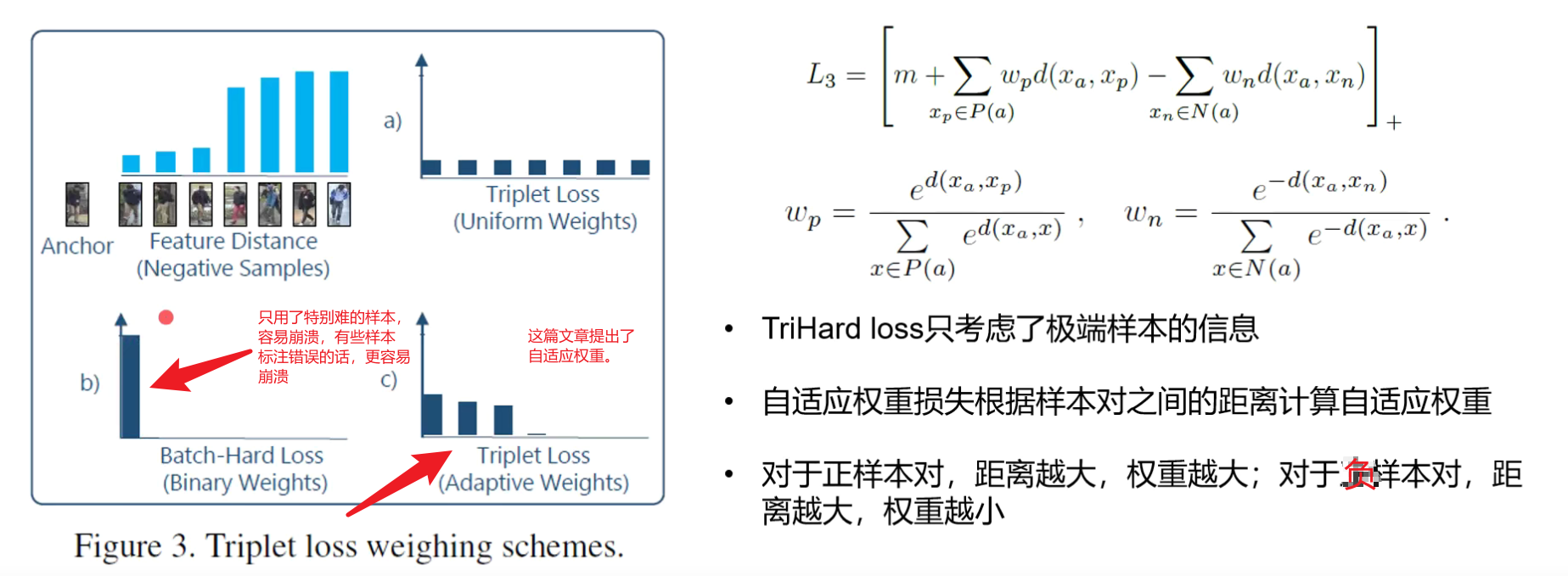
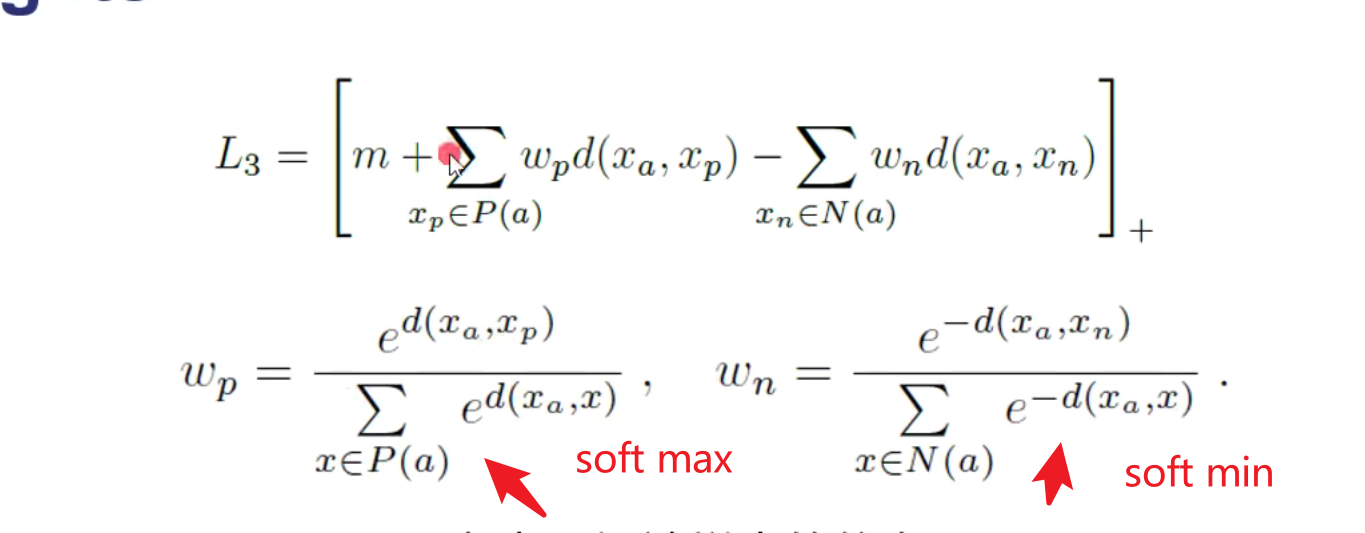
作者验证说是如果triple hard和adapt weight都能够收敛的话,他们的差距不会太大。
总结


大概是18年更新的ppt,所以triple hard loss18年之前主流
度量学习的训练结果好坏和三元组组的好坏有关系
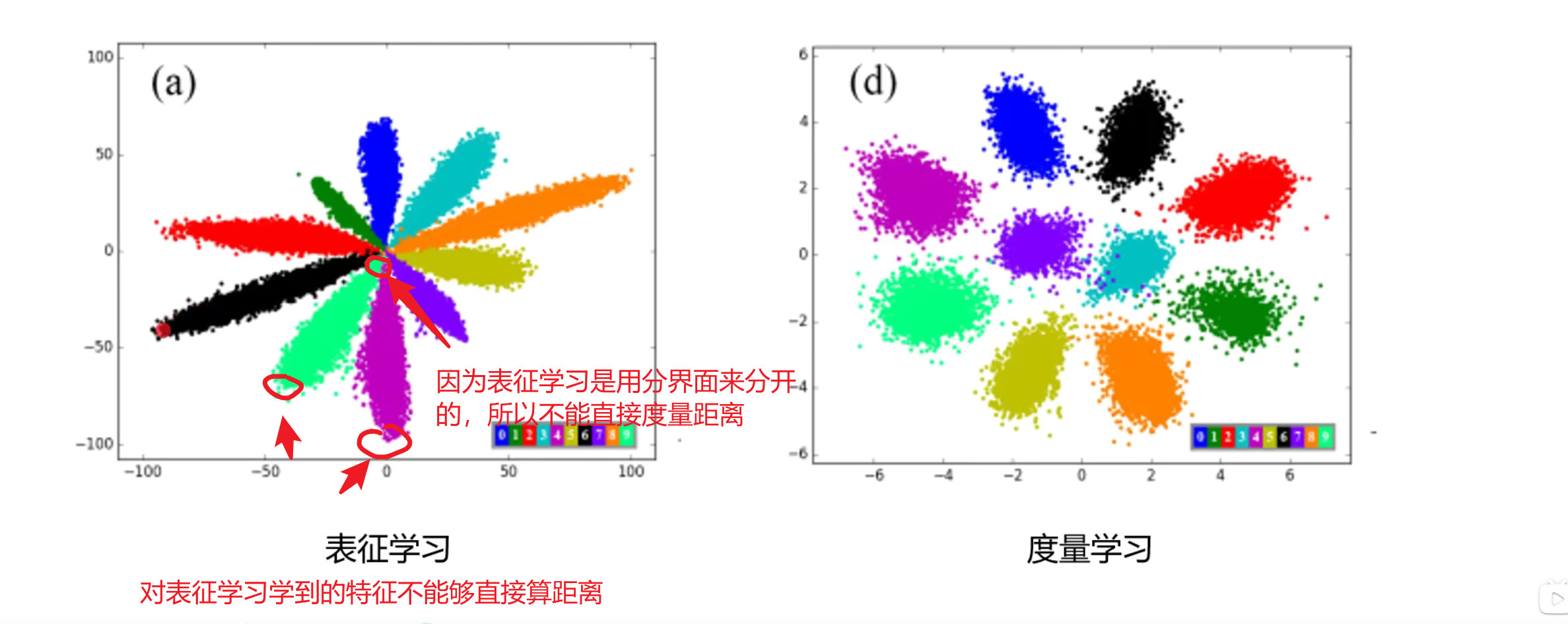
处理表征学习的方式是归一化到球面上,另外一个是计算cos的距离,计算特征之间的夹角,夹角和半径无关。
度量学习的是聚类,已经比较好的分开。
当然也可以同时做
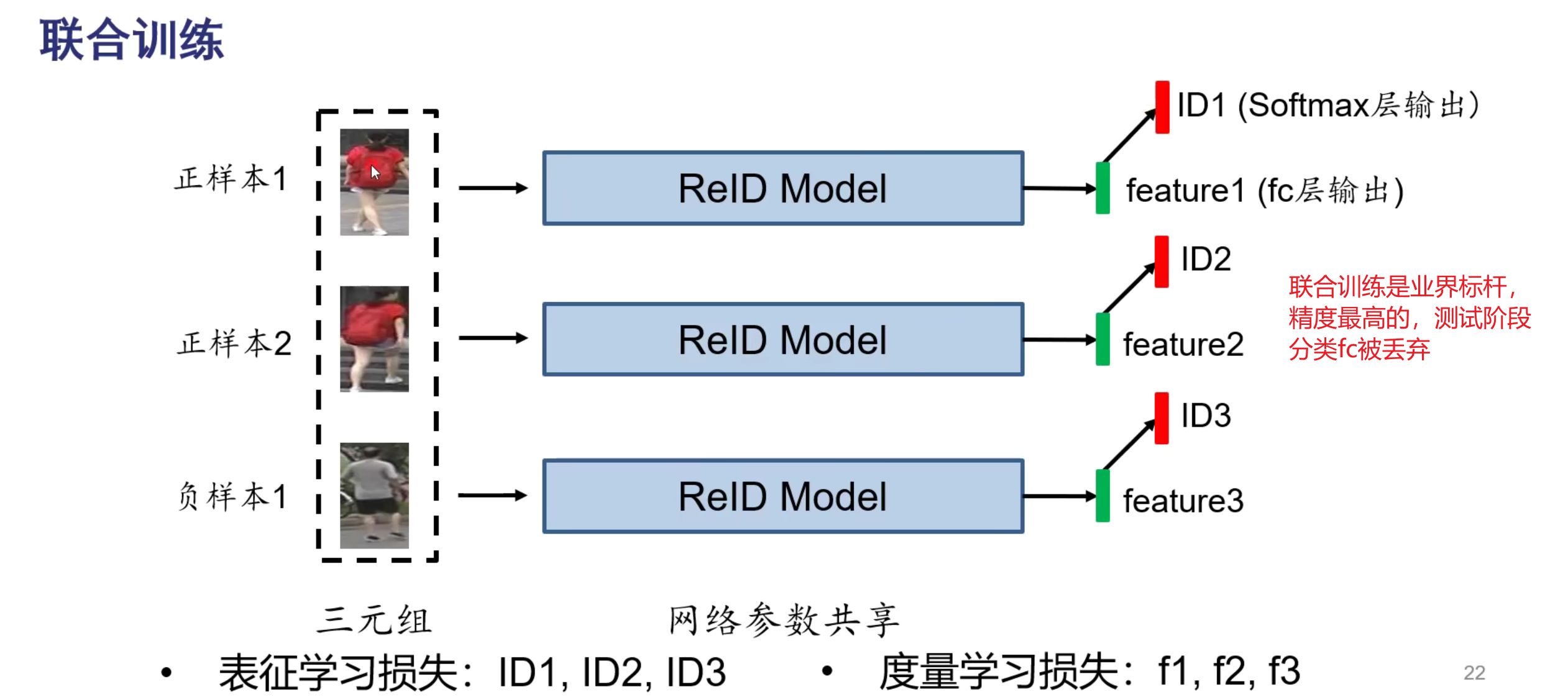
课后思考
- 是否可以改进id损失,或者是表征学习,使得能够直接学习相似性度量,参考人脸识别
posted on 2021-09-18 16:56 YongjieShi 阅读(713) 评论(0) 收藏 举报




 浙公网安备 33010602011771号
浙公网安备 33010602011771号