最短编辑距离

题干

原题链接

思路：动态规划

推导

要实现将A转换为 B，那也就是对A 进行操作，那么，我们设dp[i-1][j-1]为串A的前i-1个字符转换为B 的前j-1个字符的最少操作数，那么，如何求解dp[i][j]？求解出这个，是不是就可以通过递推求出dp[n][m]了？（这里假设A 的长度为n ，B的长度为m）,好，那我们来分析一下:

如果a[i]==b[j] ，那么是不是不用进行操作？则dp[i][j]=dp[i-1][j-1]

如果不等的话，我们要怎么办呢？那是不是要对A 进行增, 删, 改操作?然后我们取其中最小的值作为该步骤的最小操作。那我们来分析一下各种情况：

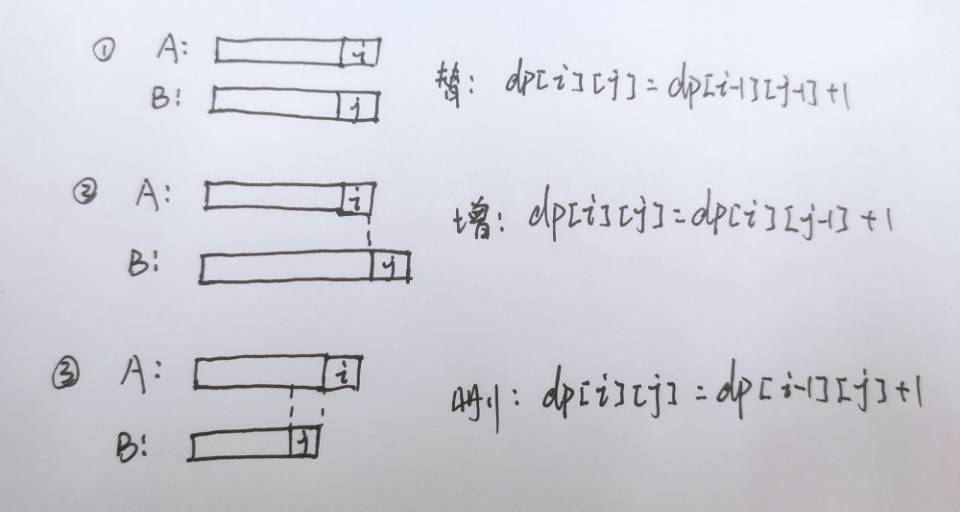
1. 替换。这种情况是不是只要将A[i]的值替换为B[j]就能使A和B相等了。所以此时的最小操作数等于i-1个长度的操作数+1，即 dp[i][j]=dp[i-1][j-1]+1
2. 增加。如图，如果A串的长度小于B串，那这时我是不是要在A串的末尾加上一个字符才能和B相等，所以操作数=A的前i个字符和B的前j-1个字符匹配的最小操作数+1，即dp[i][j]=d[i][j-1]+1
3. 删除。同上类推

初始化

dp数组的初始化就是A 为空的时候，那么A要执行的最小操作就是把B 的字符拷贝过来，即d[0][j]=j

同样的，B为空的时候，就要把A的内容删掉,dp[i][0]=1

代码

#include <bits/stdc++.h>
using namespace std;
int dp[2000 + 10][2000 + 10];
char a[2000 + 10], b[2000 + 10];
int main() {
    scanf("%s %s", a, b);
    int n = strlen(a), m = strlen(b);
    for (int i = 1; i <= n; i++) {
        dp[i][0] = i;
    }
    for (int i = 1; i <= m; i++) {
        dp[0][i] = i;
    }
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            if (a[i - 1] == b[j - 1])  //字符串数组从0开始,所以第i个字符为a[i-1]
                dp[i][j] = dp[i - 1][j - 1];
            else
                dp[i][j] =
                    min(min(dp[i][j - 1], dp[i - 1][j - 1]), dp[i - 1][j]) + 1;
        }
    }
    cout << dp[n][m];
    return 0;
}

时间复杂度：\(O(n*m)\)