kmp算法
什么是kmp算法?
kmp算法适用于解决模式匹配问题的一个优化的算法,一般是解决字符串匹配的问题。解决字符串匹配问题还有一种算法,那就是BF算法,也就是暴力破解法,但是BF算法比较耗时间,每一次不匹配时都,母串要回溯到开始匹配时的下一个位置,字串要回溯到开始位置,最坏的时间复杂度是O(n·m)。但是,有一些字符串是有一定规律的,就比如下面这个字符串一样:
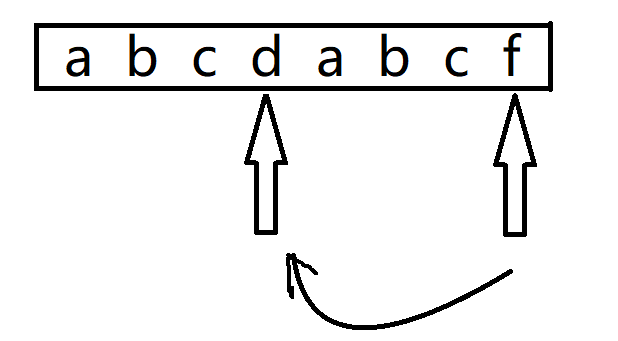
当在f这个字符不匹配时,我们会发现,我们可以直接将字串的指针直接移到d的位置,为什么呢?因为f的前面有abc,而刚好d前面也有abc,这表明,在母串上面,已经有一串abc和字串匹配过了,那么,我子串就没有必要在把前面那一截abc在比较一次了。这样子就减少了比较的次数了,从而达到优化的效果。kmp算法就是实现,当当前字符不匹配时,我的指针直接跳到像上面f->d的效果,从而实现优化。
所以,KMP算法适用于解决那些前后都有相同字段的字符串的匹配问题。
按照上面的思路,字符串T[0] ~ T[k-1]=T[j-k-1] ~ T[j-1],这时,我们把T[0] ~ T[k-1]叫作j的前缀,T[j-k-1] ~ T[j-1]叫作j的后缀。也就是说,kmp算法适用于有前缀和后缀的字符串的。
如果T[j]和母串不匹配时,我们要执行的操作是:j=k,也就是j的前缀的下一位,现在,我们做一个这样的数组next,就用来存放当T[j]不匹配时j要走的下一个位置。
然后,我们的问题就转化为了怎么求next数组,也就是说,如果在T[0] ~ T[j-1]的字符中,有T[0] ~ T[k-1]=T[j-k-1] ~ T[j-1]的,那我们就把k存放到next[j]中,这样子当j不匹配时,我们就可以直接跳到k的位置了。那么现在问题就转化为求next数组了。
求next数组
我们用两个指针k和j对模式串进行遍历,如果,k和j所指的内容相等,我们就把指针都前移,那么这时候,k的大小(+1之后才是)就表示着当前j指针前的字符串的前缀的长度,也就是当j不匹配时,j将要走的位置。上面这句话在代码中实现如下:
if(sub[k]==sub[j])
{
j++,k++;
Next[j]=k;
}
那如果k和j所指的的容不相等呢?此时分为以下两种情况:
- k=0,此时,j只能往前走
- k≠0,此时,k已经往前走了,但是现在不匹配了,也就是说,当前j的前缀已经达到最大,不会再增大了,对于往后的字符,就会有新的前后缀了。那么此时k是不是要从头开始呢,如果k前的字符串没有前后缀的话,确实是这样的。如果有的话,事实上我们把k移到Next[k]就好了。这个过程和子串和母串匹配的过程是一样的。下面给个例子:
![image]()
k和j不匹配了,那么j的前缀长度(即k的大小+1)又要从小变大了,也就是k要回退。这时,发现k的前缀:agc 和j前面的agc相同,那么我们把k移到T[3]的位置,即相当于前面的acg已经匹配了。在看,上述情况中,Next[k]=3,这不就巧了吗!事实上这不是巧合,这个就是像子串和母串不匹配时的情况是一样的。下面给出以上两种情况的代码:
if(k>0&&sub[k]!=sub[j]
{
k=Next[k];
}
else if(k==0)
{
j++;
}
所以,Next数组就算求完了。给出完整代码:
int Next[100] = {0};
void getNext(string sub)
{
int k = 0;
int j = 1;
int slen = sub.length();
while (j < slen)
{
if (sub[k] == sub[j])
{
j++, k++;
Next[j] = k;
}
else if (k > 0 && sub[k] != sub[j])
{
k = Next[k];
}
else if (k == 0)
{
j++;
}
}
}
Next数组优化
事实上,上面的的情况时可以优化的。
我们把k=0和k>0时匹配的情况整合起来可以这么做:我们把k的起始值设为-1,然后把Next[0]=-1;先上代码:
int Next[100] = {0};
void getNext(string str) {
int k = -1;
int j = 0;
Next[0] = -1;
int len = str.length();
while (j < len) {
if (k == -1 || str[k] == str[j]) {
k++;
j++;
Next[j] = k;
} else {
k = Next[k];
}
}
}
为什么可以这样?
我们可以发现,k=0时不匹配以及k!=0时匹配,j都要向前进的。
我们把k=-1,Next[0]=-1。刚开始是,k=-1,两个往前走,k=0;j=1;
这样子我们就把k=0的情况整合到k,j匹配的情况一同进行了,从而简化代码。
kmp算法实现
kmp算法最重要的就是求Next数组了,Next数组搞定了,kmp也就实现了,这里直接给代码了。
#include <bits/stdc++.h>
using namespace std;
int Next[100] = {0};
void getNext(string str) {
int k = -1;
int j = 0;
Next[0] = -1;
int len = str.length();
while (j < len) {
if (k == -1 || str[k] == str[j]) {
k++;
j++;
Next[j] = k;
} else {
k = Next[k];
}
}
}
int kmp(string momstr, string substr) {
int mlen = momstr.length();
int slen = substr.length();
int i = 0, j = 0;
getNext(substr);
while (i < mlen && j < slen) {
if (j == -1 || momstr[i] == substr[j]) {
i++, j++;
} else {
j = Next[j];
}
}
if (j == slen)
return i - j + 1;
else
return -1;
}
int main() {
string momstr, substr;
cin >> momstr >> substr;
cout << kmp(momstr, substr);
return 0;
}
到此为止,kmp算法就算讲完了。以上内容仅仅是个人的理解,若有什么不妥当的地方恳请大佬指正!

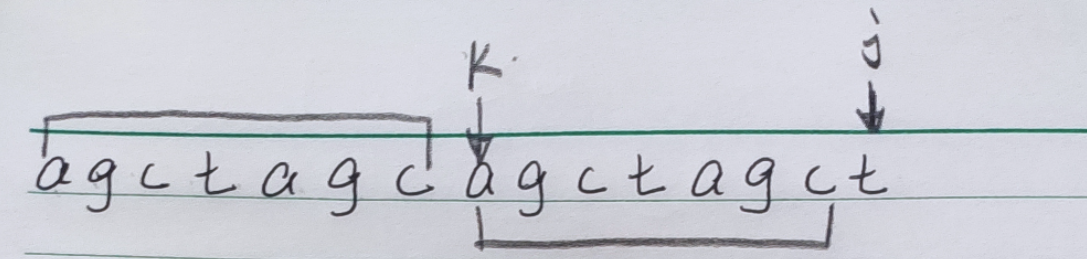

 浙公网安备 33010602011771号
浙公网安备 33010602011771号