Splay入门(平衡树)
一定要放在最前面的:
\(Splay\) 一个支持功能和 \(Treap\) 差不多的东西,只是更高级(有六种旋转操作)
既然是一种平衡树,那就具有 \(BST\) 性质
\(Update\)
void update(int p){
tr[p].size=tr[tr[p].son[0]].size+tr[tr[p].son[1]].size+tr[p].cnt;
//更新子树大小用于查询排名 ↑
}
\(Rotate\)
基本旋转操作
\(Treap\) 左旋和右旋操作的合并操作:
-
X变到原来Y的位置
-
Y变成了 X原来在Y的 相对的那个儿子
-
Y的非X的儿子不变 X的 X原来在Y的 那个儿子不变
-
X的 X原来在Y的 相对的 那个儿子 变成了 Y原来是X的那个儿子
void rotate(int x){
int y=tr[x].fa,z=tr[y].fa,k=(tr[y].son[1]==x);
//y是x的父亲,z是爷爷
//k用于判断x是y的左儿子还是右儿子;0:左,1:右
tr[z].son[tr[z].son[1]==y]=x;
tr[x].fa=z;
//x顶替y的位置 ↑
tr[y].son[k]=tr[x].son[k^1];
tr[tr[x].son[k^1]].fa=y;
//改变x的另一个儿子 ↑
tr[x].son[k^1]=y;
tr[y].fa=x;
//更改x,y的关系 ↑
update(y),update(x);//记得修改
}
\(Spaly\)
比 \(Treap\) 多出的旋转操作
单纯对 \(X\) 旋转两次后仍然有一条链的存在,还是可能会被卡
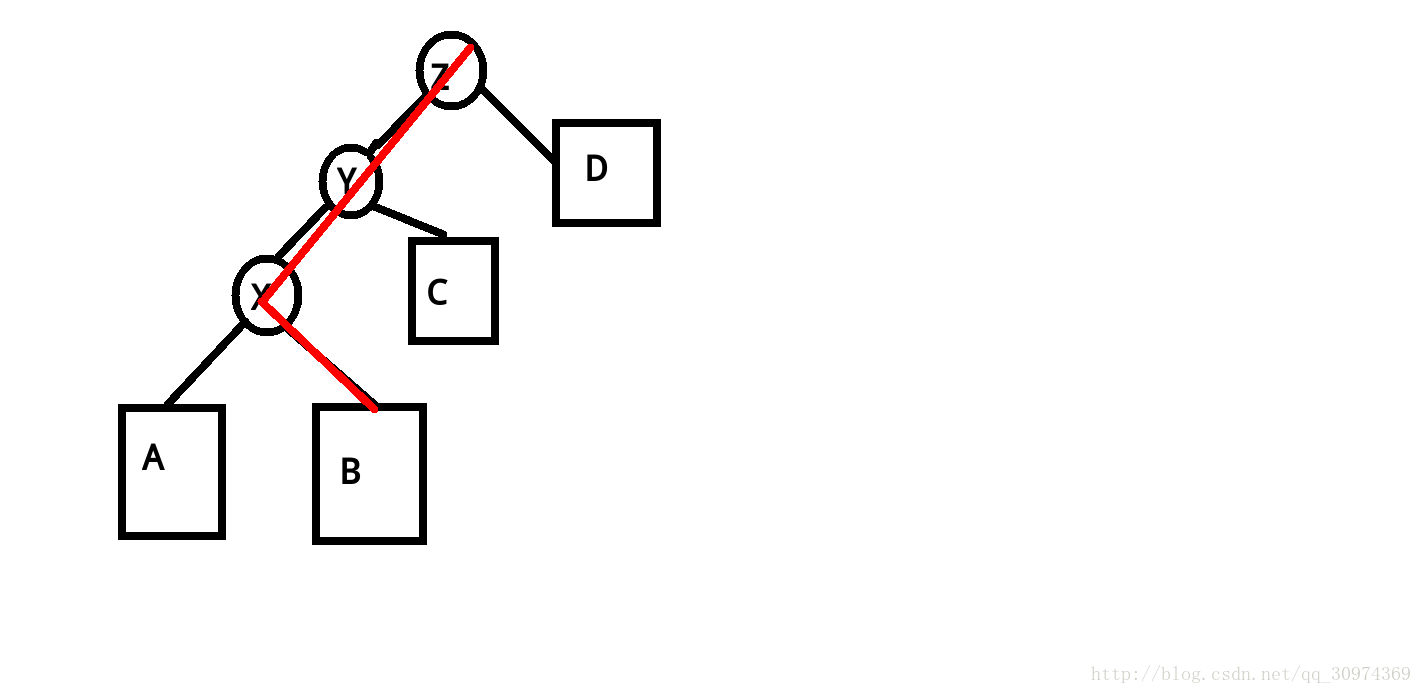
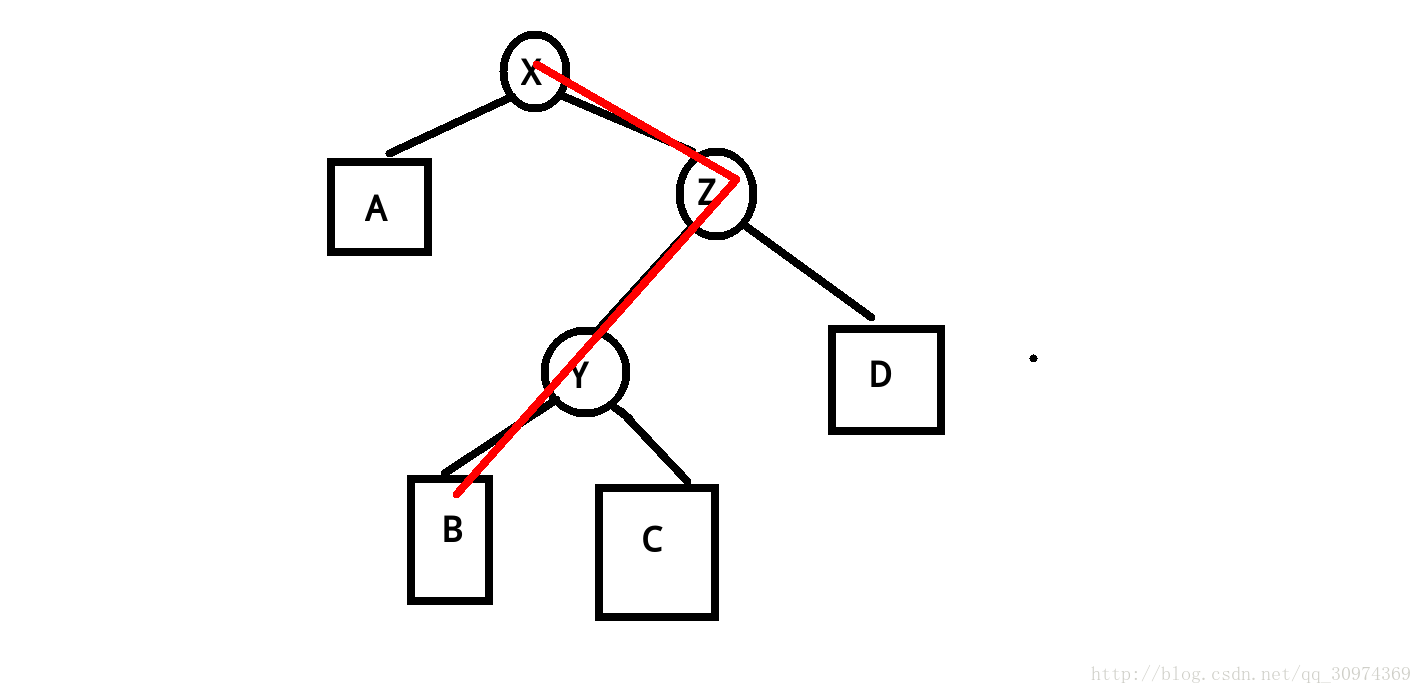
所以才有了 \(Splay\) 操作
两种情况:
-
X和Y分别是Y和Z的同一个儿子
-
X和Y分别是Y和Z不同的儿子
第一种情况:先转Y再转X
第二种情况:转两次X
另外两种情况:
不存在Z,即Y是树的根,只需要对X进行一次旋转即可
void splay(int x,int goal){//将x转为goal的儿子
while(tr[x].fa!=goal){
int y=tr[x].fa,z=tr[y].fa;
if(z!=goal)//y已经是目标节点的儿子,只需要转一次
((tr[z].son[0]==y)^(tr[y].son[0]==x))?rotate(x):rotate(y);
//在同一侧转y,否则转x
rotate(x);//最后转的都是x
}
if(goal==0) root=x;//0是根的父亲,记得换根
}
\(Find\)
查找后根就是要找的节点
void fi(int x){
int u=root;
if(!u) return;//树为空
while(tr[u].son[x>tr[u].val] && x!=tr[u].val)
u=tr[u].son[x>tr[u].val];//进入相应节点
splay(u,0);//此时u为查找值的编号,并旋转到根
}
\(Insert\)
和 \(Treap\) 的差不多
void insert(int x){
int fa=0,u=root;//fa是要插入节点的父节点
while(u && x!=tr[u].val){
fa=u;
u=tr[u].son[x>tr[u].val];
}
if(u) tr[u].cnt++;//存在直接累加值就好了
else{
u=++tot;
if(fa) tr[fa].son[x>tr[fa].val]=u;
tr[u].son[1]=tr[u].son[0]=0;
tr[u].fa=fa,tr[u].val=x,tr[u].cnt=1,tr[u].size=1;
}
splay(u,0);
//一定要转到根保证平衡。前面改了子树大小所以借此update
}
前驱&后继
int nxt(int x,bool k){//1为后继,0为前驱
fi(x);
int u=root;
if(tr[u].val>x && k) return u;
if(tr[u].val<x && !k) return u;
u=tr[u].son[k];
while(tr[u].son[k^1]) u=tr[u].son[k^1];
return u;
}
\(Remove\)
void remove(int x){
int la=nxt(x,0),nex=nxt(x,1);
splay(la,0),splay(nex,la);
//将前驱旋转到根节点,后继旋转到根节点下面
int del=tr[nex].son[0];
if(tr[del].cnt>1){
tr[del].cnt--;
splay(del,0);//修改子树大小
}
else tr[nex].son[0]=0;//直接删
}
找第 \(k\) 大
比较重要,还是附个代码吧
int kth(int x){//查第k大
int u=root;
if(tr[u].size<x) return 0;
while(1){
int y=tr[u].son[0];
if(x>tr[y].size+tr[u].cnt){
x-=tr[y].size+tr[u].cnt;
u=tr[u].son[1];
}
else{
if(tr[y].size>=x) u=y;
else return u;
}
}
}
完整代码
#include<bits/stdc++.h>
using namespace std;
#define INF 20000000
const int N=1e5+5;
struct splay_tree{
int fa,son[2],cnt,val,size;
}tr[N];
int root,tot;
inline void update(int p){
tr[p].size=tr[tr[p].son[0]].size+tr[tr[p].son[1]].size+tr[p].cnt;
}
inline void rotate(int x){
int y=tr[x].fa,z=tr[y].fa,k=(tr[y].son[1]==x);
tr[z].son[tr[z].son[1]==y]=x;
tr[x].fa=z;
tr[y].son[k]=tr[x].son[k^1];
tr[tr[x].son[k^1]].fa=y;
tr[x].son[k^1]=y;
tr[y].fa=x;
update(y),update(x);
}
inline void splay(int x,int goal){
while(tr[x].fa!=goal){
int y=tr[x].fa,z=tr[y].fa;
if(z!=goal)
((tr[z].son[0]==y)^(tr[y].son[0]==x))?rotate(x):rotate(y);
rotate(x);
}
if(goal==0) root=x;
}
inline void fi(int x){
int u=root;
if(!u) return;
while(tr[u].son[x>tr[u].val] && x!=tr[u].val)
u=tr[u].son[x>tr[u].val];
splay(u,0);
}
inline void insert(int x){
int fa=0,u=root;
while(u && x!=tr[u].val){
fa=u;
u=tr[u].son[x>tr[u].val];
}
if(u) tr[u].cnt++;
else{
u=++tot;
if(fa) tr[fa].son[x>tr[fa].val]=u;
tr[u].son[1]=tr[u].son[0]=0;
tr[u].fa=fa,tr[u].val=x,tr[u].cnt=1,tr[u].size=1;
}
splay(u,0);
}
inline int nxt(int x,bool k){
fi(x);
int u=root;
if(tr[u].val>x && k) return u;
if(tr[u].val<x && !k) return u;
u=tr[u].son[k];
while(tr[u].son[k^1]) u=tr[u].son[k^1];
return u;
}
inline void remove(int x){
int la=nxt(x,0),nex=nxt(x,1);
splay(la,0),splay(nex,la);
int del=tr[nex].son[0];
if(tr[del].cnt>1){
tr[del].cnt--;
splay(del,0);
}
else tr[nex].son[0]=0;
}
inline int rk(int p,int x){
if(!p) return 0;
if(x==tr[p].val)
return tr[tr[p].son[0]].size+1;
if(x>tr[p].val)
return rk(tr[p].son[1],x)+tr[tr[p].son[0]].size+tr[p].cnt;
return rk(tr[p].son[0],x);
}
inline int kth(int x){
int u=root;
if(tr[u].size<x) return 0;
while(1){
int y=tr[u].son[0];
if(x>tr[y].size+tr[u].cnt){
x-=tr[y].size+tr[u].cnt;
u=tr[u].son[1];
}
else{
if(tr[y].size>=x) u=y;
else return u;
}
}
}
int main(){
int n;
cin>>n;
insert(-INF),insert(INF);
while(n--){
int opt,x;
scanf("%d%d",&opt,&x);
if(opt==1) insert(x);
if(opt==2) remove(x);
if(opt==3) cout<<rk(root,x)-1<<endl;
if(opt==4) cout<<tr[kth(x+1)].val<<endl;
if(opt==5) cout<<tr[nxt(x,0)].val<<endl;
if(opt==6) cout<<tr[nxt(x,1)].val<<endl;
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号