jzoj5462

题意求长度为n的字符串中的长度为m的连续子串有多少个是不同的。

比如n=5， s=aaaab

它长度为3的子串有

aaa、aaa、aab

有两个不同的子串，答案为2。

解法有两种，其一是hash，其二是后缀自动机。

这里讲讲hash。

我用的双hash。

大意就是第一个hash用来查询，第二个hash用来判第一个hash的冲突（冲突的概率极小）

hash的写法：

预处理：

h1[0] = h2[0] = 0;
    for (int i = 1; i <= len; i++)
    {
        h1[i] = (h1[i - 1] * 131 + s[i]) % m1;
        h2[i] = (h2[i - 1] * 97 + s[i]) % m2;
    } 

求出每个子串的hash值：

for (LL i = 1; i <= len - m + 1; i++)
    {
        LL k1 = ((h1[i + m -1] - h1[i - 1] * ksm(131, m, m1)) % m1 + m1) % m1;
        LL k2 = ((h2[i + m -1] - h2[i - 1] * ksm(97, m, m2)) % m2 + m2) % m2;
        hash(k1, k2);
    }

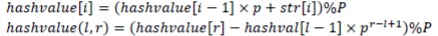
如上图所示

最后统计答案：

void add(LL k1, LL k2)
{
    a[tot].x = k2;
    a[tot].next = h[k1];
    h[k1] = tot++;
}

void hash(LL k1, LL k2)
{
    for (LL i = h[k1]; ~i; i = a[i].next)
        if (a[i].x == k2)
            return;
    add(k1, k2);
    ans++;
}

如果发现两个hash值都不同，则说明是一个新的子串。

完整代码：

#include <cstdio>
#include <cstring>
#define LL long long
using namespace std;

const LL maxn = 200005, m1 = 999973, m2 = 1000000000 + 9;

LL n, m, ans, tot;

LL h[m1 + 5], h1[maxn], h2[maxn];

char s[maxn];

struct node
{
    LL x, next;
}a[maxn];

void add(LL k1, LL k2)
{
    a[tot].x = k2;
    a[tot].next = h[k1];
    h[k1] = tot++;
}

void hash(LL k1, LL k2)
{
    for (LL i = h[k1]; ~i; i = a[i].next)
        if (a[i].x == k2)
            return;
    add(k1, k2);
    ans++;
}

LL ksm(LL a, LL b, LL mo)
{
    LL ans = 1, base = a;
    while (b)
    {
        if (b & 1)
            ans = (ans * base) % mo;
        base = (base * base) % mo;
        b >>= 1;
    }
    return ans % mo;
}

int main()
{
    freopen("article.in","r",stdin);
    freopen("article.out","w",stdout);
    ans = tot = 0;
    memset(h, -1, sizeof h);
    scanf("%lld%lld", &n, &m);
    scanf("%s", s + 1);
    LL len = strlen(s + 1);
    h1[0] = h2[0] = 0;
    for (int i = 1; i <= len; i++)
    {
        h1[i] = (h1[i - 1] * 131 + s[i]) % m1;
        h2[i] = (h2[i - 1] * 97 + s[i]) % m2;
    } 
    for (LL i = 1; i <= len - m + 1; i++)
    {
        LL k1 = ((h1[i + m -1] - h1[i - 1] * ksm(131, m, m1)) % m1 + m1) % m1;
        LL k2 = ((h2[i + m -1] - h2[i - 1] * ksm(97, m, m2)) % m2 + m2) % m2;
        hash(k1, k2);
    }
    printf("%lld\n", ans);
    return 0;
}

 P.S.：

这题我使用的是哈希表的方法，要求m1一定要比较小，m2不能取太大，否则后来的运算中可能会出现溢出的情况。

我一般取m1=999973，m2=1e9+9

这里还有另外一种方法。

我们把每次hash得到的两个数k1，k2，搞成一个pair。

然后把pair塞进一个vector中，排序并去重之，如此可以直接得到答案。

核心代码：

h1[0] = h2[0] = 0;
    for (int i = 1; i <= len; i++)
    {
        h1[i] = (h1[i - 1] * 131 + s[i]) % m1;
        h2[i] = (h2[i - 1] * 97 + s[i]) % m2;
    } 
    for (LL i = 1; i <= len - m + 1; i++)
    {
        LL k1 = ((h1[i + m -1] - h1[i - 1] * ksm(131, m, m1)) % m1 + m1) % m1;
        LL k2 = ((h2[i + m -1] - h2[i - 1] * ksm(97, m, m2)) % m2 + m2) % m2;
        v.push_back(make_pair(k1, k2));
    }
    sort(v.begin(), v.end());
    ans = unique(v.begin(), v.end()) - v.begin();
    printf("%lld\n", ans);

 PSS：

之前写的hash方法太慢，现在使用新的hash方法，大大提高了速度。（from O(nm) to O(n)）