2024“钉耙编程”中国大学生算法设计超级联赛(1)1012并
题目大意 :给出n个矩形,求被k个矩形覆盖的面积的并集的期望,输出k为1-n的所一答案
思路 :由于是求期望所以是求出所有情况的和再除以可能的情况,每一种情况中的面积都由--同时被1个矩形覆盖,同时被两个矩形覆盖······同时被k个矩形覆盖组成,而且不难得出当k一定时,取被m个矩形覆盖的面积次数是一定的,如图:
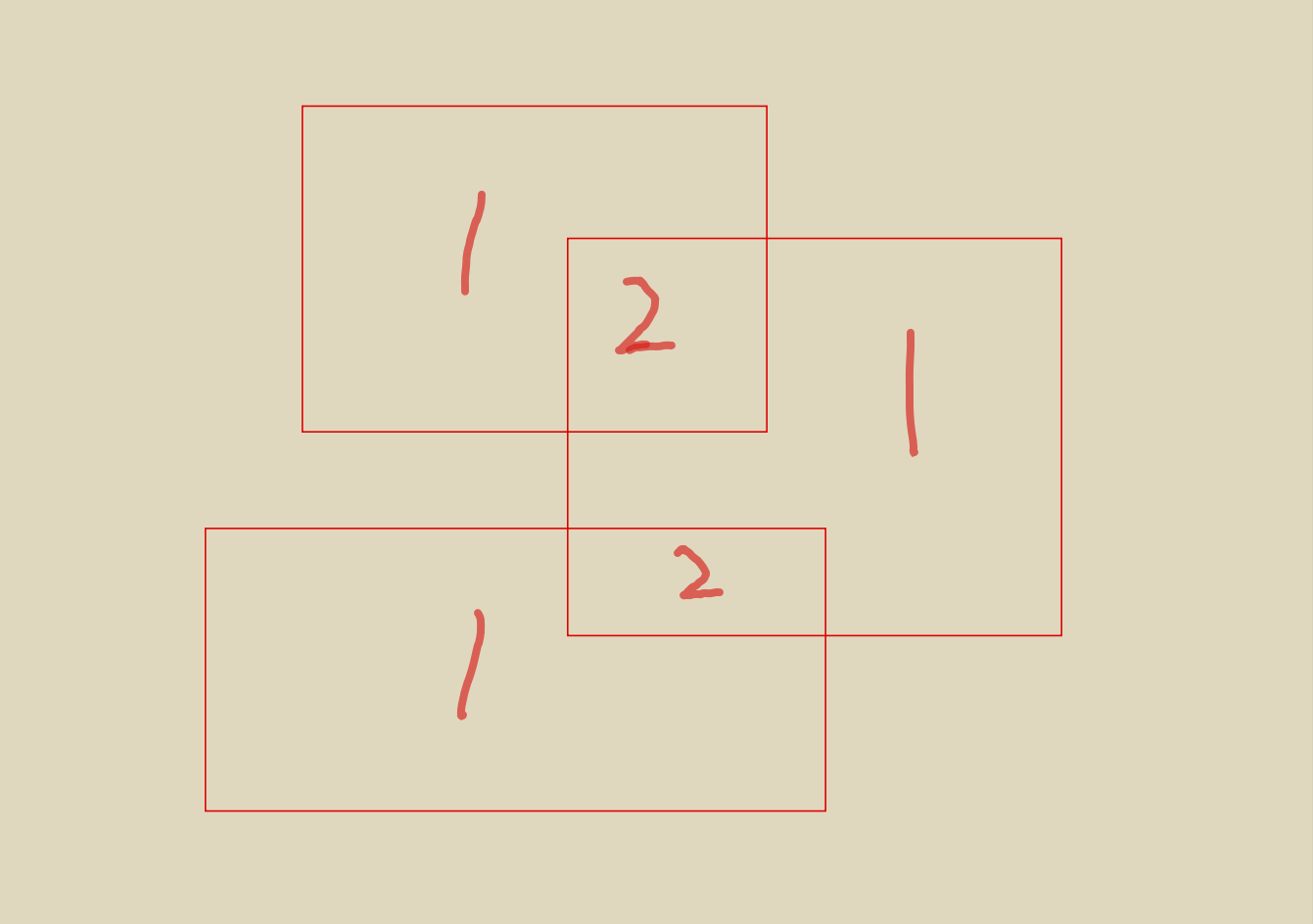
当k为1时 所有的1取均1次,所有的2取均2次
当k为2时 所有的1取均2次,所有的2取均3次
当k为3时 所有的1取均1次,所有的2取均1次
所以现在只需要求出被i个矩形覆盖的面积即可,那么可以通过离散化加拆分在O(\(n^2\))的时间复杂度下进行,最后被k个矩形覆盖的面积就是\(\sum_1^ng(i)\) ,取到这个被覆盖的面积的概率即为总概率减去取不到的概率\(1-\frac{C_{n-i}^k}{C_n^k}\) 即总期望为: \(\sum_1^n(1-\frac{C_{n-i}^k}{C_n^k})g(i)\)
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int MOD = 998244353;
#define all(x) x.begin(),x.end()
const int N = 4e3 + 10;
void mod(int &x, int a) { if ((x += a) >= MOD) x -= MOD; }
//----------------------------------//头文件和定义
struct rectangle {
int x1, y1, x2, y2;
};
int n;
vector<rectangle> rec(N);
vector<vector<int>> mp(N, vector<int>(N));
vector<int> rx, ry;
vector<int> fac(N + 1), invf(N + 1), g(N);
//------------------------------------//变量创建
void E(vector<int> &a) {
a.erase(unique(all(a)), a.end());
}
void presum(int x1, int x2, int y1, int y2) {
mp[x1][y1]++;
mp[x1][y2]--;
mp[x2][y1]--;
mp[x2][y2]++;
//cout << x1 <<' '<<x2 <<' '<<y1 <<' '<<y2 <<"\n";
}
int findidx(vector<int> a, int num) {
return lower_bound(all(a), num) - a.begin();
}
int qpw(int a, int b) {
int res = 1;
while (b) {
if (b & 1) res = res * a % MOD;
b >>= 1;
a = a * a % MOD;
}
return res;
}
void init() {
fac[0] = fac[1] = invf[0] = invf[1] = 1;
for (int i = 2; i < N; ++i) fac[i] = fac[i - 1] * i % MOD;
invf[N - 1] = qpw(fac[N - 1], MOD - 2);
for (int i = N - 1; i > 2; --i) invf[i - 1] = invf[i] * i % MOD;
}
//------------------------------------------//建立函数
void solve() {
cin >> n;
init();
for (int i = 0; i < n; i++) {
int x1, y1, x2, y2;
cin >> x1 >> y1 >> x2 >> y2;
rec[i] = {x1, y1, x2, y2};
rx.emplace_back(x1);
rx.emplace_back(x2);
ry.emplace_back(y1);
ry.emplace_back(y2);
}
rx.emplace_back(-2e9);
ry.emplace_back(-2e9);
sort(all(rx));
E(rx);
sort(all(ry));
E(ry);
for (int i = 0; i < n; i++) {
int x1 = findidx(rx, rec[i].x1);
int x2 = findidx(rx, rec[i].x2);
int y1 = findidx(ry, rec[i].y1);
int y2 = findidx(ry, rec[i].y2);
presum(x1, x2, y1, y2);
}
int lrx = rx.size();
int lry = ry.size();
for (int i = 1; i < lrx; i++) {
for (int j = 1; j < lry; j++) {
mp[i][j] += mp[i][j - 1];
}
}
for (int i = 1; i < lrx; i++) {
for (int j = 1; j < lry; j++) {
mp[i][j] += mp[i - 1][j];
//cout <<i<<' '<<j<<" "<< mp[i][j]<<'\n';
g[mp[i][j]] = (g[mp[i][j]] + (rx[i + 1] - rx[i]) * (ry[j + 1] - ry[j]) % MOD) % MOD;
}
}
for (int k = 1; k <= n; ++k) {
int ans = 0;
for (int t = 1; t <= n; ++t) {
if (n - t - k >= 0)
ans = (ans + g[t] * (MOD + 1 -
fac[n - t] * invf[n - t - k] % MOD * fac[n - k] % MOD * invf[n] %
MOD) % MOD) % MOD;
else ans = (ans + g[t]) % MOD;
}
cout << ans << '\n';
}
}
signed main() {
ios::sync_with_stdio(false), cin.tie(0), cout.tie(0);
int _ = 1;
//cin >> _;
while (_--) {
solve();
}
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号