详细实验指导见上上一篇,此处只写内容啦
实验内容
选择 y=arctan(x) 在0-1上的积分
准确积分结果:
精确值(保留二十位有效数字)为

程序实现
• 复化梯形算法
function Tn=Tn(a,b,n)
syms x
h=(b-a)/n;
sum=0;
f(x)=atan(x);
for k=1:n-1
sum=sum+f(a+k.*h);
end
Tn=(f(a)+2*sum+f(b))*h/2;
end
运行结果:

• 复化simpson公式
%%复化simpson法
syms x
a=0; %积分区间左端点
b=1; %积分区间右端点
n=50;
h=(b-a)/n;
f(x)=atan(x);
g(x)=a+x*h;
s1=0;
for i=0:n-1
s1=s1+f(g(i+1/2));
end
s2=0;
for j=1:n-1
s2=s2+f(g(j));
end
S=h/6*(f(a)+4*s1+2*s2+f(b));
fprintf('复化simpson法=%g\n',S);
运行结果:
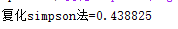
• 复化科特斯法
function Cn = Cn(a,b,n)
format long
syms x
f(x)=atan(x);
h = (b-a)/n;
sum1 = 0;
sum2 = 0;
for i = 0:n-1
sum1 = sum1 + 32*f(a+(i+1/4).*h)+12*f(a+(i+1/2).*h)+32*f(a+(i+3/4).*h);
end
for j = 1:n-1
sum2 = sum2 + 14*f(a+j.*h);
end
Cn = h/90*(7*f(a)+sum1+sum2+7*f(b));
运行结果:

• 另复化科特斯法
syms x
a=0; %积分区间左端点
b=1; %积分区间右端点
n=50;
h=(b-a)/n;
f(x)=atan(x);
g(x)=a+x*h;
c1=0;
for i=0:n-1
c1=c1+h/90*(7/n*f(a)+32*f(g(i+1/4))+12*f(g(i+1/2))+32*f(g(i+3/4))+14*f(g(i))+7/n*f(b));
end
C1=c1-h/90*14*f(g(0));
fprintf('复化柯特斯法=%g\n',C1);
运行结果:
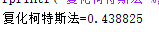
• 龙贝格公式
syms x
a=0; %积分区间左端点
b=1; %积分区间右端点
n=50;
h=(b-a)/n;
h1=(b-a)/(2*n);
f(x)=atan(x);
g(x)=a+x*h;
g1(x)=a+x*h1;
c1=0;
for i=0:n-1
c1=c1+h/90*(7/n*f(a)+32*f(g(i+1/4))+12*f(g(i+1/2))+32*f(g(i+3/4))+14*f(g(i))+7/n*f(b));
end
C1=c1-h/90*14*f(g(0));
c2=0;
for i=0:2*n-1
c2=c2+h1/90*(7/(2*n)*f(a)+32*f(g1(i+1/4))+12*f(g1(i+1/2))+32*f(g1(i+3/4))+14*f(g1(i))+7/(2*n)*f(b));
end
C2=c2-h1/90*14*f(g1(0));
Rn=64/63*C2-1/63*C1;
fprintf('龙贝格公式法=%g\n',Rn);
运行结果:
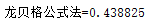

 posted on
posted on

 浙公网安备 33010602011771号
浙公网安备 33010602011771号