滑动窗口

leetcode算法题：长度最小的子数组

题目链接

暴力解法

使用两个for循环，第一层循环移动数组的起始位置，第二层循环移动数组的终止位置，时间复杂度O(n^2)。

class Solution {
public:
    int minSubArrayLen(int target, vector<int>& nums) {
        int s;
        int result = INT_MAX;
        int subLength;
        for(int i = 0; i < nums.size(); i++) {
            s = 0;
            for(int j = i; j < nums.size(); j++) {
                s += nums[j];
                if(s >= target) {
                    subLength = j-i+1;
                    result = subLength<result ? subLength :result;  //s>=target后不能马上就返回subLength，要继续找到满足条件的最小长度
                }
            }
        }
        return result == INT_MAX ? 0 :result;  //如果都不符合条件，即result没有被赋值，则返回0
    }
};

 滑动窗口

    ——学自“代码随想录”

滑动窗口，就是不断的调节子序列的起始位置和终止位置，从而得出我们要想的结果。

暴力解法实际上也是滑动窗口的一种，现在想办法看是否能在一个for循环中进行窗口的滑动。

1、如果一次循环中，固定起始位置，移动终止位置，则与暴力解法类似

2、如果一次循环中，固定终止位置，移动起始位置：
     1）s<target，后移终止位置
     2)  s>=target，后移起始位置

将2翻译为代码：

int i=0;  //i指向起始位置，j指向终止位置
for(int j=0; j<nums.size(); j++) {
    s += nums[j];
    while(s >= target) {
        subLength = j-i+1;
        result = subLength < result ? subLength : result;
        s -= nums[i++];   //不是只i++,而是把num[i]移除s中
    }
}

 

---

 

相关题目

1、水果成篮

题目链接

剖解题意：连续采摘，最大区间

代码：

class Solution {
public:
    int totalFruit(vector<int>& fruits) {
        int i = 0; //起始位置
    int subLength; //每一次的采摘水果量
    int total = INT_MIN; //最大的采摘水果量
        int first = -1,second = -1; //记录水果的第一种和第二种种类 
    int j; //终止位置 
        for(j = 0; j < fruits.size(); j++) {
            if(first == -1) {
                first = fruits[j];  
            }
            if(fruits[j] != first && fruits[j] != second) {  //出现第三种水果，此次采摘结束，重新定义采摘起始点
                if(second == -1) {
                    second = fruits[j];
                continue;
            } 
            subLength = j-i;  //记录当前采摘水果量 
            total = total < subLength ? subLength : total;  //更新total，使total保持为最大结果
            i = j-1;    
            while(fruits[i] == fruits[i-1]) {
                i--;
            }                  //从后往前查找新的采摘起始点，使现在的采摘区间中只有两种水果
            first = fruits[i];
            second = fruits[j];  //重新记录两种水果
        } 
    } 
    subLength = j-i;
    total = total < subLength ? subLength : total;    //退出循环后，还需要记录最后一次的结果
    return total;
    }
};

代码的优化：

——思路来源于LeetCode “Link”

1、上述的代码在出现第三个水果后，i从j-1开始寻找下一次采摘的初始位置，可以用一个变量存储这个位置，省去每次查找的过程

2、退出循环后的代码使可读性下降

class Solution {
public:
    int totalFruit(vector<int>& fruits) {
        int i = 0,j; //起始位置和终止位置 
        int subLength; 
        int total = INT_MIN;
        int first = 0,second = 0; //第一种水果和第二种水果的起始索引 
        int t = 0;  //下一次的第一个篮子的水果的起始索引 
        for(j = 0; j < fruits.size(); j++) {
            if(fruits[j] != fruits[first] && fruits[j] != fruits[second]) {
                if(first != second) {  //出现第三种水果 
                    first = t; 
                 }
                 second = j;
            }
            if(fruits[t] != fruits[j]) {
                t = j;
            }
            subLength = j-first+1;
            total = total < subLength ? subLength : total;     
    } 
    return total;
    }
};

 

 2、最小覆盖子串

题目链接

首先，强调在做题中很重要的一点：记得初始化变量，在做这道题时因为int类型的变量没有初始化0，在函数就对其进行++运算，导致出错。

1、确定了用滑动窗口的思想

2、如何确定窗口内包含t所有的字符——使用两个哈希表，一个哈希表存t中字母出现的次数，另一个哈希表存现已找到的字母的个数。

借用力扣官方的一张图，清楚地描述了窗口滑动的过程，转换为代码即可。

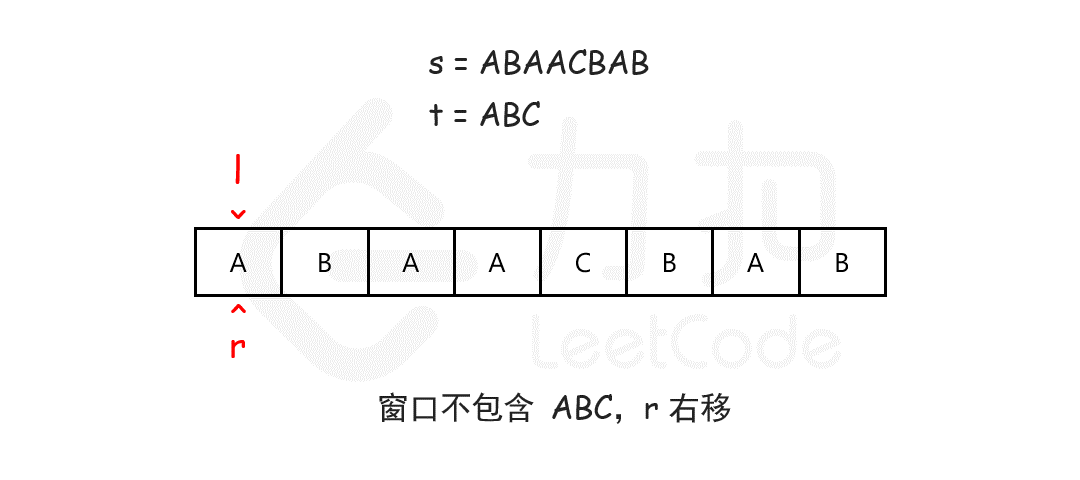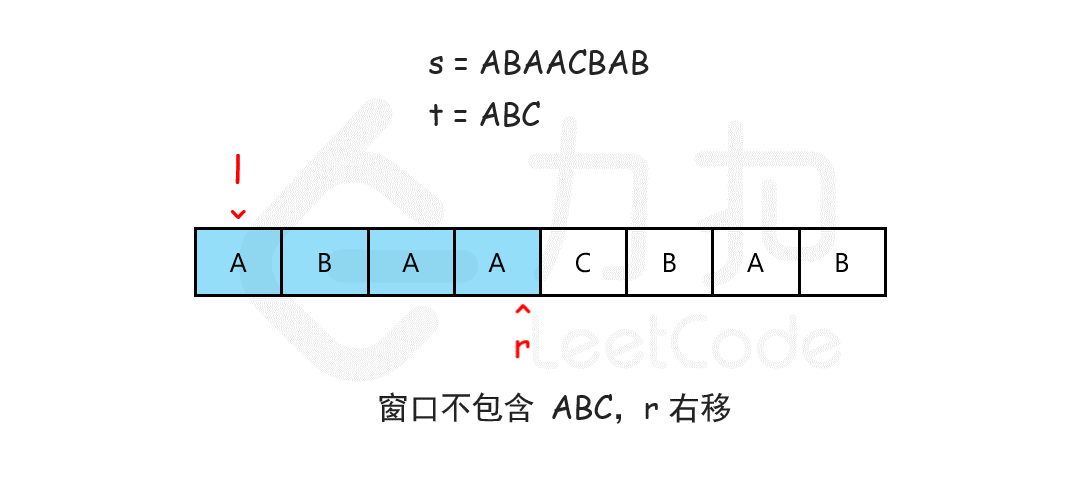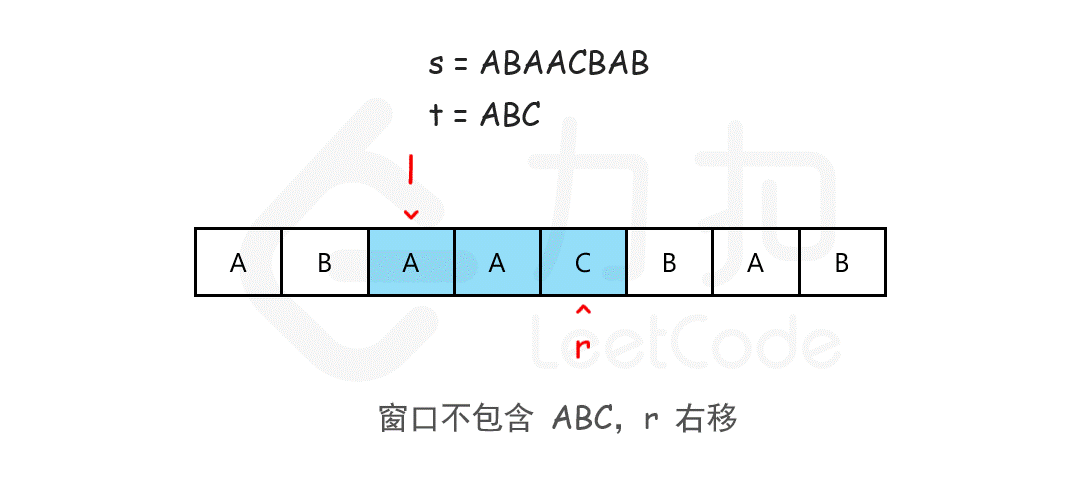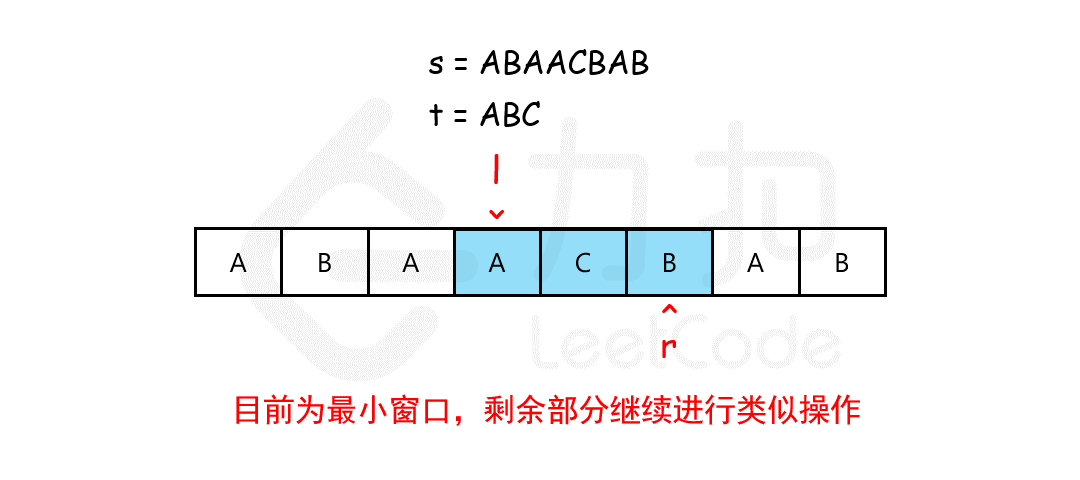
代码：

class Solution {
    public:
        map<char,int>ori,cnt; //ori是t中字母出现的次数，cnt是已找到字母的个数 
        bool check() {     
            for(const auto&p : ori) {
                if(cnt[p.first] < p.second) {  
                    return false;
                }
            }
            return true;
        }
        string minWindow(string s, string t) {
            int i = 0,j = -1; //标记起始位置和终止位置 
            int len = INT_MAX;
            string object;
            for(const auto &c:t) {
                ori[c]++;
            }
            while(j < (int)s.length()) {
                if(ori.find(s[++j]) != ori.end()) {   //若j初始值为0，此处写为j++，则在进行cnt[s[j]]++;时，j已经改变，出错 
                    cnt[s[j]]++;
                }
                while(check() && i <= j) {
                    if(j-i+1 < len) {
                        len = j-i+1;
                        object = s.substr(i,len);
                    }
                    //缩小窗口 
                    if(ori.find(s[i]) != ori.end()) {
                        cnt[s[i]]--;       //缩小窗口的同时要记得更新cnt 
                    }
                    i++;
                }
            }
            return len == INT_MAX ? "" : object;    
        }
};