CF2191

比赛链接

A

满足第一个条件的颜色序列至多 2 种，暴力判就行了。

B

结论：合法当且仅当要么只有一个 \(0\)，要么有至少两个 \(0\) 且至少有一个 \(1\)。

C

结论：至多只需要一次操作就能把局面变成 \(000\ldots111\) 的形式。如果需要一次操作，则 Alice 赢；否则 Bob 赢。

证明及构造：找到位置 \(p\) 满足 \([1, p]\) 中的 \(1\) 和 \((p, n]\) 中的 \(0\) 个数相等，可以证明 \(p\) 存在且唯一。把上述 \(1\) 和 \(0\) 做一次操作。

D1

考虑贪心，发现你需要把第一个 ) 变成 (，且后面要删掉任意 2 个 (。故答案为 \(n - 2\) 或 \(\texttt {-1}\)，用上述条件判一下。

D2

考虑 dp，沿用 D1 的方法，记 \(f _ {i, j, k}\) 表示考虑前 \(i\) 个括号，当前 ( 比 ) 多了 \(j\) 个，还剩 \(k\) 个 ( 括号没有删的方案数，类似地记 \(g _ {i, j, k}\) 表示 \(len - 2\) 的和，在第一个取 ) 的位置加入初值，转移和计算答案是容易的。

E

假设第一个 \(q _ i > p _ i\) 的位置为 \(pos\)，则 \(i\) 后面必须存在比 \(p _ i\) 更大的数。我们希望 \(pos\) 尽可能大。

具体分析一下，假设 \(pos\) 是一个合法的位置，我们的策略是把 \(p _ {pos}\) 和 \([pos + 1, n]\) 中 \(p _ {pos}\) 的值域上的后继交换后，再对 \([pos + 1, n]\) 从小到大排序。手动模拟一下情况，发现合法且最大的 \(pos\) 的条件有两个：

1. \(p _ {pos} < p _ {pos + 1}\)。
2. \(p _ {pos + 1}, p _ {pos + 2}, \ldots, p _ n\) 不能是递增的。

于是从后往前找就可以了。找的过程花费至多 \(n\) 次操作；排序可以归并，至多 \(n\) 次操作；找后继也至多 \(n\) 次操作。

F

删叶子的过程肯定是先把树删成 \(n\) 到 \(n - 1\) 的一条链，再从 \(n - 1\) 开始依次删掉，所以另外一个节点是从 \(n\) 到 \(n - 1\) 路径上第二个节点。

\(n\) 和 \(n - 1\) 在同一个连通块的情况是简单的，把它特判掉。剩下的我们分几种情况讨论：

1. \(n - 1\) 最终连到 \(n\) 所在连通块内的其他节点，而非 \(n\) 本身：因为 \(n\) 所在连通块内的每个点本质相同，所以对于与 \(n\) 相邻的每个节点 \(x\)，都有总方案数 \(\times \frac {siz _ x} {siz _ n}\) 的贡献。

2. 否则，若 \(n - 1\) 所在连通块直接连到 \(n\)：由于 \(n - 1\) 所在连通块内每个点本质相同，所以对于连通块内每个点 \(x\)，都有把 \(n - 1\) 所在连通块和 \(n\) 所在连通块合并后总方案数的贡献。

3. 否则：考虑其他连通块内的点 \(x\)，由于把 \(x\) 所在连通块和 \(n\) 所在连通块合并后，里面的每个点本质相同，故 \(n - 1\) 最终连到其中每个点的概率相等，所以对 \(x\) 有把 \(x\) 所在连通块和 \(n\) 所在连通块合并后总方案数 \(\times \frac {siz _ x} {siz _ x + siz _ n}\) 的贡献。

G

关键观察：\(f (p)\) 合法必为 \(2 \sim (n - 1)\) 的排列！

把奇数下标和偶数下标分开，发现一些子结构：

• \(p _ 1 < p _ 3 > p _ 5\) 合法当且仅当 \(p _ 3 = n\)。
• \(p _ 1 > p _ 3 < p _ 5\) 合法当且仅当 \(p _ 3 = 1\)。
• \(p _ 1 < p _ 3, p _ 2 > p _ 4\) 及其对称情况合法当且仅当 \(\max \{p _ 1, p _ 3\} < \min \{p _ 2, p _ 4\}\) 或 \(\min \{p _ 1, p _ 3\} > \max \{p _ 2, p _ 4\}\)。

于是我们这样刻画序列的大小关系形态（偷一下官方题解的好图）：

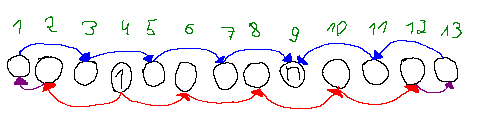
上文提到的 3 个子结构所限制的有效边分别用蓝色、红色、紫色表示。然后大小关系就变成了独立的两条链：

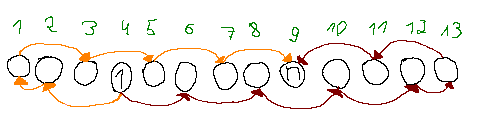
对于值 \(1\) 和 \(n\) 所在位置奇偶性相同的情况也同理：

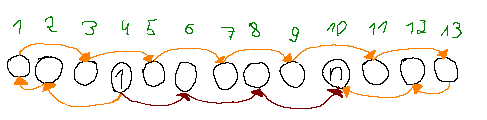
你先把这两条链找出来，考虑到有些 \(a _ i\) 初始被钦定了值，可以归并两条链、组合数计算解决。

归并时可能需要记录两个变量 \(l _ 1, l _ 2\) 表示两条链分别填了几个数，事实上 \(l _ 1, l _ 2\) 的取值不受你的决策影响。