< 算法笔记（晴神宝典) - 读书笔记 >（完结）

< 算法笔记（晴神宝典) - 读书笔记 >

< 算法笔记（晴神宝典) - 读书笔记 >

第二章：C++快速入门

2.5 数组

• memset - 对数组中每一个元素赋相同的值 - 用于初始化 / 重置

  • memset(数组名,值,sizeof(数组名));

  • 一般初始化 0 或者 -1 ，因为memset使用的是按字节赋值，这样int类型的4个字节都会被赋成相同的值。

  • 若要对数组赋为其他数字 - 使用STL中的fill函数

• string.h头文件函数

  • strlen(字符数组);

    • 得到字符数组中第一个\0前的字符个数

  • strcmp(字符数组1,字符数组2);

    • 返回两个字符串大小比较结果，比较原则是按字典序 - <返回负整数 =返回0 >返回正整数

  • strcpy(字符数组1,字符数组2)；

    • 把字符数组2复制给字符数组1 - 包括结束符\0

  • strcat(字符数组1,字符数组2)

    • 把字符数组2拼接到字符数组1后

• sscanf & sprintf

  • string + scanf / printf

2.7 指针

• 数组名作为函数参数，相当于指针传入，引用调用
  + * (a+i) == a[i]

  • q-p == &a[i] - &a[j] 相差距离

• 指针引用 - 引用别名

2.8 结构体

• 结构体内部可以定义自身的指针

• 结构体构造函数 - 初始化序列

• 结构体定义后直接申明的变量都是调用默认构造函数 - 跟C++构造函数一样的注意点

2.9 补充

• cin / cout 只有在string输出时才调用，一般多使用printf / scanf， 因为在输出大量数据时很容易超时

• 浮点数精度

const double eps = 1e-8;
const double Pi = acos(-1.0);

# define Equ(a,b) ((fabs((a)-(b)))<(eps))   // ==
# define More(a,b) (((a)-(b))>(eps))    // > 
# define Less(a,b) (((a)-(b))<(-eps))    // < 
# define More(a,b) (((a)-(b))>(-eps))    // >= 
# define More(a,b) (((a)-(b))<(eps))    // <= 

2.10 黑盒测试

while(scanf("%d %d",&a,&b) != EOF)
while(scanf("%s",str) != EOF)
while(gets(str) != NULL)

第四章 入门篇 - 算法初步

4.1 排序

4.1.1 选择排序

• n趟枚举选出依次最小元素

void selectSort(){
    for(int i = 1;i <= n; i++){ //进行n趟操作
        int k = i;
        for (int j =i; j <= n; j++){    //选出[i,n]中最小元素，下标为k
            if(A[j] < A[k])
                k = j;
        }
        int temp = A[i];
        A[i] = A[k];
        A[k] = temp;
    }
}

4.1.2 插入排序

• 序列分为有序与无序两部分，将无序部分一一插入有序部分合适位置处，进行n-1趟

int A[maxn], n;     //n为元素个数，数组下标为1-n
void insertSort(){
    for(int i = 2; i <= n; i++){    //进行n-1趟排序
        int temp = A[i], j = i;     //temp临时存放A[i]，j从i开始往前枚举
        while(j > 1 && temp < A[j-1]){  //只要temp小于前一个元素A[j-1]
            A[j] = A[j-1];      //则把A[j-1]后移一位
            j--;
        }
        A[j] = temp;
    }
}

4.1.3 排序题与sort函数应用

• 通常做题需要排序时直接调用C++的sort函数即可

  • C中的qsort涉及许多复杂指针操作

  • 规避了经典快排极端情况会出现O(n<sup>2</sup>)

• sort(首元素地址，尾元素地址的后一个地址 [，cmp比较函数] )

  • #include<algorithm>

  • using namespace std;

  • sort函数会原地修改传入序列

int a[6] = {5,6,4,1,3,2}
sort(a,a+4) //将a[0]~a[3]进行排序
sort(a,a+6) //将a[0]~a[5]进行排序

• 对非可比类型，比如类，结构体等，需要实现cmp比较函数

  • STL标准容器里vector，string，deque是可用sort的，而set，map本身有序（由红黑树实现不需排序）

  • 不填cmp参数，则默认对可比较类型进行从小到大排序

bool cmp(int a, int b){     // 实现int类型从大到小排序
    return a>b;     // 返回结果为True时，a在b前排序；否则b在a前排序
}

struct node {
    int x,y;
}ssd[10];

bool cmp(node a, node b){   //实现对结构体的排序
    return a.x > b.x    // True则ab，false则ba  - 一级排序
}
bool cmp(node a, node b){   // 二级排序
    if(a.x != b.x)  return a.x > b.x;   //x不等时按x从大到小排序
    else return a.y < b.y;  //x相等时按y从小到大排序
}

• 排序题sort应用与相关Tricks

  • 按string字典序大小排序：使用strcmp(s1,s2) - 返回值>0或<0

  • 并列排名，eg. 1、2、2、4：

    • 直接设置一个变量记录或定义结构体时将排名项加入结构体中；

    • 之后先排序，后修改结构体内的排名值：a[0]=1，遍历剩余元素，若分数等于上个元素分数，则排名值相同，否则等于下标+1

// strcmp(s1,s2)应用
bool cmp(student a, student b){
    if(a.score != b.score)  return a.score > b.score;
    else return strcmp(a.name, b.name) < 0;     //名字字典序小的在前
}

// 并列排名问题 1 - 需要存储
stu[0] = 1;     //有序数组
for(int i = 1; i<n; i++){
    if(stu[i].score == stu[i-1].score)
        stu[i].rank = stu[i-1].rank;
    else stu[i].rank = i + 1;
}

// 并列排名问题 2 - 直接输出
r = 1;
for(int i  = 0;i < n;i++){
    if(i>0 && stu[i].score != stu[i-1].score )
        r = i+1;
    //  输出信息 or stu[i].rank = r;
}

4.2 散列

4.2.1 散列定义与整数散列

• 常见散列函数：直接定址法（恒等变换&线性变换） 平方取中法 除留余数法（mod常为素数）

  • 哈希冲突：开放定址法（线性探查&平方探查） 拉链法

  • map（C++11中unordered_map）

4.2.2 字符串hash初步

• 非整数key映射整数value（初步暂时不讨论冲突，只讨论转化成唯一的整数）

  • 二维坐标点映射整数（0<x,y<R）- H(P) = x * R + y 唯一映射

• 字符串hash

  • 字符串由A~Z构成 - 将其看成26进制，转换成十进制整数映射：26^len-1 最大表示整数

  • 若有A_Zaz构成 - 则将其看成52进制，处理方法与上一致

  • 若出现数字，则有两种处理方法：

    • ① 与上一样，化为62进制

    • ② 若是只出现在特定位置，比如最后一位，则可以用拼接的方式：将前面的字母映射为十进制，拼接上后续数字

// A~Z
int hashFunc(char S[], int len){
    int id = 0;
    for(int i = 0; i < len; i++){
        id = id * 26 + (S[i]-'A')
    }
    return id;
}

// A~Za~z
int hashFunc(char S[], int len){
    int id = 0;
    for(int i = 0; i < len; i++){
        if(S[i]<='Z' && S[i]>='A')      // Z~a之间在ascll上不是相连的
            id = id * 52 + (S[i]-'A');
       else if(S[i]<='z' && S[i]>='a')
            id = id * 52 + (S[i]-'a') + 26;
    }
    return id;
}

// 假设A~Z且最后一位是数字
// A~Z
int hashFunc(char S[], int len){
    int id = 0;
    for(int i = 0; i < len; i++){
        id = id * 26 + (S[i]-'A');
    }
    id = id*10 + (S[i]-'0');
    return id;
}

4.3 递归

• 分治 & 递归

• 递归式 & 递归边界

4.4 贪心

• 简单贪心：当前局部最优来获得全局最优 - 贪心的证明思路一般使用反证+数学归纳法，证明比想到更难，若是想到时自己暂时也无法举出反例，则一般来说是正确的

• 区间贪心：

  • 区间不相交问题：给出N个开区间，选择尽可能多的开区间，使得两两之间没有重合。 - 贪心策略：先按左端点大小排序（右端点大小），总是选择最大左端点（最小右端点）

  • 区间最小点：给出N个开区间，选择最少的点，使得各区间都有点分布 - 与上述贪心策略相反，就是区间相交问题

  • 贪心解决最优化问题 - 思想希望由局部最优求解全局最优 - 适用问题需具有最优子结构性（即一个问题最优解能由其子结构最优解求得） - 贪心解决问题范围有局限性

#include <cstdio>
#include <algorithm>
using namespace std;
const int maxn = 110;
struck Inteval {
    int x,y;    // 开区间左右端点
} I[maxn];

bool cmp(Inteval a, Inteval b){
    if(a.x != b.x) return a.x > b.x;
    else return a.y < b.y;
}

int main(){
    int n;
    while(scanf("%d", &n), n != 0){
        for(int i = 0; i<n; i++)
            scanf("%d%d",&I[i].x, &I[i].y);
        sort(I, I+n ,cmp);  //区间端点排序
        
        //ans记录不相交区间个数，lastX几里路上一个被选中区间的左端点
        int ans = 1, lastX = I[0].x;
        for(int i =1; i<n; i++){
            if(I[i].y <= lastX){        //如果该区间右端点在lastX左边，表示没有重合
                lastX = I[i].x;     //以I[i]作为新选中区间
                ans++;  //不相交区间个数+1
            }
        }
        printf("%d\n",ans);
    }
    return 0;
}

4.5 二分

4.5.1 二分查找（整数二分）

• 基于有序序列查找算法，查找第一满足条件的位置，时间复杂度O(logⁿ)

  • mid = left+(right-left)/2（避免int越界），[left,mid-1]，[mid+1,right]；

  • 临界条件：1、查找到 2、left>right

  • 二分条件：1、循环left，相等时就是需要的值直接返回即可 2、二分初始区间为[0,n]

  • ①：序列中是否存在满足条件的元素 ②：寻找有序序列第一个满足某条件元素位置

// 序列中是否存在满足条件的元素 
int binarySearch(int A[], int left, int right, int x){
    int mid;    // mid为left和right中点
    while(left <= right){
        mid = left+ (right - left) / 2;
        if(A[mid] == x) return mid;
        else if(A[mid] > x)
            right = mid - 1;
        else left = mid + 1;
    }
    return -1;
}

// 寻找有序序列第一个满足某条件元素位置
int solve(int left, int right){     //左闭右闭写法
    int mid;
    while(left < right){        // 若左开右闭，则 left+1<right
        mid = left + (right - left)/2;
        if( 条件成立 ){
            right = mid;
        } else left = mid +1;       // 若左开右闭，则 left=mid
    }
    return left;    // 左开右闭，return right
}

4.5.2 二分法拓展

• ① 二分法 - 罗尔定理求方程根 eg.f(x)=x²-2=0 求在[left,right]范围方程根

• ② 二分答案：二分法查找结果

  • eg. 给N根木棒，切割希望得到至少K段长度相等的木棒，请问切割最长长度是多少。（切分长度越长，得到的段数越少 - 线性有序）

  • 相当于问：一个有序序列中，满足k>=K的最后一个元素位置 - 满足k<K的第一个元素位置(递减序列)，利用上述模板即可解决

4.5.3 快速幂

• 求幂朴素做法 O(n)：aⁿ=a * a * a..... 一共进行n次乘法

• 快速幂基于二分思想，亦称二分幂，即将幂部分/2拆分，如此只需要进行logⁿ次乘法 O(logⁿ)

  • 递归写法：n/2每次

    • if n = 奇数：aⁿ = a * aa^n-1

    • if n = 偶数：aⁿ = a^n/2 * a^n/2

    • 为了加快运算，奇偶判断使用位运算：if(n&1)

  • 迭代写法：将n化为二进制，二进制第i位上有数，化为a^2i-1

    • eg. a¹¹ = a²³ * a²¹ * a²⁰

    • 步骤①：n&1判断二进制末尾是否=1，ans是则乘以a

    • 步骤②：a=a²，n>>=1，只要n大于0，则继续步骤①；结果ans返回

// 快速幂递归写法
typedef long long LL;
LL binaryPow(LL a, LL b){
    if(b == 0) return 1;
    if(b & 1) return a * binaryPow(a,b-1);
    else{
        LL mul = binaryPow(a,b/2)     // 不能同时调用两个binaryPow，时间复杂度指数倍
        return mul * mul;
    }
}

// 快速幂迭代写法
LL binaryPow(LL a, LL b){
    LL ans = 1;
    while(b > 0){
        if(b & 1)
            ans = ans * a;
        a = a* a;
        b >>= 1;
    }
    return ans;
}

4.6 two pointers

4.6.1 what's two pointers

• two pointers 思想：

  • 针对问题本身与序列特性（如有序性等），设置i，j两下标进行扫描（两端反向扫描，同端同向扫描）来降低复杂度

  • eg. partition过程，有序序列找a+b=n，归并排序的有序序列整合过程

4.6.2 归并排序

• 2-路归并排序

  • 核心：two pointers - 外排merge过程

• 递归过程：反复将当前区间[left,right]分成两半，对两个子区间[left,mid]，[mid+1,right]分别递归进行归并排序，然后边界条件为left=right；

• 非递归过程：步长为2的幂次，初始化=2，将每step个元素作为一组，内部进行排序，然后再将step✖2，重复操作。边界条件是step/2>n （方便代码，设数组下标=1开始）

// 归排递归

const int maxn = 100;
void merge(int A[], int L1, int R1, int L2, int R2){ //外排 两个有序数组合并成一个有序数组
    int i = L1, j = L2;
    int temp[maxn], index = 0;
    while(i <= R1 && j<= R2){
        if(A[i] <= A[j])
            temp[index++] = A[i++];
        else temp[index++] = A[j++];
    }
    while(i <= R1) temp[index++] = A[i++];  // 12389  23
    while(j <= R2) temp[index++] = A[j++];
    for(i = 0; i<index; i++)
        A[L1+i] = temp[i];
}
void mergeSort(int A[], int left, int right){
    if(left < right){
        int mid = (left + right) / 2;
        mergeSort(A,left,mid);
        mergeSort(A,mid+1,right);
        merge(A,left,mid,mid+1,right);
    }
}

// 归排非递归

void mergeSort(int A[]){
    for(int step = 2; step/2 <= n; step*=2){
        for(int i =1; i<= n; i+=step){
            int mid = i+ step/2 -1;
            if(mid+1 <=n)
                merge(A,i,mid,mid+1,min(i+step-1,n));
            // 可以用sort代替merge用来输出归排过程中某一趟的结束序列
            // sort(A+i,A+min(i+step,n+1));
        }
        //在此输出语句
    }
}

4.6.3 快速排序

• 平均时间复杂度O(nlogⁿ)

• ① 调整序列中元素，使当前序列最左端的元素在调整后满足左侧所有元素均不超过该元素，右侧所有元素均大于该元素 - partition / two pointers过程

• ② 对该元素左侧 / 右侧分别递归进行①的调整，直到当前调整区间的长度不超过1

• 最坏时间复杂度是O(n²)，但对任意输入数据的期望时间复杂度都是O(nlogⁿ)，所以不存在一组特定的数据使这个算法出现最坏情况（算法导论证明）- 随机快排，主元随机选取

• C语言生成随机数

#include<stdio.h>
#include<stdlib.h>
#Include<time.h>
int main(){
    srand((unsigned)time(NULL));    //main开头加上
    
    printf("%d",rand());    //rand()调用生成一个随机数：[0,RAND_MAX] 自定义范围：%+-*/
}

• 随机快排 = 选取随机主元 + 经典快排

// 经典快排
void quickSort(int A[], int left, int right){
    if(left < right){
        int pos = Partition(A,left,right);
        quickSort(A,left,pos-1);
        quickSort(A,pos+1,right);
    }
}

// 随机快排
int randPartition(int A[],int left, int right){
    // 生成随机数
    int p = round(1.0*rand() / RAND_MAX * (right-left) + left);
    swap(A[p],A[left]);
    
    //partition过程
    int temp = A[left];
    while(left < right){
        while(left < right && A[right] > temp) right--;
        A[left] = A[right];
        while(left < right) && A[left] <= temp) left++;
        A[right] = A[left];
    }
    A[left] = temp;
    return left;
}

4.7 其他高效技巧与算法

4.7.1 打表

• 空间换时间，一次性将可能用到结果事先求出，需要时查表；eg. 素数表求素数查表。常见打表用法：

  1. 在程序中一次性计算出所有需要用到结果，之后查表查询

     • eg. 查询大量Fibonacci数F(n)问题，预处理将所有Fibonacci存表。 - O(nQ)降O(n+Q)

  2. 当暂无思路，用暴力方法在本地运算，输出结果保存表中，再在线上根据输入查表得结果

4.7.2 活用递推

• eg. 当序列中每一位所需要计算得值都可以通过该位左右两侧结果计算得到 / 分为左右两边计算，那么就可以通过递推进行预处理得到。

• 例题：APPAPT字符串中有两个单词"PAT"。假设字符串只由P，A，T构成，现给定字符串，问一共能形成多少个"PAT"

  • 思路：遍历数组，对每一个A，看左边有多少P，右边有多少T，然后P * T得到结果，累加所有的A结果值即可
    • 用一个leftNum来存储对应位左边的P个数，rightNum来存储对应位右边的T个数：利用递归，最左边的leftNum=0，leftNum[i] = leftNum[i-1] + (if(Array[i]是不是P))；rightNum同理计算可得。时间复杂度O(n)

#include<cstdio>
#include<cstring>
const int MAXN = 100010;
const int MOD = 100000007;      // 要求输出结果对MOD取余
char str[MAXN];
int leftNumP[MAXN] = {0};
int main(){
    gets(str);
    int len = strlen(str);
    for(int i = 0; i< len; i++){
        if(i>0)
            leftNumP[i] = leftNumP[i - 1];
        if(str[i] == 'P')
            leftNumP[i]+=;
    }
    int ans = 0,rightNumT = 0;
    for(int i =len - ;i >= 0; i--){
        if(str[i] == 'T')   rightNumT++;
        else if(str[i] == 'A') ans = (ans +leftNumP[i] * rightNumT) % MOD;
    }
    
    printf("%d",ans);
    return 0;
}

4.7.3 随机选择算法

• 将集合划分成两部分左右区间：不要求区间内有序但要求的是区间内元素个数（但要考虑左边都比右边小的特性）

  • 思想类似于随机快排，一次随机partition后，主元左侧个数是确定的，右侧亦然。

  • eg. 求数组中第K大的数：正常想法是排序后取值，时间复杂度O(nlogⁿ)。若用随机选择算法，则是对数组进行随机partition，直至主元左区间元素个数为K-1，则此时主元就是第K大的数，时间复杂度O(n)

第五章 入门篇(3) - 数学问题

5.2 最大公约数与最小公倍数

5.2.1 最大公约数

• 欧几里得算法求最大公约数，设gcd(a,b)为a，b之间的最大公约数。

  • 设a，b均为正整数，a>b，则gcd(a,b) = gcd(b,a%b)

  • 递归边界：gcd(a,0)=a，n%1=0

// 直观写法
int gcd(int a, int b){
    if(b == 0) return a;
    else return gcd(b, a%b);    
}

// 简明写法
int gcd(int a, int b){
    return !b ? a : gcd(b, a%b);
}

5.2.2 最小公倍数

• 最小公倍数是可在最大公约数基础上求得

• 最小公倍数 = a * b / gcd(a,b)

  • 防止溢出：a / gcd(a,b) * b

5.3 分数的四则运算

5.3.1 分数的表示和化简

• 分数的表示

  • 结构体假分数形式，up分子，down分母

  • 规定

    • ① 负号放在分子上，分母恒正

    • ② 分数为0，则分子为0，分母为1

    • ③ 分子和分母最简，无1外其他公约数

• 分数的化简 - 写个函数专门处理化简，使分数格式符合规定

  • ① 当四则运算使分母为负时，分子分母取相反数

  • ② 当分子为0时，分母赋值为1

  • ③ 约分：分子分母同时除以非1最大公约数

5.3.2 分数的四则运算

• 分数的加法：（其他运算同此）

  • \(result = \frac{f1.up * f2.down + f2.up * f1.down}{f1.down * f2.down}\)

  • result.up = 分子 / result.down = 分母 - 计算结果再调用化简函数

• 进行除非时需要检查f2.up != 0 - result分母非零

5.3.3 分数的输出

• ① 输出分数前调用化简函数

• ② 如果分母down为1，则分数为整数，直接输出分子

• ③ 如果分子绝对值大于分母，则为假分数；

  • 整数 = r.up/r.down ； 分子 = r.up%r.down

• 除此以外说明为分数，按原样输出即可 - 为了防止溢出，分子分母一般为longlong

struct Fraction{    
    long long up,down;
}

Fraction reduction(Fraction result){ //化简函数
    if(result.down < 0){
        result.up = -result.up;
        result.down = -result.down;
    }
    if(result.up == 0)
        result.down = 1;
   esle {
        int d = gcd(abs(result.up),abs(result.down));
        result.up /= d;
        result.down /= d;
    }
    return result;
}

Fraction add(Fraction f1, Fraction f2){  //加法
    Fraction result;
        result.up = f1.up * f2.down + f2.up * f1.down;
        result.down = f1.down * f2.down;
        return reduction(result);
}

void showResult(Fraction r){
    r = reduction(r);
    if(r.down == 1) printf("%d",r.up);
    else if(abs(r.up) > r.down)
        printf("%d %d %d",r.up / r.down , abs(r.up) % r.down, r.down);
    else printf("%d / %d",r.up , r.down);
}

5.4 素数

• ① 如何判断给定正整数n是否是质数 ② 较短时间内得到1~n素数表

5.4.1 素数的判断

• O(n)：n求余2~n-1为0则非素数

• O(sqrtN)：k * (n/k) = n，n若非素数，至少也有两个约数，则一定满足一个大于一个小于sqrt(n) - 所以只要判断2~[sqrt(n)]（向下取整）余数非0

  • 两种写法，一种是sqrt(n)求出并用变量存储，另一种是直接i * i作为循环结束条件；前者安全，后者当n接近int范围上界时可能导致i * i溢出 - 解决办法就是将i改为longlong

bool isPrime(int n){    //sqrt(n)
    if(n <= 1) return false;
    int sqr = (int)sqrt(1.0*n);
    for(int i =2; i<=sqr; i++){
        if(n%i == 0) return false;
    }
    return true;
}

bool isPrime(int n){    // i * i
    if(n <= 1) return false;
    for(long long i = 2; i * i <= n; i++)
        if(n % i == 0) return false;
    return true;
}

5.4.2 素数表的获取

• O(n * sqrt(n))：遍历1~n，每个都调用O(sqrt(n))判断是否是素数，再打印；当n超过10⁵时效率较低

• O(nlog^logn)：Eratosthenes筛法（埃式筛法）

  • 思想：重点是筛。

    • 2~n-1序列，标记数组全为true，从2开始，先删去2和所有2的倍数（即令标记数组为false）；

    • 再到3，判断标记数组是否是true，删去3和所有3的倍数；

    • 再到4，判断false跳过，再到5，直至结束遍历

• O(n)：欧拉筛法（线性筛）

  • 思想：在埃式筛法的基础上，不重复设置标记，每个合数只被其最小质因子筛选一次

  • eg. 30只会被2筛选，不会被3、5等筛选，

    • 2~n-1序列，标记数组全为true，从2开始，判断标记数组true，2加入素数数组，2 * 2置为合数

    • 再到3，判断true，加入素数数组，2 * 3，3 * 3置为合数；

    • 再到4，判断false，2 * 4置为合数，退出；

  • 最重要的一步：if(i % prime[j] == 0) break; - 此时退出因为后续j+1的vis[i*prime[j+1]]对prime[j+1]而言它不是最小质因数，prime[j]是，后面其他质数更不是，所以直接退出遍历下一个

// O(n * sqrt(n))
const int maxn = 101;
int prime[maxn], pNum = 0;
bool p[maxn] = {0};
void Find_Prime(){
    for(int i =1; i < maxn; i++){
        if(isPrime(i) == true){
            prime[pNum++] = i;
            p[i] = true;
        }
    }
}

// 埃式筛法
void Find_Prime(){
    for(int i =2; i < maxn; i++){
        if(p[i] == false){
            prime[pNum++] = i;
            for(int j = i+i; j<max ; j += i)
                p[j] = true;
        }
    }
}

// 欧拉筛法(线性筛)
void Find_Prime(){
     for(int i = 2; i <= n; i++)
    {
        if(!p[i])   //不是目前找到的素数的倍数 
        prime[pNum++] = i;  //找到素数
        for(int j = 0; j<pNum && i*prime[j]<=n; j++)
        {
            p[i*prime[j]] = true;   //找到的素数的倍数不访问 
            if(i % prime[j] == 0) break;    //关键！！！！ 
        }
}

5.5 质因子分解

• eg. 20 = 2 * 2 * 5

• 用结构体数组存储十种素数 - 2 * 3 * 5...前十个素数乘积已经超过int范围，故factor数组开十个即可

  • fac[0].x = value ; fac[0].cnt = times;

• 思路 - O(sqrt(n))

  • n的质因子要么全部都小于sqrt(n)；要么只有一个大于sqrt(n)，其余均小于sqrt(n)

  • ① 遍历 2~sqrt(n)中的素数，n对素数求余，若是为0，则初始化质因子，并循环除确定其个数

  • ② 遍历完成后若n仍然大于1，则剩下的n就是大于sqrt(n)的质因子，初始化并加入factor数组即可

5.6 大整数运算

5.6.1 大整数存储

• 用int数组对大整数各位存储，高位存储高位，低位存储低位，方便遍历运算；读入数组后需要进行数组逆转
  • 比较大小：先比较位数len，再从最高位往低位比较

// 初始化
struct bign{
    int d[1000];
    int len;
    bign(){
        memset(d,0,sizeof(d));
        len = 0;
    }
}

// 读入数组
bign change(char str[]){
    bign a;
    a.len = strlen(str);
    for(int i = 0; i < a.len; i++)
        a.d[i] = str[a.len-i-1] - '0';
    return a;
}

// int compare(bign a, bign b){
    if(a.len > b.len) return 1;
    else if(a.len < b.len) return -1;
    else{
        for(int i = a.len - 1; i >= 0; i--){
            if(a.d[i] > b.d[i]) return 1;
            else if(a.d[i] < b.d[i]) return -1;
        }
    }
    return 0;
}

5.6.2 大整数的四则运算

• 加法：跟正常加法一样，个位+个位+进位

• 减法：个位 - 个位 - 借位

• 乘法：int * big 各位相乘；big * big 同上加法

• 除法：从高到低逐位相除

5.7 扩展欧几里得算法（略）

• 扩展欧几里得算法（ax + by = gcd(a,b)的求解）

• 方程ax + by = c的求解

• 同余式 ax = c(mod m)的求解

• 逆元的求解以及(b/a)%m的计算

5.8 组合数

5.8.1 关于n!的一个问题

• 求n!中有多少个质因子p - 6!中有4个质因子2

  • O(nlogⁿ)：将1~n每个数遍历各有多少个质因子p再叠加

    • 遍历数i循环除以p

  • O(logⁿ)：n!中有(n/p + n/(p<sup>2</sup>) + n/(p<sup>3</sup>) + ...)个质因子p，其中除法均为向下整除

    • 延申：n!的末尾有多少个零：等于n!中质因子5的个数

    • 推广：n!中质因子p的个数 = 1~n中p的倍数个数(n/p)加上((n/p)!)中质因子p的个数 - 递归版本求质因子p个数

//  O(nlog<sup>n</sup>)
int cal(int n ,int p){
    int ans = 0;
    for(int i = 2; i <= n; i++){
        int temp = i;
        while(temp % p == 0){
            ans++;
            temp /= p;
        }
    }
    return ans;
}

// O(log<sup>n</sup>) 非递归版本
int cal(int n , int p){
    int ans = 0;
    while(n){
        ans += n / p;
        n /= p;
    }
    return ans;
}

// O(log<sup>n</sup>) 递归版本
int cal(int n, int p){
    if(n<p) return 0;
    return n / p + cal(n / p, p);
}

5.8.2 组合数的计算

• 组合数C_n^m：从n个不同元素中选出m个元素的选法，不考虑位置

  • C(n,m) = n! / m!(n-m)!

  • C_n^m = C_n^n-m

  • C_n⁰ = C_nⁿ = 1

• ① 如何计算C_n^m

  • 方法一：通过三个阶乘的定义式计算 - n! / m!(n-m)! 即使用longlong也只能n<=21

  • 方法二：通过递推公式计算 - C_n^m = C_n-1^m + C_n-1^m-1

    • 边界条件就是让n和m一样大；或者让m变为0

    • 重复计算问题：开一个二维数组存储已经计算过的值即可

    • 递归写法计算单个C(n,m)小于O(n²) 与 非递归写法(递推写法)计算所有C(n,m)复杂度O(n²)

  • 方式三：通过定义式的变形来计算

    • \(C_{n}^{m} = \frac{n!}{m! * (n-m)!} = \frac{(n-m+1) * (n-m+2) * ... * (n-m+m)}{1 * 2 * 3 ... * m}\)

    • \(\frac{(n-m+1) * (n-m+2) * ... * (n-m+m)}{1 * 2 * 3 ... * m} = \frac{\frac{\frac{n-m+1}{1} * (n-m+2)}{2}* (n-m+2)}{3}...\)

    • (n-m+1) * (n-m+2)... * (n-m+i) / (1 * 2 ... * i) = C_n-m+iⁱ一定是个整数；所以上述变形式就可以保证不会在边乘边除的过程中出现小数导致误差的情况 - 由于除法故保证避免了溢出问题，n<=62左右，时间复杂度O(m)

// 方法一
long long C(long long n, long long m){
    long long ans = 1;
    for(long long o = 1; i <= n; i++)
        ans *= 1;
    for(longlong i = 1; i <= m; I++)
        ans /= i;
    for(long long o = 1; i <= n - m; i++)
        ans /= i ;
    return ans;
}

// 方式二 - 递归
long long res[67][67] = {0};
long long C(long long n, long long m){
    if(m == 0 || m == n) return 1;
    if(res[n][m] != 0) return res[n][m];
    return res[n][m] = C(n-1,m) + C(n-1,m-1);
}

// 方式二 - 递推
const int n = 60;
void calC(){
    for(int i = 0; i <= n; i++)
        res[i][0] = res[i][i] =1;
    for(int i = 2; i <= n; i++)
        for(int j = 0; j <= i/2; j++)}
            res[i][j] = res[i-1][j] +res[i-1][j-1];
            res[i][j-1] = res[i][j] ;
        }
}

// 方法三
long long C(long long n, long long m){
    long long ans = 1;
    for(long long i = 1; i<=m; i++)
        ans =ans * (n-m+i) / i;
    return ans;
}

• ② 如何计算C_n^m%p

  • 方法一：通过递推公式计算，基于第一问的方法二，只需要在原代码上对p取模即可

    • 也是分成递归与递推两种代码实现

  • 方法二：根据定义式计算 - 将组合数C_n^m进行质因子分解，计算每一组质因子p_i^cut%p相乘再取模即可 - 利用5.8.1中的方法对n!，m!，(n-m)!分别计算含质因子p的个数x,y,z，C_n^m中的质因子个数为x-y-z。

    • 时间复杂度O(klogⁿ)，其中k不超过n的质数个数

  • 方法三：通过定义式的变形计算（略）

  • 方法四：Lucas定理(卢卡斯)（略）

// 方法一 - 递归
int res[1010][1010] = {0};
int C(int n, int m, int p){
    if(m == 0 || m == n) return 1;
    if(res[n][m] != 0) retirm res[n][m];
    return res[n][m] = (C(n-1,m) + C(n-1,m-1)) % p;
}

// 方法一 - 递推
void calC(){
    for(int i =0; i <= n; i++)
        res[i][0] = res[i][i] =1;
    for(int i =2; i <= n; i++)
        for(int j = 0; j <= i / 2; j++){
            res[i][j] = (res[i-1][j] + res[i-1][j-1]) % p;
            res[i][i-j] = res[i][j];
        }
}

// 方法二
int prime[maxn];

int C(int n ,int m ,int p){
    int ans = 1;
    for(int i = 0; prime[i] <= n; i++){
        int c = cal(n,prime[i]) - cal(m,prime[i]) - cal(n-m,prime[i]);
        ans = ans * binaryPow(prime[i],c,p) % p;
    }
    return ans;
}

//方法四
int Lucas(int n ,int m){
    if(m == 0) return 1;
    return C(n % p,m % p) * Lucas(n / p, m / p) % p;
}

图片

第六章 C++标准模板库(STL)

6.1 vector的常见用法详解

• #include<vector> using namepsace std;

  • vector name;

  • vector<vector > name; // >>之间要加空格

  • vector Array[Size];

• 容器内元素访问

  • 通过下标访问：vi[i] - 同数组

  • 通过迭代器访问：vector::interator it; //迭代器使用类似于指针

    • it = vi.begin() //取vi首元素地址，it指向这个地址 vi.end()：尾元素的下个地址

    • vi[i] = * (it+i) //指针一样用 * 来遍历向量元素 - 只有vector和string才允许迭代器+整数的写法

    • it++ / ++it

// 迭代器遍历 - 方式一
vector<int>::iterator it = vi.begin();
for(int i = 0; i<5; i++)
    printf("%d",*(it+i));   //*(it+i)输出vi[i]

// 迭代器遍历 - 方式二
for(vector<int>::iterator it = vi.begin(); it != vi.end(); it++)    //vector迭代器不支持it<vi.end()写法，故只能用it!=vi.end()
    printf("%d",*it);

• vector常用函数实例

  • size()：返回vi中元素个数，unsigned，时间复杂度O(1) - 都通用

  • push_back(x)：在vector后添加一个元素x，时间复杂度O(1)

  • pop_back()：删除vector尾元素，时间复杂度O(1)

  • clear()：清空vector中所有元素，O(N) - 都通用

  • insert(it,x)：在迭代器位置处插入一个元素

  • erase()：删除迭代器处单个元素erase(it) - 删除迭代器地址区间元素erase[first,last)

    • eg. vi.erase(vi.begin(),vi.begin()+3); // 删除vi[0],vi[1],vi[2]

    • vi.erase(vi.begin(),vi.end()) = vi.clear()

• vector常见用途：

  • ① 储存数据 ② 用邻接表存储图

6.2 set的常见用法详解

• 内部自动递增有序且不含重复元素

• #include<set> using namespace std;

  • set name; // 注意事项与vector相同

• set容器内元素访问：

  • set只能通过迭代器访问： set<typename>::interator it;

  • 不支持 * (it+i)访问，只能用it++形式遍历集合

• set常用函数实例

  • insert(x)：将x加入集合，时间复杂度O(logN)

  • find(x)：返回set中x对应的迭代器，时间复杂度O(logN) - *(st.find(x));

  • erase()：删除单个元素有两种方法；删除区间内元素同vector，时间复杂度O(last-first)

    • 一是删除迭代器位置元素O(1)，可以结合find()来使用：st.erase(st.find(100));

    • 二是删除集合对应值O(logN)

• set常见用途：① 自动去重并升序 ② STL用红黑树实现。C++11中新加unordered_set用散列实现，去重但不排序；multiset排序但不去重

6.3 string的常见用法详解

• #include<string> using namespace std;

• string内容访问

  • printf%s + str.c_str() 输出

  • 下标访问str[i]

  • string迭代器：string::iterator it;

    • 支持it++与*(it+k)

• string常用函数实例

  • operator+=：string拼接操作符 eg. str1+=str2

  • compare：== != < >等比较运算符 - 字典序比较

  • length() / size()

  • erase() - 删除单个元素和删除区间元素，时间复杂度都是O(n)

    • 删除单个元素：str.erase(it)删除迭代器位置处元素

    • 删除区间元素：str.erase(first,end) - 起始迭代器，末尾下个位置迭代器区间；str.erase(pos,len) - 索引下标起删除len个元素

  • clear()：清空所有元素

  • substr(pos,len)：截取子串函数，从pos索引下标截取len个字符子串

  • find() + string::npos：查找匹配子串函数，时间复杂度O(nm)，分别是str/str2长度；string::npos是find失配返回值，为-1/unsigned_int类型最大值

    • find(str2)：str1的前缀查询str2子串，返回第一个匹配位置

    • find(str2,pos)：在str1索引下标pos起查询str2子串

    • if(str1.find() != string::npos)

  • replace()：部分串替换函数，时间复杂度为O(str1)，时间复杂度O(str.length())

    • str1.replace(pos,len,str2)：把str1的pos起len长度子串替换为str2

    • str1.replace(it1,it2,str2)：把str1迭代器[it1,it2)范围的子串替换为str2

6.4 map的常用用法详解

• #include<map> using namespace std;

  • map<typename1,typename2> mp;

  • 数组不能作为键传入map

• map容器内元素访问

  • 通过下标访问：map[键] - 值

  • 通过迭代器访问：map<typename1,typename2>::iterator it

    • it->first访问键，it->second访问值

  • map内部是使用红黑树实现，故键会自动递增排序。

• map常用函数实例解析

  • find(key)：返回键为key的迭代器，时间复杂度O(logN)

  • erase()：删除单个元素，删除区间内元素

    • mp.erase(it)：删除迭代器处元素，O(1)

    • mp.erase(key)：删除key键的元素，时间复杂度O(logN)

    • mp。erase(first,end)：删除起始迭代器，末尾下个位置迭代器区间元素，O(first-last)

  • size()：获得map大小，O(1)

  • clear()：清空map中所有元素

• map常见用途：

  • 键值映射，字典哈希

  • 判断大整数等其他类型数据是否存在的问题，可以把map当作bool数组使用

  • multimap单键映射多值，C++11中unordered_map用散列代替红黑树，无序但是速度更快

6.5 queue的常见用法详解

• queue队列，先进先出容器

• #include<queue> using namespace std;

  • queue name;

• queue容器内元素访问

  • 先进先出限制性结构，front()访问队首元素，back访问队尾元素

• queue常用函数实例解析

  • push()：队列元素入队，O(1)

  • front()、back()：获得队首队尾元素

  • pop()：队首元素出队，O(1)

  • empty()：检测queue是否为空，true为空false非空，O(1)

  • size()：返回queue内元素个数，O(1)

• queue的常见用途：

  • 广搜BFS使用队列

  • 使用front/back()前需要empty()判空

  • 双端队列(deque)：两端插入删除 - 优先队列(priority_queue)：默认大根堆实现的队列

6.6 priority_queue的常见用法详解

• 优先队列，底层使用堆来实现，默认使用大根堆，优先规则可以自定义

• #include<queue> using namespace std;

  • priority_queue name;

• priority_queue容器内元素访问：

  • 优先队列通过top()函数来访问队首元素/堆顶元素

• priority_queue常用函数实例解析

  • push(x)：x元素入队，调整堆，O(logN)

  • top()：获得队首/堆顶元素，O(1)

  • pop()：队首/堆顶元素出队，O(logN)

  • empty()：判断优先队列是否为空，true为空false非空，O(1)

  • size()：返回队列大小，O(1)

• priority_queue内元素优先级自定义：

  • 基本数据类型优先级设置：默认大根堆

    • priority_queue<int> q; 默认大根堆

    • priority_queue<int, vector<int>, less<int> > q; 自定义数字越大优先级越大 - vector填写的是承载底层数据结构heap的容器，less则是int的比较参 - less<>数越大优先级越高，greater<>数越小优先级越高

  • 结构体的优先级设置：（写在结构体内）在结构体里面重载 "<"（>是<相对，需要加友元），returnTrue则后者优先级更大，returnFalse则前者优先级更大（传入两个结构体参数）

  • 类似于sort函数中cmp函数，作用实则是相反的，因为优先队列本身默认是优先级高的在队首，重载<是cmp反向效果

    • 若是想写在结构体外，则另用一个结构体存储重载小括号()。结构体内的话则声明定义时默认是重载优先级，而结构体外定义时是需要像less一样传出参数定义。

// 基本数据类型
priority_queue<int, vector<int>, less<int> > q;
priority_queue<int, vector<int>, greater<int> > q;

// 结构体自定义优先级 - 结构体内

struct fruit{
    string name;
    int price;
    friend bool operator < (const fruit &f1, const fruit &f2){
        return f1.price < f2.price;  // 数越大优先级越高
        // return f1.price > f2.price;  数越小优先级越高
    }
}

// 结构体自定义优先级 - 结构体外
struct cmp{
    bool operator () (const fruit &f1, const fruit &f2){
        return f1.price < f2.price;  // 数越大优先级越高
        // return f1.price > f2.price;  数越小优先级越高
    }
}
// 定义优先队列
priority_queue<fruit, vector<fruit>,cmp > q;

• priority_queue的常用用途：

  • 使用优先队列解决贪心问题，也可以对Dijkstra迪杰斯特拉算法进行优化（因为本质是堆）

  • 使用top()函数前，必须用empty()判空。

6.7 stack的常见用法详解

• #include<stack> using namespace std;

  • stack name;

• stack容器内元素的访问

  • 只能通过top()函数获得栈顶元素

• stack常用函数实例解析：

  • push(x)：x元素入栈，O(1)

  • top()：获取栈顶元素，O(1)

  • pop()：弹出栈顶元素，O

  • empty()：判空，true空false非空

  • size()：返回stack大小

• stack常见用途：

  • 用来模拟递归过程，防止对程序栈内存的溢出。

  • 用stack实现DFS

6.8 pair常见用法详解

• 作为一种简约的结构体，实现二元组的功能。

• #include<utility> using namespace std;

  • map的内部实现中使用了pair容器，故#include
  • pair<type1,type2> name;

    • 定义初始化：pair<string,int> p1("hah",25)

    • 两种方式创建临时量：pair<string,int>("hah",25) / make_pair("hah",25)

• pair容器内的元素访问：

  • p.first / p.second

• pair常用函数解析：

  • 比较操作符：< > == ... 两个pair容器可以进行比较运算，first相同再是second比较（如果first/second可以进行比较运算的话）

• pair的常见用途：

  • ① 用来代替二元结构体及其构造函数，可以节省编码 ② 作为map的键值对插入：mp.insert(make_pair("hah",25)) / mp.insert(pair<string,int>("hah",25))

6.9 algorithm头文件下的常用函数

• #include<algorithm> using namespace std;

6.9.1 max(),min(),abs()

• max / min比较两数之间的最大最小值，允许浮点数比较；三个数比较则写成max(a,max(b,c))

• abs()返回整数的绝对值，浮点数使用math库下的fabs()函数

6.9.2 swap()

• swap(a,b)，交换ab两数的值

6.9.3 reverse()

• 逆序函数
  • reverse(it1,it2)：it为数组下标地址或容器迭代器，逆序[it1,it2)位置元素

int a[10] = {1,2,3,4,5,6,7,8,9,10};
reverse(a,a+4);  // 将a[0]~a[3]逆序
for(...){printf("%d"),a[i]};    //4321 5678910

string str = "abcdefg"
reverse(str.begin,str.begin+3)  // 将str[0]~str[2]逆序
printf("%s",str.c_str())    // cbadefg

6.9.4 next_permutation()

• 给出一个序列在其元素全排序中的下一个序列

  • eg. 231在全排列中的下一个序列为312

• next_permutation(it1,it2)：it同逆序函数，本身返回true/false，true表示有下个序列，并会对传入参数进行更改成下个序列；false表示传入参数已是全排序的最后一个序列了。

int a[10] = {1,2,3};
do{
    for(...) printf("%d",a[i]);
}while(next_permutation(a,a+3))

6.9.5 fill()

• 可以把数组或容器内某段区间赋值成相同的任意值（区别memset - 只能填充数组为0/-1）

• fill(it1,it2,x) - (it1,it2]区间填充x值

6.9.6 sort()

• sort(it1,it2,[cmp]) - cmp非必填自定义排序函数，默认递增

• cmp函数：returnTrue则一参前二参后；returnFalse则二参前一参后

  • 基本数据类型：bool cmp(int a, int b){...}

  • 结构体类型：bool cmp(const node *a, const node *b){...}

  • 容器类型：只有vector、string和deque()（双端队列）可以使用sort，其他类型内部是由红黑树实现，已是有序。

    • 双端队列和vector的cmp是根据元素类型 - eg. vector使用的cmp是基本数据类型int的cmp

    • string：bool cmp(string str1, string str2){...}

6.9.7 lower_bound(), upper_bound()

• 需要使用在有序数组/容器中

  • lower_bound(first,end,val)寻找数组或容器[first,end)中第一个大于等于val的元素位置，返回指针(地址)或者迭代器；

  • unper_bound(first,end,val)寻找数组或容器[first,end)中第一个大于val的元素位置

  • 在4.5.1节中详细表述了其内部实现，使用的是二分实现；若是没有找到，则均返回插入val的位置地址/迭代器，时间复杂度O(log(first-end))

第七章 提高篇(1) - 数据结构专题(1)

7.1 栈的应用

• 先入后出，栈顶指针top：指向栈顶元素索引，栈为空时top=-1

• 常见操作实现：

  • clear()清空：令top=-1即清空栈

  • size()栈大小：top值+1即为栈大小

  • empty()判空：top==-1时判空返回true

  • push()进栈：先判空，再st[++top]=x

  • pop()出栈：先判空，再top--即可

  • STL库中的栈没有实现clear()操作，所以clear()操作需要自己去写一个：while(!st.empty()){st.pop();} - 通常直接再new一个栈，用空间换时间

7.2 队列的应用

• 先进先出，队首指针front指向队首元素前一个，队尾指针rear指向队尾元素

• 常见操作实现：

  • clear()清空：令front=rear=-1

  • size()队列大小：size = front-rear

  • empty()判空：front==rear，出对入队取数前需要判空

  • push()入队：q[++rear] = x

  • pop()出队：front++

  • get_front()取队首元素：q[front+1]

  • get_rear()取队尾元素：q[rear]

  • • STL库中的队列没有实现clear()操作，所以clear()操作需要自己去写一个：while(!q.empty()){q.pop();} - 通常直接再new一个队列，用空间换时间，O(1)

7.3 链表处理

7.3.1 链表的概念

• 线性表分为顺序表(数组)和链表两种
  • 数组分配连续地址空间，链表分配不连续地址空间

struct node{
    typename data;
    node* next;
};

• 头节点head，数据域为空，指针域指向第一个节点

7.3.2 使用malloc / new分配内存空间

• malloc函数（C

  • #include<stdlib.h>

    • typename* p = (typename*)malloc(sizeof(typename));

    • malloc返回的是void* 类型，再给前面加一个强制类型转换

• new运算符（C++

  • typename* p = new typename; // node* p = new node;

  • typename* p = new typename[num]; // int* p = new int[100]

• 内存泄漏：使用malloc/new申请的空间没有及时释放 - 在C/C++中申请的空间必须将其释放

  • (1) free函数（C

    • 同样在stdlib.h头文件下，直接调用free(p);，与malloc成对存在

  • (2) delete函数（C++

    • delete(p);，与new承兑存在

7.3.3 链表的基本操作

• 创建链表：node* create(int Array[]); 将每个节点新建并加入

// 创建链表
node* create(int Array[]){  // Array是数据域
    node *p, *pre, *head;   //pre保存当前节点前驱节点，head为头节点
    head = new node;
    head->next = NULL;
    pre = head;
    for(int i = 0; i<5; i++){    //Array的长度
        p = new node;
        // 将Array[i]赋值给新建节点，也可以scanf输入
        p->data = Array[i];
        p->next = NULL;
        pre->next = p;
        pre = p;
    }
    return head;
}

// 遍历链表
while(L != NULL){
    priintf("%d",L->data);
    L = L->next;
}

• 查找元素：int search(node* head, int x); 遍历一遍链表查找元素次数

// 在以head为头节点的链表上计数元素x的个数
int search(node* head, int x){
    int count = 0; //计数器
    node* p = head->next;
    while(p != NULL){       // 遍历
        if(p->data == x)
            count++;
        p = p->next;
    }
    return count;
}

• 插入元素：void insert(node* head, int pos, int x); 在第n位置上插入x，就是第n个变成x - 两步操作

void insert(node* head, int pos, int x){
    node* p = head;
    for(int i = 0; i < pos-1; i++)
        p = p ->next;    //pos-1是为了到插入位置的前一个节点
    node* q = new node;
    q->data = x;
    q->next = p->next;      // 插入元素只需要改变两个next即可
    p-next = q;
}

• 删除元素：void del(node* head, int x); 删除链表上值为x的节点 - 三步操作

void del(node* head, int x){
    node* p = head->next;
    node* pre = head;   //pre指向前驱节点
    while(p != NULL)
        if(p->data == x){       //删除p
            pre->next = p->next;
            delete(p);
            p = pre->next;
       } else {     // 如果不是要删除的元素，则pre/p都往后移
            pre = p;
            p = p->next;
       }
}

7.3.4 静态链表

• 当节点地址是比较小的整数时，用的更多的是静态链表 - hash思想解决链表问题

  • 实现原理是hash，通过建立一个结构体数组，下标表示节点的地址，用来直接访问节点值。

  • 指针域改为int类型，保存next节点的下标值，若值为-1则表示NULL - 从而构造成一个hash映射（改进甚至可以直接用一个hashmap来存储next关系）

  • 在使用静态链表时，尽量不要把类型名和变量名命名成相同名字，防止sort函数编译出错

  • （对于这类题目在牛客网算法课上有提及，可以保持原来动态链表形式，加入一个hashmap进行映射构造，可以使代码更加直观易理解）

• 定义静态链表模板：

struct Node{
    int address;    //节点地址
    typename data;   //数据域
    int next;   //指针域
    XXX;        //某个节点性质，比如是否为交叉节点：bool flag;
}node[100000];

• 静态链表初始化模板：

for(int i = 0; i < maxn; i++){
    ...
    ...
    node[i].XXX = ???;
}

• 统计节点数组中的有效节点模板：

int p = begin, count = 0;
while(p != -1){     // -1代表链表结束
    ...
    ...
    count++;
    p = node[p]-next;
}

• 将有效节点放置在数组前面，并根据XXX性质从小到大排序模板：

bool cmp(Node a, Node b){
    if(a.XXX == -1 || b.XXX == -1){
        //至少有一个节点是无效节点，放到数组后面
        return a.XXX>b.XXX;
    } else{
        //第二级排序（都是有效节点的排序）
    }
}

第八章 提高篇(2) - 搜索专题

8.1 深度优先搜索(DFS)

• 深搜是一种枚举所有完整路径以遍历所有情况的搜索方法

  • 使用栈+set来实现（是一种递归的思想）- 在本书这节中，深搜≈暴力递归

• 一类问题：整数背包问题 - 递归实际上就是深搜

  • 暴力递归时间复杂度O(2ⁿ)，如果要在递归基础上降低复杂度，则需要采取剪枝

  • 通过题目条件的限制来节省DFS/递归计算量的方法称为剪枝（前提是剪枝后算法仍然正确）

  • 两个变量：当前index下标和当前sumW总重量，边界条件return当前sumC总价值 - 根据这些改成动态规划

• 一类问题：枚举从N个整数中选择K个数的所有方案 - 最优子序列

  • eg. 枚举给定序列的所有子序列；从给定序列中选择两个数使其和为6等等

  • 同样也是两个变量：当前index下标和当前sum所求目标，边界条件returnTemp方案or其他 - 同样也是可以改成动态规划用空间换时间

// 整数背包问题DFS - 类比牛客网算法讲暴力递归与动态规划那章
void DFS(int index, int sumW, int sumC){        //实际上可以把边界条件都提出放前面，写法更简便直观
    if(index == n)  return;     //边界条件1选完了
    DFS(index+1, sumW, sumC);   //不选
    if(sumW+w[index] <= V)      // 边界条件2超出了{
        if(sumC+c[index] > ans)
            ans = sumC + C[index];  //更新
        DFS(index + 1,sumW+w[index], sumC+c[index]);
    }
}

8.2 广度优先搜索(BFS)

• 广搜总是先一次访问最先能直接到达的所有节点
  • 使用队列+set来实现 - 初始点入队，出队，出度邻接点检测，未在set的点入队依次循环

void BFS(int s){
    queue<int> q;
    q.push(s);
    while(!q.empty()){
        取出队首元素top;
        访问队首元素top;
        将队首元素出队;
        将top的下一层节点中未曾入队的节点全部入队，并设置为已入队;
    }
}

• 例题：给出一个mxn的矩阵，矩阵中的元素为0或1。(x,y)与上下左右四个位置相邻，如果矩阵中有若干个1是相邻的，则称构成了一个块。求给定矩阵中的块数。

  • 基本思想：遍历每个位置元素，如果没有加入set则看值，为0则跳过，为1视为与上下左右都是相连接的通路，将其加入队列，进行BFS查询过程。遍历完后BFS查询过几次则有几个块

  • 下述代码使用的是bool数组作为set使用，用来两个增量数组来表示四个方向：int x[] = {0,0,0,1,-1} 和int y[] = {1,-1,0,0}，然后用for循环来枚举四个方向，以确定与当前坐标(nowX,nowY)相邻的四个位置

// 书本所示代码有点过于繁杂
#include<cstdio>
#include<queue>
using namespace std;
const int maxn = 100;
struct node{
    int x,y;    //位置(x,y)
}Node;

int n , m;
int matrix[maxn,maxn];      // 图矩阵
bool inq[maxn][maxn] = {false}  // set作用的bool数组
int X[] = {0,0,1,-1};
int Y[] = {1,-1,0,0};

bool judge{int x, int y}{       // 判断坐标（x,y）是否需要访问
    //越界返回false
    if(x >= n || x < 0 || y >= m || y < 0) return false;
    //当前位置为0，或(x,y)已入队，返回false
    if(matrix[x][y] == 0 || inq[x][y] == true) return false;
    //以上都不满足时返回true
    return true;
}

//BFS函数访问位置(x,y)所在块，并将该块中所有1的inq都设为true
void BFS(int x,int y){
    queue<node> Q;
    Node.x = x, Node.y = y;
    Q.push(Node);
    inq[x][y] = true;
    while(!Q.empty()){
        node top = Q.front();       // 取出队首元素
        Q.pop();    //出队
        for(int i = 0 ; i < 4; i++){
            int newX = top.x + X[i];
            int newY = top.y + Y[i];
            if(judge(newX,newY)){
                //设置Node坐标为(newX,newY)
                Node.x = newX,Node.Y = newY;
                Q.push(Node);
                inq[newX][newY] = true;
            }
        }
    }
}

int main(){
    scanf("%d%d",&n,&m);
    for(int x=0; y < n; x++)
        for(int y = 0; y < m; y++)
            scanf("%d",&matrix[x][y])   // 读入01矩阵
    int ans = 0;    //块数
    for(int x = 0; x < n; x++)
        for(int y = 0; y < m; y++)
            if(matrix[x][y] == 1 && inq[x][y] == false){
                ans++;
                BFS(x,y);
            }
    printf("%d\n",ans);
    return 0;
}

• 当在BFS使用queue时，元素入队的push操作只是创建了该元素的一个副本入队，而不是引用/指针，所有对队列中的元素进行修改并不会对原数据造成影响，反之亦然。
  • 故在使用queue时，通常加入的是元素下标而不是元素本身。

第九章 提高篇(3) - 数据结构专题(2)

9.1 树与二叉树

9.1.1 树的定义与性质

• 树tree 结点node 根结点root 叶子结点leaf 子结点child 子树subtree 边edge

  • empty tree空树：没有结点

  • layer树的层次：根结点为第一层，根结点子树的根结点为第二层

  • 结点的子树棵数称为结点的度degree，最多度结点的度称为树的度(树的宽度)

  • 有n个结点的树，边数一定是n-1，且满足连通，边数=顶点数-1的结构一定是一棵树

  • 叶子结点定义为度为0的结点，当树只有一个结点时，根结点也算作叶子结点

  • 结点的深度depth是指从根结点（深度为1）开始自顶向下逐层累加至该节点的深度值；结点的高度height是指从最底层叶子结点（高度为1）开始自底向上逐层累加至该节点的高度值

  • 多棵树的集合称为森林

9.1.2 二叉树的递归定义

• 二叉树的存储结构：二叉树一般使用链表定义（二叉链表）

  • 结点定义node

  • 新建结点newNode

  • 结点查找与修改数值search

  • 结点插入（按中序插入）insert

  • 二叉树的创建create

  • 一般是root/node = null，即地址为空，表示没有结点。

// 结点定义
struct node{
    typename data;  //数据域
    node* lchild    //指向左子树根结点的指针
    node* rchild    //指向右子树根结点的指针
}；

node* root = null;

// 新建结点
node* newNode(int v){
    node* Node = new node;
    Node->data = v;
    Node->lchild = Node->rchild = null;
    return Node;
}

// 结点的查找与修改
void search(node* root, int x, int newdata){
    if(root == null) return;    //空树
    if(root->data == x) root->data = newdata;   //找到
    search(root->lchild, x, newdata);
    search(root->rchild, x, newdata);
}

// 结点插入
void insert(node* &root, int x){
    if(root == null){    //边界条件，插入位置
        root = newNode(x);
        return;
    }
    if(由二叉树的性质，x应该先插在左子树)       // 根据所需构造二叉树的性质确定条件
        insert(root->lchild, x);
    else insert(root->rchild, x);
}

// 二叉树的创建
node* create(int data[],int n){
    node* root = null;
    for(int i = 0; i < n; i++)
        insert(root,data[i]);
    return root;
}

• 完全二叉树的存储结构：

  • 使用数组存储结点，存放顺序为该完全二叉树的层序遍历序列

  • i号结点的左右孩子分别为，node[2i] & node[2i+1]（下标0不存放元素）

  • 判断某个结点是否为叶子结点：该节点的左子结点下标是否大于结点总个数

  • 判断某个结点是否为空结点：该结点的下标是否大于结点总个数

9.2 二叉树的遍历

• 先序中序后序层序，前三种使用深搜实现（实际上就是递归），后一种使用广搜

9.2.1 先序遍历

• 先序遍历序列的性质：序列的第一个一定是根结点

void preorder(node* root){
    if(root == NULL)        // 边界条件
        return 
    printf("%d\n",root->data);      //根结点
    preorder(root->lchild);
    preorder(root->rchild);
}

9.2.2 中序遍历

• 中序遍历序列的性质：可以通过根结点划分出左子树与右子树

void inorder(node* root){
    if(root == null)    return;
    inorder(root->lchild);
    printf("%d\n",root->data);
    inorder(root->child);
}

9.2.3 后序遍历

• 后序遍历序列性质：序列最后一个一定是根结点；无论是先序还是后序，都必须知道中序才能唯一确定一棵树。

void postorder(node* root){
    if(root == null)    return;
    postorder(root->lchild);
    postorder(root->rchild);
    printf("%d\n",root->data);
}

9.2.4 层序遍历

• 对一般二叉树而言，层序遍历就是BFS广搜过程：（因为是二叉树所以不需要set）

  • root加入队列，取出队首访问，如有左右孩子，入队，循环取队首，直至队列为空。

• 很多题目要求计算出每个结点所处的层次，那么就需要在node结点定义中添加一个层次变量layer

// 层序遍历
void LayerOrder(node* root){   // 以下注释代码行为如需要输出结点层次的层序遍历代码
    queue<node*> q;
    // root->layer = 1
    q.push(root);
    while(!q.empty()){
        node* now = q.front();
        q.pop():
        printf("%d",now->data);
        if(now->lchild != null){
            //now->lchild->layer = now->layer + 1;
            q.push(now->lchild);
        }
        if(now->rchild != null){
            //now->rchild->layer = now->layer + 1;
            q.push(now->rchild);
        }
    }
}

9.2.4 (补)通过先序/后序+中序重建二叉树/求层序遍历

• 题目一：先序+中序重建二叉树（后序/层序思路同理）
  • 思路：

    • 通过先序序列的首元素pre¹找到中序序列in^k，划分in¹-in^k-1为左子树，in^k+1-inⁿ为右子树

    • 假设先序左右边界为[preL,preR]，中序边界为[inL,inR]

    • 左子树结点个数numLeft=k-1，此时先序序列再遍历k-1个，可知遍历出来的是先序序列的左子树，剩余的就是右子树；再对先序左子树和先序右子树递归以上操作（中序左右子树也都确定了）

    • 边界条件就是当先序序列长度小于等于0时结束 - preL>preR

node* create(int preL, int preR, int inL, int inR){
    if(preL > preR) return NULL;
    node* root = new node;
    root->data = pre[preL];
    int k;
    for(k = inL; k <= inR; k++)
        if(in[k] == pre[preL])  break
    int numLeft = k - inL;
    
    root->lchild = create(preL + 1,preL + numLeft, intL, k - 1);
    root->rchild = create(preL + numLeft + 1, preR, k + 1, inR);
    
    return root;
}

• 结论：中序可以跟先序，后序，层序任何一个来构建唯一二叉树，构建二叉树必须需要中序遍历。原因是：先序，后序，层序均是提供根结点，作用是相同的，都必须由中序序列来区分呢左右子树。

  • 层序遍历：第一个是根结点，第二个左子树根结点，第三个是右子树根结点，第四个是左子树的左子树根结点....思路大致相同也是递归

  • 后序遍历：最后一个是根结点，前面是左子树和右子树，所以思路与先序遍历同理

• 题目二：后序+中序输出层序遍历（就是重建二叉树，再BFS层序输出）

  • 思路：就是之前说过的一样

// 后序+中序重建二叉树
node* create(int postL, int postR, int inL, int inR){
    if(postL > postR)   return NULL;
    node* root = new node;
    root->data = post[postR];
    int k;
    for(k = inL; k <= inR; k++)
        if(in[k] == post[postR])    break;
    int numLeft = k - inL;
    root->lchild = create(postL, postL + numLeft - 1, inL, k - 1);
    root->rchild = create(polstL+numleft, postR - 1 , k + 1, inR);
    return root;
}

9.2.5 二叉树的静态实现

• 静态二叉链表是指：结点的左右指针使用int代替，用来表示左右子树根结点在数组中的下标 - 类似于静态链表，使用一个node型数组存储。

• 以下为静态二叉树的定义与操作：

struct node{
    typename data;
    int lchild;
    int rchild;
}Node[maxn];

int index = 0;
int newNode(int v){
    Node[index].data = v;
    Node[index].lchild = -1;
    Node[index].rchild = -1;
    return index++;
}

void search(int root, int x, int newdata){
    if(root == -1)  return;
    if(Node[root].data == x)    Node[root].data = newdata;
    search(Node[root].lchild, x, newdata);
    search(Node[root].rchild, x, newdata);
}

void insert(int &root, int x){
    if(root == -1){
        root = newNode(x);
        return;
    }
    if(由二叉树的性质x应该插在左子树)
        insert(Node[root].lchild, x);
    else insert(Node[root].rchild, x);
}

int Create(int data[], int n){
    int root = -1;
    for(int i = 0; i < n; i++)
        insert(root, data[i]);
    return root;
}

void preorder(int root){
    if(root == -1)  return;
    printf("%d\n", Node[root].data);
    preorder(Node[root].lchild);
    preorder(Node[root].rchild);
}

void inorder(int root){
    if(root == -1)  return;
    inorder(Node[root].lchild);
    printf("%d\n", Node[root].data);
    inorder(Node[root].rchild);
}

void postorder(int root){
    if(root == -1)  return;
    postorder(Node[root].lchild);
    postorder(Node[root].rchild);
    printf("%d\n", Node[root].data);
}

void LayerOrder(int root){
    queue<int> q;
    q.push(root);
    while(!q.empty()){
        int now = q.front();
        q.pop();
        printf("%d\n", Node[root].data);
        if(Node[now].lchild != -1) q.push(Node[now].lchild);
        if(Node[now].rchild != -1) q.push(Node[now].rchild);
    }
}

9.3 树的遍历

9.3.1 树的静态写法

• 树的一般意义上定义：即子结点个数不限且子结点没有先后次序的树。

  • 静态表示所有树结点存储在数组中Node[maxn]

  • 树的静态写法：指针域使用STL中的vector来存储所有子结点

struct node{
    typename data;
    vector child;
}Node[maxn];

// 新建结点
int index = 0
int newNode(int v){
    Node[index].data = v;
    Node[index].child.clear();
    return index++;     //返回结点下标
}

9.3.2 树的先根遍历

• 类似于二叉树的先序遍历，DFS递归访问树的所有结点 - 先根结点后子结点
  • 其边界条件暗含在for循环中

void PreOrder(int root){
    printf("%d",Node[root].data);
    for(int i = 0; i < Node[root].child.size(); i++)
        PreOrder(Node[root].child[i]);
}

9.3.3 树的层序遍历

• 树的层序遍历思路与二叉树的层序遍历一样，都是从树根结点开始一层一层遍历，BFS查询。

void LayerOrder(int root){
    queue<int> Q;
    Q.push(root);
    Node[root].layer = 0;   //后续代码会输出结点所在层
    while(~Q.empty()){
        int front = Q.front();
        printf("%d",Node[front].data);
        Q.pop();
        for(int i = 0; i < Node[front].child.size(); i++){
            int child = Node[front].child[i];
            Node[child].layer = Node[front].layer+1;
            Q.push(child);
        }
    }
}

9.3.4 从树的遍历看DFS和BFS

• 深搜DFS与先根遍历：

  • 对所有合法的DFS求解过程都可以化成树的形式，遍历过程就是树的先根遍历过程；求解树的某些信息也可以用DFS深搜来对结点进行遍历获得信息。

  • eg. 求叶子结点的带权路径和，深度是关键词

  • 深搜+剪枝，剪枝就是对暴力递归的优化，通过已知条件的限制，来确定某些不需要通过的路径/可以忽略的子树从而将其剪断。

• 广搜BFS与层序遍历

  • 同上理，对所有合法的BFS求解过程也可以转为对树的层序遍历，对树关于广度的一些信息也可以通过BFS来获取。

• 题目：求叶子结点的路径和问题

  • 题意：给定一棵树和每个结点权值，求所有的叶子结点路径和，使得和为给定常数S。如果有多条这样的路径非递增输出。 - 如有a1-a2-..an和b1-b2-..bm，且有ai>bi，前面都相等，则a>b

  • 思路：

    • 对于非递增输出，只需要将vector进行sort排序从大到小即可，这样就能保证输出的路径是非递增的 - 在定义vector的时候规定其sort√

    • 路径问题，所以跟深度有关，使用DFS遍历。剪枝限制条件就是给定的常数S，对于每个结点而言，如果到此的路径和sum分为三种情况。

    • sum>S：此时return，该路径不可能输出。sum<S：此时继续，如果是叶子结点，则该路径不可能输出。sum=S：如果是叶子结点则保存继续；如果不是则return，该路径不可能输出。

    • 保存的路径可以用path数组或者vector保存。

#include<cstdio>
#include<vector>
#include<algorithm>
using namespace std;
const int MAXN = 110;
struct node{
    int weight;
    vector<int> child;
}Node[MAXN];

bool cmp(int a, int b){
    return Node[a].weight > Node[b].weigth;
}

int n , m ,s;
int path[MAXN];

void DFS(int index, int numNode, int sum){
    if(sum > s) return;
    if(sum == s){
        if(Node[index].child.size() != 0) return;
        for(int i = 0; i < numNode; i++){
            printf("%d",Node[path[i]].weight);
            if(i < numNode - 1) printf(" ");
            else printf("\n");
        }
        return ;
    }   
    for(int i = ; i < Node[index].child.size(); i++){
        int child = Node[index].child[i];
        path[numNode] = child;
        DFS(child, numNode + 1, sum + Node[child].weight);
    }
}

int main(){
    scanf("%d%d%d",&n,&m,&S);
    for(int i = 0; i < n; i++)  scanf("%d",&Node[i].weight);
    int id,k,child;
    for(int i = 0; i < m; i++){
        scanf("%d%d",&id,&k);
        for(int j = 0 ; j < k; j++){
            scanf("%d",&child);
            Node[id].child.push_back(child);
        }
        sort(Node[id].child.begin(),Node[id].child.end(),cmp);
    }
    paht[0] = 0;
    DFS(0,1,Node[0].weight);
    return 0;
}

9.4 二叉查找树（BST）

9.4.1 二叉查找树的定义

• 二叉查找树（Binary Search Tree BST）是一种特殊二叉树，又称为排序二叉树，二叉搜索树，二叉排序树。

• BST递归定义：

  • 要么是二叉查找树是一棵空树

  • 要么二叉查找树是根结点，左子树，右子树，其左子树右子树都是二叉查找树。

  • 左子树所有结点数据域小于等于根结点数据域，右子树结点数据域均大于根结点数据域

9.4.2 二叉查找树的基本操作

• 查找、插入、建树、删除。算法过程都是由一般二叉树改造而来。

• 二叉查找树的查找操作：

  • 由于二叉查找树的性质，决定进行递归遍历时，只会选择其中一棵子树进行查找，因此查找过程就是根结点到查找结点的一条路径。最坏O(h)，h为树高度。

  • 类似二分性质，比较值往左往右查找 - 查找结点为null时查找失败

void search(node* root, int x){
    if(root == null){
        printf("search failed\n");
        return;
    }
    if(x == root->data){
        printf("%d",root->data);
    }
    else if(x < root->data) search(root->lchild, x);
    else search(root->rchild, x);
}

• 二叉查找树的插入操作：
  • 插入 = 查找失败 + 新建结点

void insert(node* &root, int x){
    if(root == NULL){
        root = newNode(x);
        return;
    }
    if(x == root->data){
        return;     // 已经存在不需要插入
    }
    else if(x < root->data) search(root->lchild, x);
    else search(root->rchild, x);
}

• 二叉查找树的建立操作：
  • 相同一组数字，不同的插入顺序，最后生成的二叉查找树也可能不相同

node* Create(int data[], int n){
    node* root = null;
    for(int i = 0; i < n; i++)  insert(root, data[i]);
    return root;
}

• 二叉查找树的删除操作：

  • 一般有两种常见做法，复杂度都是O(h)，此处主要介绍简单易写的一种（另一种见代码优化）。

  • 在二叉查找树中，比结点权值小的最大结点称为前驱，权重大的最小结点称为后继。结点前驱是在该结点左子树的最右结点（在左子树下的不断rchild直至为null），结点后继是在该结点右子树的最左结点（在右子树下的不断lchild直至为null）。

  • 删除某个结点，可以将该结点的前驱 / 后继移动到删除结点位置，调整成新的二叉查找树。

  • 假设决定用结点N的前驱P来替换N（有前驱就用前驱，没前驱就用后继），那么问题又转化递归为子问题：在N的左子树中删除结点P - 直至递归到一个叶子结点，便可以直接将他删除不需要替代。

  • 代码优化：假设欲删除结点root的前驱结点next，肯定是其父结点S的右子树根结点，并且next没有右孩子；可以直接将next的左子树挂到S上作为其右子树，这样就不用递归优化代码。 - 利用后继结点也是同理。

  • 总是优先删除前驱或者后继结点容易导致树的左右子树高度不平衡，使得退化成一条链，解决方法可以每次交替删除，也可以记录子树高度，优先删除高度较高的一边。

// 寻找树中的最大权值结点 - 利用找到前驱结点
node* findMax(node* root){
    while(root->rchild != NULL) root = root->rchild;
    return root;
}

//寻找树中的最小权值结点 - 利用找到后继结点
node* findMin(node* root){
    while(root->lchild != NULL) root = root->lchild;
    return root;
}

// 删除树中权值为x的结点并作调整
void deleteNode(node* &root, int x){
    if(root == null) return;
    if(root->data > x)  deleteNode(root->lchild, x);
    else if(root->data < x) deleteNode(root->rchild, x);
    else{
        if(root->lchild == null && root->rchild == null)    root = null;
        else if(root->rchild != null){
            node* pre = findMax(root->lchild);
            root->data = pre ->data;
            deleteNode(root->lchild, pre->data);
        }
        else {
            node* next = findMin(root->rchild);
            root->data = next ->data;
            deleteNode(root->rchild, next->data);
        }
    }
}

9.4.3 二叉查找树的性质

• 对二叉查找树进行中序遍历，遍历序列是递增有序的。

• 如果合理调整二叉查找树的形态，使得每个节点都尽量有两个子结点，这样会使得树的高度降低，大概在log(N)级别 - 这样的树就是平衡二叉树（AVL）

• 二叉查找树的镜像树：就是左子树>根结点>右子树，中序遍历出来的是递减序列。

  • 对镜像树的先序遍历就是原树的先序遍历+把左右访问顺序交换

9.5 平衡二叉树（AVL树）

9.5.1 平衡二叉树的定义

• 对二叉查找树的结构进行调整，使得树的高度在每次插入元素后仍然能保持O(logN)级别，这样能让查询操作仍然是O(logN)的时间复杂度。 - 特殊的二叉查找树，在基础上添加了平衡的要求

  • 平衡：对AVL树任意结点而言，左子树和右子树的高度差的绝对值不超过1，高度差称为该结点的平衡因子。

  • 由于需要对每个结点都得到平衡因子，所以需要在结点结构加入变量height，记录当前结点为根结点的子树高度。

struct node{
    int v, height;
    node *lchild, *rchild;
};

node* newNode(int v){
    node* Node = new node;
    Node->v = v;
    Node->height = 1;
    Node->lchild = Node->rchild = null;
    return Node;
}

int getHeigth(node* root){
    if(root == null) return 0;
    return root->height;
}

int getBalanceFactor(node* root){
    return getHeigth(root->lchild) - getHeight(root->rchild);
}

void updateHeight(node* root){
    root->height = max(getHeight(root->lchild),getHeight(root->rchild))+1;
}

9.5.2 平衡二叉树的基本操作

• 基本操作有：查找，插入，建树（删除比较复杂本节没有介绍）

• AVL树的查找操作：

  • 查找做法与二叉查找树一致，左小右大二分思想，时间复杂度O(logN)

  • 与二叉查找树代码完全相同

void search(node* root, int x){
    if(root == null){
        printf("search failed\n");
        return;
    }
    if(x == root->data){
        printf("%d",root->data);
    }
    else if(x < root->data) search(root->lchild, x);
    else search(root->rchild, x);
}

• AVL树的插入操作：

  • 二叉查找树的左旋：将右子树根结点B调整为根结点A，使得（左边高度+1，右边高度-1） - 适用于左边高度小于右边高度，平衡因子失衡的情况

    • eg. ⚪-根-⚪-⚪-⚪，对此失衡采用左旋操作调整为平衡状态

    • 步骤：右子树根结点B的左子树变成根结点A的右子树，根结点A变成右子树根结点B的左子树，B成为新的根结点。 - 相当于AB地位交换，子树交换。

  • 二叉查找树的右旋：与左旋步骤类似，针对左边高度大于右边高度，平衡因子失衡情况

    • eg. ⚪-⚪-⚪-根-⚪

    • 步骤：左子树根结点C的右子树变成根结点A的左子树，根结点A变成左子树根结点C的右子树，C成为新的根结点。 - 相当于AC地位交换，子树交换。

  • AVL树插入结点后，一定会导致结点的平衡因子变化，可能导致失衡，平衡因子绝对值大于1（只可能是2 / -2，因为插入前是正常的平衡因子，插入后最多+/-1）。只需要把最靠近插入结点的失衡结点调整到正常，路径上的所有结点就都会平衡。

    • 假设A是最靠近的失衡节点。平衡因子=2，即左边高。根据左子树=1/-1分为LL型和LR型；平衡因子=-2，即右边高，根据右子树=1/-1分为RL型和RR型。（如果A不是最靠近的，那么它子树的平衡因子不为+-1）

    • LL型：A结点平衡因子=2，左子树根结点平衡因子=1，直接对root进行右旋

    • LR型：A结点平衡因子=2，左子树根结点平衡因子=-1，先对左子树根结点进行左旋，再对root进行右旋

    • RL型：A结点平衡因子=-2，右子树根结点平衡因子=1，先对右子树根结点进行右旋，再对root进行左旋

    • RR型：A结点平衡因子=-2，右子树根结点平衡因子=-1，直接对root进行左旋。

// 左旋（Left Rotation）
void L(node* &root){
    node* temp = root->rchild;
    root->rchild = temp->lchild;
    temp->lchild = root;
    updateHeight(root);
    updateHeight(temp);
    root = temp;
}

// 右旋（Right Rotation）
void R(node* &root){
    node* temp = root->lchild;
    root->lchild = temp->rchild;
    temp->rchild = root;
    updateHeight(root);
    updateHeight(temp);
    root = temp;
}

// AVL树插入操作
void insert(node* &root, int v){
    if(root == null){
        root = newNode(v);
        return;
    }
    if(v < root->v){
        insert(root->lchild,v);
        updateHeight(root);
        if(gerBalanceFactor(root) == 2)
            if(getBalanceFactor(root->lchild) == 1) R(root);
            else if(getBalanceFactor(root->lchild) == -1){
                L(root->lchild);
                R(root);
            }
    }else{
        insert(root->rchild, v);
        updateHeight(root);
        if(gerBalanceFactor(root) == -2)
            if(getBalanceFactor(root->rchild) == -1) L(root);
            else if(getBalanceFactor(root->rchild) == 1){
                R(root->rchild);
                L(root);
            }
    }
}

• AVL树的建立操作：

node*   Create(int data[], int n){
    node* root = null;
    for(int i = 0; i < n; i++)  insert(root, data[i]);
    return root;
}

9.6 并查集

9.6.1 并查集的定义

• 并查集是一种维护集合的数据结构，支持两种操作：合并 - 合并两个集合，查找 - 判断两个元素是否属于同一个集合

  • 并查集产生的每一个集合都是一棵树

• 在本书中简单并查集直接用了一个数组来实现：int father[N];

  • father[i] = k，表示元素i的父结点是k，k也是这个集合中的元素，i和k同属一个集合

  • father[i] = i，表示元素i是该集合的根结点，对同一个集合而言只存在一个根结点，作为该集合的标识

9.6.2 并查集的基本操作

• 初始化：一开始每个结点都指向自己，每个结点都单独作为一个集合

for(int i = 1; i <= N; i++){
    father[i] = i;
}

• 查找：对给定结点递归/循环查找直至根结点（father[i] == i）

// 循环
int findFather(int x){
    while(x != father[x])   x = father[x];
    return x;
}

// 递归
int findFather(int x){
    if(x == father[x])  return x;
    else return findFather(father[x]);
}

• 合并：将两个集合合并成一个集合。一般是给出两个元素，要求把两个元素所属集合合并。

  • 先判断是否属于同一集合；使用查找函数判断是否指向同一根结点

  • 如果不属于同一集合，将集合元素个数少的根结点指向元素个数多的根结点。合并完成

void Union(int a, int b){
    int faA = findFather(a);
    int faB = findFather(b);
    if(faA != faB)  father[faA] = faB;
}

9.6.3 路径压缩

• 上述并查集的查找函数没有经过优化，需要一直一直往上遍历查找；实际上应该在进行一次长串低效率查找后，就应该能对集合树结构进行优化
  • 查找串上的所有经过结点都直接指向根结点，这样后续的复杂度降为O(1)

// 路径压缩查找函数 - 非递归
int findFather(int x){
    int a = x;
    while(x != father[x])   x= father[x];
    while(a != father[a]){
        int z = a;
        a = father[a];
        father[z] = x;
    }
    return x;
}

// 路径压缩查找函数 - 递归
int findFather(int v){
    if(v == father[v])  return v;
    else{
        int F = finFather(father[v]);
        father[v] = F;
        return F;
    }
}

9.7 堆

9.7.1 堆的定义与基本操作

• 堆是一棵完全二叉树

  • 大根堆（大顶堆）：父亲结点值大于等于孩子结点值，根结点为最大值

  • 小根堆（小顶堆）：父亲结点值小于等于孩子结点值，根结点为最小值

  • 堆结构一般用于优先队列的实现，而要用到堆结构时可以使用优先队列实现算法，默认使用大根堆。

  • 对于完全二叉树而言用数组存储实现较为简单，左孩子为2i，右孩子为2i+1，从下标1开始存储

• 大根堆建堆操作 - 全部放到堆内，只需要进行[n/2]次向下调整即可（因为[n/2]个非叶子结点），调整时间复杂度O(logN)，建堆时间复杂度O(N)

  • 遍历结点，各结点与左右孩子比较，如果没有孩子或者结点值最大则跳过，否则与左右孩子中值最大的交换结点，循环往下比较直至到叶子结点。

const int maxn = 100;
int heap[maxn], n = 10;     // n为堆内元素个数

// 堆[low,high]范围内进行向下调整，low为调整结点下标，high为最后元素下标
void downAdjust(int low, int high){
    int i = low, j = i * 2;
    while(j <= high){
        if(j+1<=high && heap[j+1] > heap[j])    j++;
        if(heap[j] > heap[i]){
            swap(heap[j],heap[i]);
            i = j ;
            j = i * 2;
        }else break;
    }
}

// 建堆
void createHeap(){
    for(int i = n / 2; i >= 1; i--) downAdjust(i,n);
}

• 大根堆删除堆顶元素操作：
  • 堆内最后一个元素覆盖堆顶元素，再堆根结点进行一次向下调整即可，时间复杂度O(logN)

void deleteTop(){
    heap[1] = heap[n--];
    downAdjust(1,n)
}

• 大根堆添加元素操作：
  • 将新添加元素至最后下标处，再对其进行向上调整，与向下调整相反，总是将结点与其父结点比较，如果是比之大则交换继续，直至到根结点或者比父结点小就停止。时间复杂度O(logN)

// [low,high]范围内进行向上调整，一般low=1，high为调整结点下标
void upAdjust(int low, int high){
    int i = high, j = i / 2; 
    while(j >= low){
        if(heap[j] < heap[i]){
            swap(heap[j], heap[i]);
            i = j;
            j = i / 2;
        } else break;
    }
}

// 添加元素x
void insert(int x){
    heap[++n] = x;
    upAdjust(1,n);
}

9.7.2 堆排序

• 堆排序直观思路：取出堆顶元素，进行删除元素操作，重复取出直至堆空。

  • 具体实现时，为节省空间，可以倒着遍历数组，将堆顶元素与遍历i下标元素交换，接着在[1,i-1]范围内对堆顶元素进行一次向下调整。

  • 到最后整个数组就是从小到大的递增序列。

void heapSort(){
    createHeap();
    for(int i = n; i > 1; i--){
        swap(heap[i], heap[1]);
        downAdjust(1, i-1);
    }
}

9.8 哈夫曼树

9.8.1 哈夫曼树

• 经典的合并果子问题 - 类似牛客网算法的分金条问题

  • 每个最小单位都是叶子结点，单位值作为结点权值，叶子结点到根结点经过的边数叫做其路径长度，乘上叶子结点权值为叶子结点的带权路径长度，而这类问题实际上都是求最小树的带权路径长度（WeightedPathLength of Tree WPL），即所有叶子结点的带权路径长度和。

  • 转化为：已知n个数，寻找一棵树，使得n个数为树的所有叶子结点且其带权路径长度最小。 - 该树称之为哈夫曼树（又称最优二叉树），对同一组叶子结点而言，哈夫曼树可以不唯一，但是WPL长度唯一（相等结点交换左右结点位置就不唯一了）。

  • 哈夫曼树构建思想：反复选择最小两个元素，左小右大合并，直到只剩下一个元素。一般使用优先队列（小根堆）来实现算法，即取出两个数相加再压回堆中重复操作。

#include<cstdio>
#include<queue>
using namespace std;

priority_queue<long long, vector<long long>, greater<long long>> q;

int main(){
    int n;
    long long temp, x, y, ans = 0;
    scanf("%d", &n);
    for(int i = 0; i < n; i++){
        scanf("%lld", &temp);
        q.push(temp);
    }
    while(q.size() > 1){
        x = q.top();
        q.pop();
        y = q.top();
        q.pop();
        q.push(x+y)
        ans += x+y;
    }
    printf("%lld\n", ans);
    return 0;
}

9.8.2 哈夫曼编码

• 二叉树左分支为0，右分支为1；对任何一个非叶子结点其编号一定是某叶子结点前缀；对任何叶子结点其编号一定不会是前缀

  • 前缀编码：任何一个字符的编码都不会是另一个字符编码的前缀（存在意义在于不产生混淆让解码正常进行） - 将字符作为二叉树的叶子结点进行01编码。

  • 编码01串后的长度实际上就是树的带权路径长度 - 每个字符出现出现的频率或者次数作为叶子结点权值

  • 由哈夫曼树产生的编码称为哈夫曼编码 - 是能使给定字符串编码成01串后长度最短的前缀编码。对应的哈夫曼编码可能不唯一，但是编码最短长度唯一。

  • 哈夫曼编码是针对已经确定的字符串来讨论的，只有确定的字符串才能根据其中各字符的出现次数来建立哈夫曼树。

第十章 提高篇(4) - 图算法专题

10.1 图的定义和相关术语

• 图由顶点(Vertex)和边(Edge)组成，分为有向图和无向图，有向图需要指明方向，无向图都是双向的。

  • 有时候可以把无向图视为双向的有向图。

• 顶点的度是指和该顶点相连边的条数。对有向图而言，出边条数称为出度，入边条数称为入度。

• 顶点和边都可有一定属性，量化的属性称为权值，分别为点权和边权，具体含义视题目而定。

10.2 图的存储

• 图的存储方式一般分为两种，一种为邻接矩阵，一种为邻接表。也有另一种化为类图（边+结点）的存储方式，需要对邻接矩阵进行转化。

10.2.1 邻接矩阵

• 使用二维数组G[N][N]表示图的顶点标号，如果G[i][j]为1则表示顶点i与j之间有边；如果G[i][j]为0则说明不存在边。这个二维数组被称为邻接矩阵。

• 如果是带权图，则G[i][j]存放边权值，对不存在的边可以设为0，-1，或者很大的值。

• 邻接矩阵虽然比较容易写，但是需要开一个二维数组，如果顶点数目太多就可能会超过题目限制的内存（一般不超过1000）

• 邻接矩阵也有另一种可以表示范围更大的存储方式，相对第一种更省内存：matrix[n][0,1,2]。 - n个结点，其中一维列表：[边权,起点,终点]，这样占用空间就跟边数相关（前者更点数相关，并且是平方倍）。

10.2.2 邻接表

• 邻接表：每个顶点对应一个以该点为起点的出边链表，N个顶点对应N条链表，记为Adj[N]。其中每个链表结点存放一条边的权值以及终点信息。 - 其中链表使用vector来实现，vector可以放int实现无权图，放struct实现有权图。

10.2.3 类图（补充）

• 类图 - 由二维列表生成类图

  • Node点结构：value，入度in，出度out，邻接节点Arraylist（出度节点），邻接边Arraylist（出度边）。

  • Edge边结构：权重，from，to。

  + Graph图结构：点Arraylist，边Arraylist

  • 转化成类图后方便图相关问题的解决 - 点集边集等，所有关于图的算法都可以用类图结构方便

• 算法实现（Java）

// 点
public class Node {
	public int value;
	public int in;
	public int out;
	public ArrayList<Node> nexts;
	public ArrayList<Edge> edges;

	public Node(int value) {
		this.value = value;
		in = 0;
		out = 0;
		nexts = new ArrayList<>();
		edges = new ArrayList<>();
	}
}

//边
public class Edge {
	public int weight;
	public Node from;
	public Node to;

	public Edge(int weight, Node from, Node to) {
		this.weight = weight;
		this.from = from;
		this.to = to;
	}
}

//图
public class Graph {
	public HashMap<Integer,Node> nodes;
	public HashSet<Edge> edges;

	public Graph() {
		nodes = new HashMap<>();
		edges = new HashSet<>();
	}
}

// 二维列表构造类图
public static Graph createGraph(Integer[][] matrix) {
		Graph graph = new Graph();
		for (int i = 0; i < matrix.length; i++) {       // 此处的二维列表与G[i][j]不同，是G[n][0,1,2]
			Integer from = matrix[i][0];
			Integer to = matrix[i][1];
			Integer weight = matrix[i][2];
			if (!graph.nodes.containsKey(from)) {
				graph.nodes.put(from, new Node(from));
			}
			if (!graph.nodes.containsKey(to)) {
				graph.nodes.put(to, new Node(to));
			}
			Node fromNode = graph.nodes.get(from);
			Node toNode = graph.nodes.get(to);
			Edge newEdge = new Edge(weight, fromNode, toNode);
			fromNode.nexts.add(toNode);
			fromNode.out++;
			toNode.in++;
			fromNode.edges.add(newEdge);
			graph.edges.add(newEdge);
		}
		return graph;
	}

• 其他更多相关类图的算法实现看博客另一篇文章：算法<初级> - 第四章 前缀树、图等相关问题（完结）

10.3 图的遍历

• 图的遍历是指对图的所有顶点按一定顺序进行访问：DFS深搜 & BFS广搜

10.3.1 DFS遍历图

• 连通图：如果图中任何了两个顶点都相通（相互到达）则称图为连通图；其中连通图称为连通分量，一个图可能有多个连通分量。

• 强连通图：如果图中任何了两个顶点都各有有向路径通达则称图为强连通图；其中强连通图称为强连通分量，一个图可能有多个强连通分量。

• DFS遍历图的基本思路：将经过的顶点设置为已访问，在下次遍历/递归碰到顶点的时候就不再去处理，直至整个图的顶点都标记为已访问。

  • 如果不使用递归，而是非递归准备个栈：初始顶点，入栈+set+打印，循环 - 弹栈出度顶点依次判断入栈set打印 / 无出度节点未注册则弹栈。直至栈变空

// 伪代码
DFS(u){     // 访问顶点u
    vis[u] = true;      // 用数组标记 - 可以用一个set集合来作标记
    for(从u出发能到达的所有顶点v)      // 枚举邻接顶点
        if vis[v] == false      // 如果v未被访问
            DFS(v);     //递归访问v - 非递归版本则用栈来存储
}

DFSTrave(G){        // 遍历图G
    for(G的所有顶点u)
        if vis[u] == false
            DFS(u);
}

// 邻接矩阵版DFS
const int MAXV = 1000;
const int INF = 100000000;

int n, G[MAXV][MAXV];
bool vis[MAXV] = {false};

void DFS(int u, int depth){
    vis[u] = true;
    for(int v = 0; v < n; v++){
        if(vis[v] == false && G[u][v] != INF){
            DFS(v, depth+1);
        }
    }
}

void DFSTrave(){    // 遍历图G
    for(int u = 0; u < n; u++){
        if(vis[u] == false) DFS(u,1);
    }
}

//邻接表版DFS
const int MAXV = 1000;
const int INF = 100000000;
vector<int> Adj[MAXV];
int n;
bool vis[MAXV] = {false};

void DFS(int u, int depth){
    vis[u] = true;
    for(int i = 0; i < Adj[u].size(); i++){
        int v = Adj[u][i];
        if(vis[v] == false) DFS(v,depth+1);
    }
}

void DFSTrave(){
    for(int u = 0; u < n; u++)
        if(vis[u] == false) DFS(u,1);
}

// 类图非递归DFS - Java实现
	public static void dfs(Node node) {
		if (node == null) {
			return;
		}
		Stack<Node> stack = new Stack<>();
		HashSet<Node> set = new HashSet<>();
		stack.add(node);        // 入栈
		set.add(node);      // set
		System.out.println(node.value);     //打印
		while (!stack.isEmpty()) {          // 栈空结束
			Node cur = stack.pop();     // 弹栈
			for (Node next : cur.nexts) {   // 依次判断入栈入set打印
				if (!set.contains(next)) {
					stack.push(cur);
					stack.push(next);
					set.add(next);
					System.out.println(next.value);
					break;
				}
			}
		}
	}

10.3.2 BFS遍历图

• 和之前的DFS一样，都是对单个连通块进行遍历操作。基本思想：
  • 使用队列实现，初始顶点入队列和set，(弹队列打印，所有出度节点判断入队列set)。直至队列变空

BFS(u){
    queue q;
    将u入队;
    inq[u] = true;      // 标记set
    while(q非空){
        取出q的队首元素u进行访问;
        for(从u出发可达的所有顶点v)
            if(inq[v] == false){
                将v入队;
                inq[v] = true;
            }
    }
}

BFSTrave(G){
    for(G的所有顶点u)
        if(inq[u] == false) BFS(u);
}

// 邻接矩阵版BFS
int n, G[MAXV][MAXV];
bool inq[MAXV] = {false};

void BFS(int u){
    queue<int> q;
    q.push(u);
    inq[u] = true;
    while(!q.empty()){
        int u = q.front();
        q.pop();
        for(int v = 0; v < b; v++){
            if(inq[v] == false && G[u][v] != INF){
                q.push(v);
                inq[v] = true;
            }
        }
    }
}

void BFSTrave(){
    for(int u = 0; u < n; u++)
        if(inq[u] == false) BFS(q);
}

// 邻接表版BFS
vector<int> Adj[MAXV];
int n;
bool inq[MAXV] = {false};

void BFS(int u){
    queue<int> q;
    q.push(u);
    inq[u] = true;
    while(!q.empty()){
        int u = q.front();
        q.pop();
        for(int i = 0; i < Adj[u].size(); i++){
            int v = Adj[u][i];
            if(inq[v] == false){
                q.push(v);
                inq[v] = true;
            }
        }
    }
}

void BFSTrave(){
    for(int u = 0; u <n; u++)
        if(inq[u] == false) BFS(q);
}

// 考虑层号并且用顶点用node属性 - BFS进行稍作修改
void BFS(int s){        // s为起始顶点
    queue<node> q;
    Node start;
    start.v = s;
    start.layer = 0;
    q.push(start);
    inq[start.v] = true;
    while(!q.empty()){
        Node topNode = q.front();
        q.pop();
        int u = topNode.v;
        for(int i = 0; i < Adj[u].size(); i++){
            Node next = Adj[u][i];
            next.layer = topNode.layer+1;
            if(inq[next.v] == false){
                q.push(next);
                inq[next.v] = true;
            }
        }
    }
}

// 类图BFS - Java实现
	public static void bfs(Node node) {     // 传参图中的起始节点
		if (node == null) {
			return;
		}
		Queue<Node> queue = new LinkedList<>();
		HashSet<Node> map = new HashSet<>();
		queue.add(node);
		map.add(node);
		while (!queue.isEmpty()) {
			Node cur = queue.poll();
			System.out.println(cur.value);
			for (Node next : cur.nexts) {
				if (!map.contains(next)) {
					map.add(next);
					queue.add(next);
				}
			}
		}
	}

10.4 最短路径

• 给定图G(V,E)，求一条从起点到终点的路径，使得这条路上经过的所有边的边权之和最小

• 解决最短路径的常用算法有：Dijkstra算法，Bellman-Ford算法，Floyd算法，，SPFA算法。

10.4.1 Dijkstra算法

• Dijkstra迪杰斯特拉算法：解决单源最短路问题，且没有负数权值边，即给定图G和起点s，通过算法得到s到达其他每个顶点的最短距离

  • 如果边权出现负数情况，Dijkstra算法可能出错，最好使用SPFA算法

• 基本思想：

  • 对图G(V,E)设置集合set存放已被访问顶点，然后每次从集合V-set（即未被访问顶点）中选择与起点s最短距离最小的一个顶点（记为u），访问并加入set，令u为中介点，优化起点s与u的所有邻接顶点的最短距离（div[s,k] = min(div[s,k],div[s,u]+w[u,k])），重复操作直至set包含所有顶点。

  • div表示s到各个顶点的最短距离，w表示各条边的边权重

  • 实现方法一：经典Dijkstra，遍历选择最近节点，遍历更新邻接节点距离，加入set注册最近节点，循环直至没有出度节点。（就是上述思想）

    • 邻接矩阵版：时间复杂度O(V²)

    • 邻接表版：时间复杂度O(V²+E)

  • 实现方法二：使用堆结构优化Dijkstra算法，用优先队列小根堆去优化选择最近节点这步降低复杂度，循环直至没有出度节点。（实现较为复杂点，在牛客网算法的笔记中有写）

    • 时间复杂度：O(VlogV)

// Dijkstra伪代码 G为图 数组d为源点到各点的最短路径长 s为起点
Dijkstra(G, d[], s){
	初始化;
	for(循环n次){
		u = 使d[u]最小的还未被访问的顶点的标号;	//经典遍历，优化用堆
		记u已被访问;
		for(从u出发能到达的所有顶点v)
			if(v未被访问&&以u为中介点使s到顶点v的最短距离d[v]更优)
				优化d[v];
	}
}	

const int MAXV = 1000;
const int INF = 1000000;

// 邻接矩阵Dijkstra
int n, G[MAXV][MAXV];
int d[MAXV];
bool vis[MAXV] = {false};

void Dijkstra(int s){
	fill(d, d+MAXV, INF);
	d[s] = 0;
	for(int i = 0; i < n; i++){		// 遍历所有顶点
		int u = -1, MIN = INF;
		for(int j = 0; j < n; j++)		// 找到未访问顶点中d[]最小的
			if(vis[j] == false && d[j] < MIN){
				u = j;
				MIN = d[j];
			}
		// 找不到小于INF的d[u]，说明剩下的顶点与起点s不连通
		if(u == -1 ) return;
		vis[u] = true;
		for(int v = 0; v < n; v++){		// 优化邻接顶点
			if(vis[v] == false && G[u][v] != INF && d[u] + G[u][v] < d[v])
				d[v] = d[u] + G[u][v];
		}
	}
}

// 邻接表版Dijkstra
struck Node{
	int v, dis;
};
Vector<Node> Adij[MAXV];
int n;
int d[MAXV];
bool vis[MAXV] = {false};

void Dijkstra(int s){
	fill(d, d+ MAXV, INF);
	d[s] = 0;
	for(int i = 0; i < n; i++){
		int u = -1, mIN = INF;
		for9int j = 0; j < n; j++){
			if(vis[j] == false && d[j] < MIN){
				u = j;
				MIN = d[j];
			}
		}
		if( u == -1) return;
		vis[u] = true;
		for(int j = 0; j < Adj[u].size();j++){
			int v = Adj[u][j].v;
			if(vis[v] == false && d[u] + Adj[u][j].dis < d[v]){
				d[v] = d[u] + Adj[u][j].dis;
			}
		}
	}
}

• 上述为最短距离的求解，而最短距离路径的求解即在优化d[]数组处记录：

  • 若u是中介点，更新了s到v的最短距离d[v]

  • 设置一个pre[]数组来记录s到某点最短路径的前一个结点 - 在优化d[]后记录pre[v] = u，最后只需要用一个递归或者while循环+栈来根据pre数组打印最短路径即可

//递归
void DFS(int s, int v){
	if(v == s){
		printf("%d\n",s);
		return;
	}
	DFS(s,pre[v]);
	printf("%d\n",v);
}

• 除了会求最短距离，最短距离路径之外，题目还可能会出第二尺度（第一尺度是距离）：即有多条最短距离路径，选出最优第二尺度路径。

  • 常见的第二尺度：点权（eg. 每个城市所能收集的物资），边权（eg. 每条路的花费），一共有多少条（不算第二尺度）

  • 对此只需要添加一个数组来存放新增的边权/点权/条数，再修改优化d[]步骤即可

// 新增边权
for(int v= 0; v < n; v++){
	if(vis[v] == false && G[u][v] != INF){
		if(d[v] = d[u] + G[u][v] < d[v]){	// d[v]优化
			d[v] = d[u] + G[u][v];
			c[v] = c[u] + cost[u][v]; 	// c[]是边权数组
		}  esle if(d[u] + G[u][v] == d[v] && c[u] + cost[u][v] < c[u]){		// 第二尺度优化
			c[v] = c[u] + cost[u][v];	
		}
	}
}

// 新增点权
for(int v= 0; v < n; v++){
	if(vis[v] == false && G[u][v] != INF){
		if(d[v] = d[u] + G[u][v] < d[v]){	// d[v]优化
			d[v] = d[u] + G[u][v];
			w[v] = w[u] + weight[u][v]; 	// w[]是边权数组
		}  esle if(d[u] + G[u][v] == d[v] && w[u] + weight[u][v] < w[u]){		// 第二尺度优化
			w[v] = w[u] + weight[u][v];	
		}
	}
}

// 最短路径总共有多少条
for(int v= 0; v < n; v++){
	if(vis[v] == false && G[u][v] != INF){
		if(d[v] = d[u] + G[u][v] < d[v]){	// d[v]优化
			d[v] = d[u] + G[u][v];
			num[v] = num[u];
		}  esle if(d[u] + G[u][v] == d[v]){		// 有其他最短路径
			num[v] += num[u];	
		}
	}
}

10.4.2 Bellman-Ford 算法和 SPFA 算法

• Bellman-Ford（BF）算法：可解决单源最短路径问题，也可以处理有负权边情况

  • SPFA算法是BF算法的优化版本

• 环：从某顶点出发，经过若干个不同的顶点之后可回到该顶点

  • 根据环内边的权值之和正负，分为零环（1,-2,1），正环（1,1,1），负环（-1,-1,1）。

  • 正环和零环不会影响最短路的求解，但是如果有负环，且从源点可达，则会影响最短路径的求解（如果不可达也不会影响最短路求解） - 可以无限走负环使得代价越来越小直至负无穷。

• BF算法设置一个数组d[]存放源点到各个顶点的最短距离，同时返回一个bool值，判断图内是否有从源点可达的负环。

  • 对图中边进行V-1轮操作，每轮遍历所有边E（因为最短路径层数/顶点个数不会超过V个）

  • 对每条边u->v，如果u中介点使d[v]优化，则更新。时间复杂度O(VE)（路径优化在BF算法里面称为松弛）

  • 经过以上优化后O(VE)后，如果没有源点可达负环，则d[]数组已经最优，如果仍可以被松弛（被优化），则说明有负环返回false

// 伪代码
for(i = 0; i < n - 1; i++){
	for(each egde u->v){
		if(d[u] + length[u->v] < d[v])	d[v] = d[u] + length[u->v];
	}
}

// 判断负环
for(each egde u->v){
		if(d[u] + length[u->v] < d[v])	return false;
}
return true;

• BF算法由于要遍历所有边，显然用邻接表会方便，如果使用邻接矩阵则需要去遍历V²找边（用另一种邻接矩阵实现也方便）

// 邻接表版BF算法实现
struct Node{
	int v, dis;
};
vector<Node> Adj[MAXV];
int n;
int d[MAXV];

bool Bellman(int s){
	fill(d, d+ MAXV, INF);
	d[s] = 0;
	for(int i = 0; i < n - 1; i++){
		for(int u = 0; u < n; u++)
			for(int j = 0; j < Adj[u].size();j++){
				int v= Adj[u][j].v;
				int dis = Adj[u][j].dis;
				if(d[u] + dis < d[v])
					d[v] = d[u] + dis;
			}
	}
}

// 判断负环
for(int u = 0; u < n; u++)
    for(int j = 0; j < Adj[u].size();j++){
        int v= Adj[u][j].v;
        int dis = Adj[u][j].dis;
        if(d[u] + dis < d[v])
        	return false;
    }
return ture;

• 以上代码可以进行剪枝：在某一轮操作时，如果发现所有边都没有被松弛，则说明d[]数组已经达到最优值。

• 最短路径求解和多尺度做法与Dijkstra算法一样，都是在松弛（优化）阶段修改部分代码即可

  • 唯一需要注意的是统计最短路径条数的做法：BF算法会多次访问曾经访问过的顶点，需要设置记录前驱的数组set pre[]。每个数组记录前驱集合，如果遇到和已有最短路径相同的路径时，则更新过的最短路条数--。

• SPFA算法：BF算法每轮（共V-1轮）会操作所有边，会产生大量无意义操作 - 改良：只有当某个顶点u的d[u]值改变时，从它出发的边邻接点v的d[v]值才可能改变。

  • SPFA实现：使用队列，首先将队首顶点u取出，然后对u出发的所有边进行松弛（判断是否更新），如果更新则把相应的v加入队列中（已存在则不管）。这样操作直至队列为空或者某个顶点入队次数超过V-1（说明图中有源点可达的负环）

  • 时间复杂度O(kE)，k是常数，通常情况下不超过2。效率经常优于堆优化的Dijkstra算法，但如果图中有可达负环则时间复杂度会退化为O(VE)。

  • 如果负环从源点不可达，需要添加一个辅助顶点C，并且添加一条从源点到达C得有向边以及V-1条从C到达除源点外各顶点得有向边才能判断负环存在与否

// 伪代码
queue<int> Q;
源点s入队;
while(队列非空){
	取出队首元素u;
	for(u的所有邻接边u->v){
		if(d[u] + dis < d[v]){
			d[v] = d[u] + dis;
			if(v当前不在队列){
				v入队;
				if(v入队次数大于n-1)	// 说明有可达负环
					return;
			}
		}
	}
}

// 邻接表版SPFA
vector<Node> Adj[MAXV];
int n , d[MAXV], num[MAXV];
bool inq[MAXV];

bool SPFA(int s){
	// 初始化
	memset(inq, false, sizeof(inq);
	memset(num, 0 , sizeof(num));)
	fill(d, d + MAXV, INF);
	queue<int > Q;
	Q.push(s);
	inq[s] = true;
	num[s]++;
	d[s] = 0;
	while(!Q.empty()){
		int u = false;
		for(int j = 0; j < Adj[u].size(); j++){
			int v = Adj[u][j].v;
			int dis = Adj[u][j].dis;
			if(d[u] + dis < d[v]){
				d[v] = d[u] + dis;
				if(!inq[v]){
					Q.push(v)
					inq[v] = true;
					num[v]++;
					if(num[v] >= n) return false;	//有可达负环
				}
			}
		}
	}
	return true;
}

• SPFA改进：可以将队列替换成优先队列加快速度，或者替换成双端队列使用SLF优化 / LLL优化可以提高效率50%以上。除此之外，上述代码是SPFA的BFS版本（即用队列），也可以将队列替换成栈，实现DFS版本的SPFA，该种方法对判断负环有奇效。

  • spfa的SLF优化，就是双向队列优化，在spfa压入队列时，判断要压入队首还是队尾。这个优化可以优化15%~20%。

  • spfa的LLL优化，就是记录现在队列中元素所代表值的平均值，和要压入元素的值相比较，如果大于平均值，直接压入对列尾部，LLL优化+SLF优化可以优化大概50%。

10.4.3 Floyd算法

• Floyd算法（弗洛伊德）：解决全源最短路问题，即给定图G(V,E)，求任意两点u，v之间的最短路径长度。时间复杂度O(V³)。由于复杂度决定顶点数不超过200个，所以使用点为关键的邻接矩阵来实现Flloyd算法比较合适。

• 基本思想：

  • dis[i][j]表示顶点i和顶点j的最短距离

  • 遍历顶点k∈[1,n]，枚举所有顶点对（i∈[1,n],j∈[1,n]），如果存在顶点k，使得k作为中介点，顶点i到j的当前最短距离缩短，则使用顶点k作为两者的中介点。即dis[i][k] + dis[k][j] < dis[i][j]时，令dis[i][j] = dis[i][k] + dis[k][j] - 遍历三次顶点所以时间复杂度O(V³)

// 伪代码
枚举顶点k∈[1,n]
	以顶点k作为中介点，枚举所有顶点对(i,j)
		如果dis[i][k] + dis[k][j] < dis[i][j]成立
			赋值dis[i][j] = dis[i][k] + dis[k][j]
			
// 邻接矩阵版Floyd算法
#include<cstdio>
#include<allgorithm>
using namespace std;
const int INF = 10000000;
const int MAXV = 200;
int n, m;
int dis[MAXV][MAXV];

void Floyd(){
	for(int k = 0; k < n; k++){
		for(int i = 0; i < n; i++)
			for(int j = 0; j < n; j++)
				if(dis[i][k] != INF && dis[i][k] + dis[k][j] < dis[i][j] && dis[k][j] != INF)
					dis[i][j] = dis[i][k] + dis[k][j];
}

int main(){
	int u, v, w;
	fill(dis[0], dis[0] + MAXV * MAXV, INF);
	scanf("%d%d",&n, &m);
	for(int i = 0; i < n; i++)
		dis[i][i] = 0;
	for(int i = 0; i < m; i++)
	{
		scanf("%d%d%d",&u, &v, &w);
		dis[u][v] = w;
	}
	Floyd();
	for(int i = 0; i < n; i++){}
		for(int j = 0; j < n; j++)
			printf("%d",dis[i][j]);
		printf("\n")
	}
	return 0;
}

10.5 最小生成树

10.5.1 最小生成树及其性质

• 最小生成树（Minimum Spanning Tree,MST）：无向图中求一棵树，满足整棵树的边权之和最小，且连接所有图中所有顶点。

  • 最小生成树是树，其边数=顶点数-1，且树内一定不会有环

  • 对给定图G，其最小生成树可以不唯一，但是其边权之和一定唯一

  • 由于最小生成树在无向图上生成，因此其根结点可以是这棵树上任意一个节点。如果题目中涉及最小生成树的输出，为了让最小生成树唯一，一般都会直接给出根结点（初始节点），只需要通过根结点求解最小生成树即可。

• prim / kruskal算法，都是采用贪心策略，只不过策略不一样。

10.5.2 prim算法

• prim（普里姆）算法：图(V,E)，设置集合S存放访问点。

  • 每次从集合V-S中选择与集合S最短距离最小的顶点u，访问并加入集合S。（用set存储，也可以用bool型数组vis[]存储）

  • 令u为中介点，优化所有能从u直接相连的顶点v与集合S之间的最短距离。上述操作循环n次直至所有点加入进来。

// 伪代码 
//G为图，数组d为顶点与集合S的最短距离
Prim(G,d[]){
	初始化;
	for(循环n次){
		u = 使d[u]最小还未被访问的顶点标号;
		记u已被访问;
		for(从u出发能到达的所有顶点v){
			if(v未被访问&&以u为中介点使得v与集合S的最短距离d[v]更优)
				将G[u][v]赋值给v与集合S的最短距离d[v]；
		}
	}
}

const int MAXV = 1000;
const int INF = 100000000;

// 邻接矩阵版prim算法
int n, G[MAXV][MAXV];
int d[MAXV];
bool vis[MAXV] = {false}
int prim(){
	fill(d, d + MAXV, INF);
	d[0] = 0;
	int ans = 0;
	for(int i = 0; i < n; i++){
		int u = -1, MIN = INF;
		for(int j = 0; j < n; j++)
			if(vis[j] == false && d[j] < MIN){	// 找到未被访问并且最短距离最小的点u
				u = j;
				MIN = d[j];
			}
		// 找不到小于INF的d[u],则剩下的顶点和集合S不连通
		if(u == -1) return -1;
		vis[u] = true;
		ans += d[u];
		for(int v = 0; v < n; v++)
			// v未访问&& u能到达v &&以u为中介点可以使v离集合S更近
				if(vis[v] == false && G[u][v] != INF && G[u][v] < d[v])
					d[v] =G[u][v]
	}
	return ans; //返回边权之和
}

// 邻接表版prim
struct Node{
	int v, dis;
};
vector<Node> Adj[MAXV];
int n;
int d[MAXV];
bool vis[MAXV] = {false};

int prim(){
	fill(d, d + MAXV, INF);
	d[0] = 0;
	int ans = 0;
	for(int i = 0; i < n; i++){
		int u = -1, MIN = INF;
		for(int j = 0; j < n; j++){
			if(vis[j] == false && d[j] < MIN){
				u = j;
				MIN = d[j];
			}
		}
		if(u == -1) return -1;
		vis[u] = true;
		ans += d[u];
		for(int j = 0; j < Adj[u].size();j++){
			int v = Adj[u][j].v;
			if(vis[v] == false &&Adj[u][j].dis < d[v])
				d[v] = G[u][v];
		}
	}
	return ans;
}

• 时间复杂度O(V²)，在选出最短距离最小步骤可以跟Dijkstra算法一样通过小根堆优化使时间复杂度将为O(VlogV+E)。
  • 由复杂度说米国尽量在顶点数目少(V少)而边数较多的情况下使用prim算法

10.5.3 kruskal算法

• kruskal（克鲁斯卡尔）算法：prim采用的是对点贪心的策略从而收纳所有点，而kruskal算法采用的是对边贪心的策略。

  • 初始状态图中每个顶点都自成一个连通块（相当于集合），对所有边按边权从小到大进行排序

  • 按边权从小到大测试所有边（该题直接将E(图的边)sort排序），如果当前测试边所连接的两个顶点不在同一个连通块(集合)中则把这条边加入最小生成树集合中，否则舍弃。

  • 直至最小生成树中的边数等于总顶点数-1或者测试完所有边时结束。如果结束时最小生成树边数小于总顶点数，则说明此图不连通。

  • 根据上述可知，对于kruskal算法可以使用并查集高效实现。

// 伪代码
int kruskal(){
	令最小生成树的边权之和为ans,最小生成树的当前边数Num_Edge;
	将所有边按边权从小到大排序;
	for(从小到大枚举所有边){
		if(当前测试边的两个端点在不同的连通块中){
			将改测试边加入最小生成树中;
			ans += 测试边的边权;
			最小生成树的当前边数Num_Edge加1;
			当边数Num_Edge等于顶点数-1时结束循环;
		}
	}
	return ans;
}

// 并查集实现kruskal算法
int father[N];
int find Father(int x){
	...
}

int kruskal(int n, int m){
	int ans = 0, Num_Edge = 0;
	for(int i = 1; i <= n; i++)
		father[i] = i;
    sort(E,E+m,cmp)
    for(int i = 0; i <m; i++){
    	int faU = findFather(E[i].u);
    	int faV = findFather(E[i].v);
    	if(faU != faV){
    		father[faU] = faV;
    		ans += E[i].cost;
    		Num_Edge++;
    		if(Num_Edge == n-1) break;
    	}
    }
    if(Num_Edge != n-1) return -1;
    else return ans;
}

• kruskal算法时间复杂度O(ElogE)，所以kruskal算法适用于顶点数多，边数较少的情况，与prim算法相反。所以一般对于最小生成树算法的选择，如果是稠密图（边数多）则用prim算法，如果是稀疏图（边数少）则用kruskal算法。

// 完整题解
#include<cstdio>
#include<algorithm>
using namespace std;
const in MAXV =110;
const int MAXE = 10010;

// 边集定义
struct edge{
	int u,v;
	int cost;
}E[MAXE];
bool cmp(edge a, edge b){
	return a.cost < b.cost;
}

int father[N];
int find Father(int x){
	...
}

int kruskal(int n, int m){
	int ans = 0, Num_Edge = 0;
	for(int i = 1; i <= n; i++)
		father[i] = i;
    sort(E,E+m,cmp)
    for(int i = 0; i <m; i++){
    	int faU = findFather(E[i].u);
    	int faV = findFather(E[i].v);
    	if(faU != faV){
    		father[faU] = faV;
    		ans += E[i].cost;
    		Num_Edge++;
    		if(Num_Edge == n-1) break;
    	}
    }
    if(Num_Edge != n-1) return -1;
    else return ans;
}

int main(){
	int n, m;
	scanf("%d%d", &n, &m);
	for(int i = 0; i < m; i++)
		scanf("%d%d%d", &E[i].u, &E[i].v, &E[i].cost);
	int ans = kruskal(n,m);
	printf("%d",ans);
	return 0;
}

10.6 拓扑排序

10.6.1 有向无环图

• 如果一个有向图任意顶点都无法通过一条路径回到自身，那么则称该图为有向无环图（Directed Acyclic Graph,DAG）

10.6.2 拓扑排序

• 拓扑排序是将有向无环图G的所有顶点排成一个线性序列，使得对图G中如果存在边u->v则在序列中u一定在v前面。这个序列被称为拓扑序列。

  • 如果两个顶点之间没有直接或者间接的先导关系，则两点在序列中的顺序是任意的（eg. 课程学习，如果没有前置关系，则先学后学哪个都可以）

  • 拓扑排序的重要应用就是怕判断一个图中是否是有向无环图。

• 思路：

  • 首先定义一个队列，将所有入度为0的结点入队（如果有输出要求，则可以改为某规则的优先队列）

  • 取队首元素，输出。然后删除所有从该结点出发的边（相当于该结点的所有邻接结点入度-1），再判断若某个顶点入度减为0，则入队。循环直至队列为空。

  • 如果队列为空跳出时，入队结点的数目恰好为N，则说明拓扑排序成功。否则拓扑排序失败，图G中有环。

10.7 关键路径

10.7.1 AOV网和AOE网

• 顶点活动（Activity On Vertex，AOV）网是指用顶点表示活动，而用边集表示活动间优先关系的有向图。（eg. 拓扑排序中的先导课程，顶点表示课程(活动)，边表示课程的先导关系(活动间的优先关系)） - 同样AOV网中不存在有向环，否则会让优先关系出现逻辑错误

• 边活动（Activity On Edge，AOE）网是基于工程提出的概念，指用带权的边集表示活动，而用顶点表示事件的有向图，边权表示完成活动需要的时间。（eg. 项目活动图） - 同样AOE网不存在环，否则会出现逻辑问题。

  • AOE网一般只有一个源点和一个汇点（入度为0和出度为0的点，想象工程只有一个起始时刻和结束时刻）。

  • 但是实际上可以有多个源点和汇点，那么就要添加一个“超级源点 / 汇点”，连接指向所有的入度为0 / 出度为0的点，边权为0，这样就可以变成通常的AOE网

• AOV网转AOE网：AOV网表活动前后置关系，AOE网就详细表明了活动进程。

  • 将AOV网每个顶点(活动)拆成两个顶点，分别表示该活动的起点和终点；用有向边连接，边权表示活动时间。原AOV网的边边权设为0，表示上个活动的终点到这个活动的起点不需要花时间。最后再添加“超级源点 / 汇点”

  • eg. AOV：⚪1—⚪2，AOE：⚪1(起)—5—⚪1(终)—0—⚪2(起)—4—⚪2(终)

• AOE网中的最长路径被称为关键路径，而路径上的活动被称为关键活动。关键活动影响整个工程的进程，关键路径的长度为整个工程的最短完成时间。（后续还有松弛时间等概念，该节未在涉及）

10.7.2 最长路径

• 求解最长路径：对一个没有正环的图（即指从源点可达的正环），如果需要求最长路径，实际上可以将所有边设置为边权乘以-1，令其变为相反数，这样再使用Bellman-Ford算法或SPFA算法求最短路径即可。（Dijkstra不能处理负边权）

  • 如果求的是有向无环图的最长路径长度，则10.7.3中关键路径的求法比上述算法更快

• 如果图中有正环，最长路径显然不存在，但是如要求最长简单路径（每个顶点最后只经过一次的路径），即便存在也没办法通过Bellman-Ford等算法来求解，因为最长路径问题是NP-Hard问题（没有多项式时间复杂度算法的问题）

10.7.3 关键路径

• 求关键路径就是：求解有向无环图（DAG）中最长路径的方法

• 方法：

  • 求解关键路径，等同于找到一条路径，路径上的活动都是关键活动。

  • 关键活动的最早开始时间 = 最迟开始时间，因此可以设置数组e[r]和l[r]，分别表示活动r的最早开始时间和最晚开始时间，通过e[r] == l[r]判断活动r是否为关键活动 - 边的属性求解

  • 顶点Vi经过活动r后到达顶点Vj。设置数组ve和vl，其中ve[i]和vl[i]分别表示事件i的最早发生时间和最迟发生时间（eg. 项目中该项目的最早开始时间和最晚开始时间），将求解e[]和l[]转为求ve[]和vl[] - 点的属性求解

    • ⚪(Vi)—r—⚪(Vj)

    • 对活动r来说，只要事件Vi最早发生时马上开始，那麽e[r] = ve[i]，中间没有一点拖延。

    • 如果l[r]是活动r最迟发生时间，那么l[r] + length[r]就是vj的最迟发生时间（length[r]表示边权），所以l[r] = vl[j] - length[r]。

  • 接下来就是求解ve[]和vl[]

    • 对于每一个ve[i]最早开始时间而言，是往前看前驱结点，根据前驱结点决定值，假设k,j是i的前驱，eg. k—>i<—j

    • 则有ve[i] = max{ve[j,k] + length[rj,rk]}，那么如果想要获得ve[i]的值，就需要获得所有前驱的值 - 通过拓扑排序来进行这个过程

    • 对于上述的ve[i]的更新过程，是当我们遍历i的每个前驱结点时对它进行更新，而不是遍历到i时再去找前驱结点。所以更新过程就是：遍历结点，更新该结点的后继结点的ve[]值

    • 对于每一个vl[i]最晚开始时间而言，是往后看后继结点，根据后继结点决定值，假设k,j是i的后继， eg. k<—i—>j

    • 则有ve[i] = min{ve[j,k] - length[rj,rk]}，那么如果想要获得ve[i]的值，就需要获得所有后继的值 - 通过逆拓扑排序来进行这个过程，而逆拓扑序列只需把拓扑序列翻转即可得到（入栈出栈）

  • 综上所述就是：

    • 先求点：通过拓扑序和逆拓扑序计算各顶点的ve[] = max{ve[]+length[]} & vl[] = min{vl[] - length}

    • 再求夹边：e = ve[i] & l[] = vl[] - length[]，然后判断每个结点的e[] == l[]既可

// 拓扑序列
stack<int> topPrder;
// 拓扑排序，顺便求ve[]
bool topologicalSort(){
	queue<int> q;
	for(int i = 0; i < n; i++){	// 找到入度为0
		if(inDegree(i) == 0)
			q.push(i);
	}
	while(!q.empty()){
		int u = q.front();	// 每个front结点就是当前遍历的结点
		q.pop();
		topPrder.push(u);
		for(int i = 0; i < G[u].size(); i++){	
			int v = G[u][i].v;
			inDegree[v]--;
			if(inDegree[v] == 0)
				q.push(v);
			// 用u来更新所有后继结点v
			if(ve[u] + G[u][i].w > ve[v])
				ve[v] = ve[u] + G[u][i].w;
		}
	}
	if(topPrder.size() == n) return ture;
	else return false;
}

// 更新vl,初始值为终点的ve值 - 因为终点的vl=ve
fill(vl, vl + n, ve[n-1]);
//topPrder出栈即为逆拓扑序列，求解vl数组
while(!topOrder.empty()){
	int u = topOrder.top();
	topOrder.pop();
	for(int i = 0; i < G[u].size(); i++){
		int v= G[u][i].v;
		if(vl[v] - G[u][i].w < vl[u])
			vl[u] = vl[v] = G[u][i].w;
	}
}

//关键路径主体部分代码，不是有向无环图则返回-1，否则返回关键路径长度
int CriticalPath(){
	memset(ve,0,sizeof(ve));
	if(topologicaSort() == false){	// 拓扑排序
		return -1;
	}
	fill(vl, vl + n, ve[n-1]);
    while(!topOrder.empty()){
        int u = topOrder.top();
        topOrder.pop();
        for(int i = 0; i < G[u].size(); i++){
            int v= G[u][i].v;
            if(vl[v] - G[u][i].w < vl[u])
                vl[u] = vl[v] = G[u][i].w;
        }
    }
    
    // 遍历邻接表的所有边，计算e&l (e&l没有存储起来，如果需要存储，可以定义在结点Node中作为属性)
    for(int u = 0; u < n; u++){
    	int v = G[u][i].v, w = G[u][i].w;
    	int e = ve[u], l = vl[v] - w;
    	// 如果e==l，则说明u->v是关键路径
    	if(e == l)	printf("%d->%d\n",u,v);
    }
    return ve[n-1]	//返回关键路径长度
	
}

• 如果事先不知道汇点编号，则是根据ve[]数组的最大值来表示。ve[]最大值一定是汇点，所以只需要fill函数前添加一段语句，改变下vl函数初始值即可

int maxLenght = 0;
for(int i = 0; i < n; i++){
	if(ve[i] > maxLenght) maxLength = ve[i];
}
fill(vl,vl+n,maxLength);

• 还可以使用动态规划来更加简洁求解关键路径的代码

第十一章 提高篇(5) - 动态规划专题

11.1 动态规划的递归写法和递推写法

11.1.1 什么是动态规划

• 动态规划（Dynamic Programming DP）：一种用爱解决一类最优化问题的算法思想。
  • 简单来说就是将一个复杂问题分解成若干个子问题，并且这些子问题会重复出现，称这个问题拥有重叠子问题 Overlapping Subproblems；一个问题的最优解可以通过其子问题的最优解有效构造出来，那么称这个问题拥有最优子结构 Optimal Substructure，只有问题同时具备两者性质才能够使用动规来解决。

11.1.2 动态规划的递归写法

• 传统的暴力递归是不会存储每次计算的值，比如每次遇到F(1)他都要执行一次，那么将其优化下就是使用一个cache数组来存储每次递归的值，下次遇到相同的递归就可以直接调用值而不需要浪费资源。 - 是一种从递归到动规的中间版本，叫记忆化搜索

• 斐波那契数列的记忆化搜索实现

int F(int n ){
	if(n == 0 || n == 1) return 1;
	if(dp[n] != -1) return dp[n];
	else{
		dp[n] = F(n-1) + F(n-2);
		return dp[n];
	}
}

11.1.3 动态规划的递推写法

• 动规：

  • 从暴力递归中延申 - 过程中还经历过<记忆化搜索>，相当于暴力递归+cache缓存(用hashmap实现)，他并没有状态方程依赖，只是单纯的记忆并给出。

  • 把暴力递归的过程，抽象成状态转移 - 子函数的嵌套调用转换成数组序号的关系(依赖)

  • 并且存在可能化简状态转移使其更简洁的过程（状态方程的化简）

    • eg. 格子值等于上一行该格子位置上前数Σ；状态方程(A+B+C) = A+B+C；化为动规就是将上一行该格子位置上前数组索引Σ - 再化简就是该格子值等于上格子值+左格子值；状态方程(A+B+C) = ((A+B)+C)，(A+B)是左格子，C是上格子

  • 动态规划用数组记录子问题解，优化过程与状态转移方程有关，与原始题目相关性不大

    • 暴力递归的可变参数 = 动规数组几维表 - 解空间大小

    • 确定目标点；确定basecase（不依赖项）；return 返回结果

    • 如何设计状态和状态转移方程是动态规划的核心与难点

11.2 最大连续子序列和

• 题目：给定要给数字序列A1,A2...An，求i,j使得Ai+...Aj最大，输出这个最大和。eg. -2,11,-4,13,-5,-2，则显然11+(-4)+13最大。

• 思路：

  • 暴力枚举左右端点再计算A[i]+..A[j]，时间复杂度O(n³)；记录前缀和，时间复杂度O(n²)，优化了A[i] + ..A[j] = S[j] - S[i-1]过程降了一个维度。

  • 动规：暴力递归的可变参数只有一个，就是遍历i - dp[i]表示以A[i]为结尾的连续序列最大和。最后返回的就是dp[]数组中的最大值，时间复杂度O(n)，只需要遍历一遍数组即可。

    • 边界条件：dp[0] = A[0]

    • 状态转移方程：dp[i] = max{A[i],dp[i-1]+A[i]} - 就是选和不选两种状态

    • 状态的无后效性：当前状态记录了历史状态，一旦确定就不会改变，且未来的决策只能在当前已有状态基础上进行。eg. 每次计算状态dp[i]只会设计dp[i-1]，而不直接用到dp[i-1]蕴含的历史信息。

#include<cstdio>
#include<algorithm>
using namespace std;
const int maxn = 10010;
int A[maxn],dp[maxn];	//A[]存放序列
int main(){
	int n;
	scanf("%d",&n);
	for(int i = 0; i < n; i++) scanf("%d",&A[i]);
	dp[0] = A[0];
	for(int i = 1; i < n; i++){
		dp[i] = max(A[i], dp[i-1]+A[i]);
	}
	int k = 0;
	for(int i = 1; i < n; i++){
		if(dp[i] > dp[k])
			k = i;
	}
	printf("%d\n",dp[k]);
	return 0;
}

11.3 最长不下降子序列（LIS）

• 题目：在一个数字序列中，找到一个最长的子序列（可以不连续），使得这个子序列是不下降（非递减）得。

  • 最长不下降序列 Longest Increasing Sequence LIS

• 思路：

  • 暴力枚举：选或者不选这个数两个选项，判断目前序列是否是不下降序列，边界条件就是枚举结束，得到最大长度maxLength，时间复杂度O(2ⁿ)。

  • 跟最长连续子序列之和一样，可变参数是遍历i - dp[i]表示以A[i]为结尾的最长不下降子序列。最后返回的dp[]数组的最大值。

  • 边界条件：dp[0] = 1

  • 状态转移方程：dp[i] = max{1, dp[j]+1} - j是i前面并且A[i] >= A[j] & dp[j]+1 > dp[i]的下标（所以需要遍历，时间复杂度O(n²)）

#include<cstdio>
#include<algorithm>
using namespace std;
const int N = 100;
int A[N], dp[N];
int main(){
	int n;
	scanf("%d",&n);
	for(int i = 1; i <= n; i++)	scanf("%d",&A[i]);
	int ans = -1;
    for(int i = 1; i <= n; i++){
        dp[i] = 1;
        for(int j = 1; j < i; j++)
            if(A[i] >= A[j] && (dp[j] + 1 > d[i]))
                dp[i] = dp[j] + 1;
		ans = max(ans, dp[i]);
    }
	printf("%d",ans);
	return 0;
}

11.4 最长公共子序列（LCS）

• 题目：给定两个字符串（或数字序列）A和B，求一个字符串，使得这个字符串是A和B的最长公共部分（子序列可以不连续）
  • 最长公共子序列 Longeset Common Subsequence LCS
• 思路：

  • 暴力枚举：分别对A/B字符串有选或者不选，两个可变参数i&j - dp[i][j]表示字符串A的i号位和B的j号位之前的两者LCS长度（从1开始），时间复杂度O(n²)

  • eg. A=sadst,B=admin，dp[3][3] 表示sad和adm两者LCS长度

  • 边界条件：dp[i][0] = dp[0][j] = 0

  • 状态转移方程：

    • ① A[i] == B[j]：dp[i][j] = dp[i-1][j-1] + 1

    • ② A[i] != B[j]：dp[i][j] = max

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 100;
int main(){
	int n;
	gets(A+1);	//从下标为1开始读入
	gets(B+1);
	int lenA = strlen(A+1);
	int lenB = strlen(B+1);
	for(int i = 0; i <= lenA; i++){
		dp[i][0] = 0;
	}
	for(int i = 0; i <= lenB; i++){
		dp[0][i] = 0;
	}
	for(int i = 1; i <= lenA; i++){
		for(int j = 1; j <= lenB; j++){
			if(A[i] == B[j])
				dp[i][j] = dp[i-1][j-1] + 1; 
			else dp[i][j] = max(dp[i-1][j], dp[i][j-1]);
		}
	}
	printf("%d\n",dp[lenA][lenB]);
	return 0;
}

11.5 最长回文子串

• 题目：给出一个字符串S，求S的最长回文子串的长度。

• 思想：

  • 暴力解法枚举i和j作为子串两端点，判断S[i..j]是否是回文串（进栈出栈前后是否一样），时间复杂度O(n³)

  • 动规：可变参数两个，左端点跟右端点，dp[i][j]表示S[i] - S[j]字串是否是回文子串，是则为1，不是为0。时间复杂度O(n²)

  • 边界条件：dp[i][i] = 1，dp[i][i+1] = 1/0（S[i] ?= S[s+1]）

  • 状态转移方程：

    • ① S[i] == S[j]：dp[i][j] = dp[i+1][j-1]

    • ② S[i] !=S[j]：dp[i][j] = 0

  • 与之前动规不同的是，这里的j需要进行两次循环，分别处理奇回文和偶回文（右端点直接根据子串length）

#include<cstdio>
#include<cstring>
const int maxn = 1010;
char S[maxn];
int dp[maxn][maxn];
int main(){
	gets(S);
	int len = strlen(S), ans = 1;
	memset(dp,0,sizeof(dp));
	// 边界
	for(int i = 0; i < len; i++){
		dp[i][i] = 1;
		if(i < len +1){
			if(S[i] == S[i+1]){
				dp[i][i+1] = 1;
				ans = 2;
			}
		}
	}
	for(int L = 3; L <= len; L++){
		for(int i = 0; i + L -1 < len; i++){
			int j = i + L -1;
			if(S[i] == S[j] && dp[i+1][j-1] == 1){
				dp[i][j] 1;
				ans = L;
			}
		}
	}
	printf("%d\n",,ans);
	return 0;
}

• 其他解法：二分+字符串hash，时间复杂度O(nlogn)；Manacher马拉车法添加辅助标志，时间复杂度O(n)；新增字母判断是否仍然是回文（python使用切片比马拉车快），时间复杂度O(n)

11.6 DAG最长路

• 题目：求解有向无环图中的最长路径（或者最短路径）

  • ①：求整个DAG中的最长路径（不固定起点跟终点）

  • ②：固定终点，求DAG的最长路径

• ① 思路：

  • dp[i]表示从i号顶点出发能获得最长路径长度，这样所有dp[i]的最大值就是DAG最长路径长度

  • 从最后的汇点往前溯源求解dp[]数组 - 对于i顶点的dp[i] = max{dp[j] + length[i->j]} 找出最大的后继顶点距离+边距离

    • 因为需要所有后继结点，所以可以用逆拓扑序列（每个后继顶点对其进行更新），但是也可以不通过你拓扑序列，直接使用递归计算。

  • 所有顶点初始化dp[]=0，出度不为0的点会递归求解。int型choice[]数组记录最长路径上顶点的后继顶点，也可以改成vector类型数组（多条最长路径） - 求解最长路径条数（参考Dijkstra算法条数计算）

  • dp[i]也可以去表示以i号顶点结尾能获得最长路径长度，状态转移矩阵是找到最大的前驱顶点距离+边距离。但是相比上述表示而言，无法去选出多条同样最长路径的最小字典序路径，上述的自动实现了最小字典序。

// 只计算最长距离
int DP(int i){
	if(dp[i] > 0) return dp[i];
	for(int j = 0; j < n; j++)
		if(G[i][j] != INF)
			dp[i] = max(dp[i], DP[j] + G[i][j]);
}

// 计算长度并求解路径结点
int DP(int i){
	if(dp[i] > 0) return dp[i];
	for(int j = 0; j < n; j++){
		if(G[i][j] != INF){
			int temp = DP(j) + G[i][j];
			if(temp > dp[i]){
				dp[i] = temp;
				choice[i] = j;
			}
		}
	}
	return dp[i];
}

// 调用printPath前需要先得到最大的dp[i]，然后将i作为路径起点传入
void printPath(int i){
	printf("%d",i);
	while(choice[i] != -1){
		i = choice[i];
		printf("->%d",i);
	}
}

• ②思路：

  • 与①差不多，dp[i]仍然表示从i号顶点出发到达终点T能获得的最长路径长度，状态转移方程仍然是：dp[i] = max{dp[j] + length[i->j]} ，从后继顶点溯源。

  • 不同的是边界条件，①中的边界条件是dp[汇点]=0，所有dp[]初始化为0；②中的边界条件是dp[T]=0，这里不能将所有初始化为0，因为会有一些节点无法到达终点T（例如汇点），合适的做法是初始化dp[]为-INF来保证无法到达终点的含义，然后设置一个vis数组表示定点是否已经被计算

int DP(int i){
	if(vis[i]) return dp[i];
	vis[i] = true;
	for(int j = 0; j < n; j++){
		if(G[i][j] != INF)	//负最大值
			dp[i] = max(dp[i], DP[j] + G[i][j]);
	}
	return dp[i];
}

• 许多的问题都可以视为DAG最长路问题：比如经典的矩形嵌套问题

  • 矩形嵌套问题：给出n个矩形长和宽，定义矩形的嵌套关系为矩形A长宽都相比大于矩形B长宽，。先求一个矩阵序列，长度最长；如果有多个，则选择矩阵编号序列的字典序最小的那个。

  • 将每个矩阵堪称顶点，并将嵌套关系看作有向边，边权均为1。

11.7 背包问题

• 背包问题是一类经典的动规问题，本节只介绍最简单的两种：01背包和完全背包问题。

11.7.2 01背包问题

• 题目：有n件物品，每件物品的重量为w[i]，价值为c[i]。现有一个容量为V的背包，问如何选取物品放入背包，使得背包内物品的总价值最大。其中每件物品都只有一件。

• 思路：

  • 暴力递归每件物品拿或不拿，时间复杂度O(2ⁿ)

  • 动规dp[i][v]表示前i件物品目前背包容量为v所获得的最大。时间复杂度O(nV)

  • 状态转移方程：

    • ①：如果拿第i件物品，dp[i][v] = dp[i-1][v-w[i]] + c[i]

    • ②：如果不拿第i件物品，dp[i][v] = dp[i-1][v]

    • 因为要获得最大价值所以为：dp[i][v] = max{dp[i-1][v-w[i]] + c[i]， dp[i-1][v]}·

  • 边界条件：dp[0][v] = 0

for(int i = 1; i <= n; i++)
	for(int v = w[i]; v <= V; v++)
		dp[i][v] = max(dp[i-1][v-w[i]] + c[i]， dp[i-1][v])

• 对空间复杂度的优化：

  • 计算dp[i][v]时只需要dp[i-1][v]左侧的数据（即dp[i-1][0..v]，并且不会用到dp[i][0..v]的数据），且当计算dp[i+1][]时又不需要dp[i-1][]了要用dp[i][] - 所以可以只开一个一维数组dp[v]，枚举方向改变为i从1到n，v从V到0（逆序)，空间复杂度O(V)

  • 状态转移方程：dp[v] = max(dp[v]，dp[v-w[i]] + c[i])

  • 这样节约压缩数组空间的技巧称为滚动数组

// 压缩后动规
for(int i = 1; i <= n; i++){
	for(int v = V; v >= w[i]; v--)
		dp[v] = max(dp[v], dp[v-w[i]]+c[i]);
}

// 完整求解01背包代码
#include<cstdio>
#include<algorithm>
using namespace std;
const int maxn = 100;
const int maxv = 1000;
int w[maxn], c[maxn], d[maxv];
int main(){
	int n,V;
	scanf("%d%d",&n,&V);
	for(int i = 0; i < n; i++)	scanf("%d",&w[i]);
	for(int i = 0; i < n; i++)	scanf("%d",&c[i]);
	for(int i = 0; i < n; i++)	dp[i] = 0;
	for(int i = 1; i <= n; i++){
	for(int v = V; v >= w[i]; v--)
		dp[v] = max(dp[v], dp[v-w[i]]+c[i]);
	}
	int max = 0;
	for(int v = 0; v <= V; v++)
		if(dp[v] > max)	max = dp[v];
	printf("%d\n",max);
	return 0;
}

11.7.3 完全背包问题

• 题目：有n种物品，每种物品的单件重量为w[i]，价值为c[i]。现有一个容量为V的背包，问如何选取物品放入背包，使得背包内物品的总价值最大。其中每件物品都有无穷件。

  • 完全背包与01背包的区别就是物品件数。

• 思路：

  • 同样dp[i][v]表示第i件物品目前背包容量为v。

  • 对于物品一样还是拿或者不拿，但是状态转移方程有所不同，因为如果拿了第i件物品，还可以继续拿第i件物品，只有到了选择不拿的时候，才会与前后物品发生关系。（因为是已知第一个所以是从前往后求，会与前面物品发生关系）

  • 状态转移方程：dp[i][v] = max{dp[i][v-w[i]] + c[i]， dp[i-1][v]}，因为拿了之后还可以继续拿，所以转到的是dp[i][v-w[i]]状态。

  • 同样可以对空间进行优化，改成一维形式：dp[v] = max(dp[v], dp[v-w[i]] + c[i])，对v的枚举正向枚举，与01背包一维相反。

  • 边界条件：dp[0][v] = 0 & dp[v] = 0

for(int i = 1; i <= n; i++)
	for(int v = w[i]; v <= V; v++)
		dp[v] = max(dp[v], dp[v-w[w] + c[i]]);

11.8 动态规划规律总结

• 之前介绍的动规模型dp[]含义

  • 最大连续子序列和：dp[i]表示以A[i]作为末尾的连续序列的最大和

  • 最长不下降子序列LIS：dp[i]表示以A[i]作为末尾的最长不下降子序列长度

  • 最长公共子序列LCS：dp[i][j]表示字符串A的i号位和B的j号位之前的LCS长度

  • 最长回文子串：dp[i][j]表示S[i]至S[j]子串是否是回文串

  • 灯塔dp[i][j]表示从第i行第j个数字出发到达最底层所有路径上所得到的最大和

  • DAG最长路：dp[i]表示从i号顶点出发能获得的最长路径长度

  • 01背包问题：dp[i][v]表示第i件物品当前容量为v的背包获得最大价值

  • 完全背包：dp[i][v]表示第i件物品当前容量为v的背包获得最大价值

• 规律总结：

  • 当题目与序列或者字符串（记为A）有关时：

    • dp[i]表示以A[i]结尾（或开头）的 XXX

    • dp[i][j]表示A[i]至A[j]区间的 XXX

  • 分析题目种的状态需要几维来表示时（可变参数几个），对其中每一维采取以下某表述

    • 恰好为i

    • 前i

    • 然后dp[][]数组含义为恰好为i，前j...的 XXX ，通过端点特征构造转移方程

    • 大多数情况下都可以把动规问题看作一个DAG，图中结点时状态，边就是状态转移方向，求解顺序就是按照DAG拓扑序进行求解。

第十二章 提高篇(6) - 字符串专题

12.1 字符串hash进阶

• 字符串hash是指将一个字符串S映射为一个整数，使得该整数可以尽可能唯一地代表字符串S。

  • 之前讲过对只有大写字符串的字符串hash，他将字符串当作二十六进制的数，然后将其转换为十进制。其中str[i]表示字符串i号位，index函数将A-Z转为0-25，H[i]表示字符串前i个字符的hash值。

  • H[i] = H[i-1] * 26 + index(str[i])

  • 虽然这样可以使一一对应，但是因为进制较大，当字符串较长时产生整数会非常大，为了处理这样的情况只能舍弃一些唯一性，对hash结果取模mod。

  • H[i] = (H[i-1] * 26 + index(str[i])) % mod

  • 但是这样会造成可能多个字符串hash值相同，不过实践中发现把进制数设置为一个10⁷级别的素数p（eg. 10000019），同时把mod设置为一个10⁹级别的素数（eg. 100000007），这样冲突会变得非常小。

  • H[i] = (H[i-1] * p + index(str[i])) % mod

• 问题：给出N个只有小写字母的字符串，求其中不同的字符串的个数

  • 可以使用上述的字符串hash函数（p+mod），也可以直接用set或者map，但会慢一点点

#include<iostream>
#include<string>
#include<vector>
#include<algoriithm>
using namespace std;
const int MOD = 100000007;
const int P = 10000019;
vector<int> ans;

// 字符串hash
long long hashFunc(string str){
	long long H = 0;
	for(int i = 0; i < str.length(); i++)
		H = (H * P + str[i] - 'a') % MOD;
	return H;
}

int main(){
	string str;
	while(getline(cin,str), str != "#"){
		long long id = hashFunc(str);
		ans.push_back(id);
	}
	sort(ans.begin(), ans.end());
	int count = 0;
	for(int i = 0; i < ans.size(); i++)
		if(i == 0 || ans[i] != ans[i-1])
			count++;
	cout<< count << endl;
	return 0;
}

• 求解字符串子串的hash值，也就是求解H[i...j]：

  • H[i..j]实际上也就等于str[i..j]从p进制转换成十进制的结果

  • H[i..j] = index(str[i] * p^j-i) + index(str[i+1] * p^j-i-1) +... + index(str[j] * p⁰)

  • H[j] = H[j-1] * p + index(str[j])
    = (H[j-2] * p + index(str[j-1])) * p + index(str[j])
    = H[i-1] * p^j-i+1 + H[i..j]

  • 所以将H[i..j] 转化，并加上取模操作，为了使结果非负，最后再加上mod再次取模得到hash结果

  • H[i..j] = ((H[j] - H[i-1] * p^j-i+1) % mod + mod) % mod

• 问题：输入两个长度均不超过1000的字符串，求他们的最长公共子串的长度（子串必须连续）。

  • 该题应该可以用动规做出来

  • 分别对两个字符串每个子串求出hash值，找到两堆子串对应hash相等并最大的子串，时间复杂度O(n² + m²)

#include<iostream>
#include<cstdio>
#include<string>
#include<vector>
#include<algoriithm>
#include<map>
using namespace std;
typedef long long LL;
const LL MOD = 100000007;
const LL P = 10000019;
const LL MAXN = 1010;
// powP[i]存放P^i%MOD,H1和H2分别存放str1和str2的hash值
LL powP[MAXN], H1[MAXN] = {0}, H2[MAXN] = {0};
// PR1存放str1的所有<子串hash值，子串长度>，pr2同理
vector<pair<int,int>> pr1,pr2;

// 初始化powP函数
void init(int len){
	powP[0] = 1;
	for(int i = 1; i <= len; i++)
		powP[i] = (powP[i-1] * p) % MOD;
}

// calH函数计算字符串str的hash值
void calH(LL H[], string & str){
	H[0] = str[0];
	for(int i = 1; i < str.length(); i++)
		H[i] = (H[i-1] * P + str[i]) % MOD;
}

// calSingleSubH计算H[i..j]
int calSingleSubH(LL H[], int i, int j){
	if(i == 0) return H[j];
	return  ((H[j] - H[i-1] * powP[j-i+1]) % MOD + MOD) % MOD
}

// calSubH计算所有子串的hash值，并将键值对存入pr中
void calSubH(LL H[], int len, vector<pari<int,int>> &pr){
	for(int i = 0; i < len; i++)
		for(int j = i; j < len; j++){
			int hashvalue = calSingleSubH(H, i, j);
			pr.push_back(make_pair(hashvalue, j-i+1))
		}
}

// 计算pr1和pr2中相同的hash值，维护最大长度
int getMax(){
	int ans = 0;
	for(int i = 0; i < pr1.size(); i++)
		for(int j = 0; j < pr2.size(); j++)
			if(pr1[i].first == pr2[j].first)
				ans = max(ans, pr1[i].second);
	return ans;
}

int main(){
	string str1,str2;
	getline(cin,str1);
	getline(cin,str2);
	init(max(str1.length(),str2.length()));
	calH(H1,str1);
	calH(H2,str2);
	calSubH(H1,str1.length(),pr1);
	calSubH(H2,str2.length().pr2);
	printf("ans = %d\n",getMax());
	return 0;
}

• 问题：最长回文子串，用hash+二分思路解决，时间复杂度O(nlogn)

  • 对给定字符串str，先求出其字符串hash数组H1，然后再将str反转求出其反转字符串hash数组H2，再根据回文串奇偶情况讨论

  • ① 回文串长度是奇数：枚举回文中心点i，二分子串的半径k，找到最大的k使子串[i - k, i + k]是回文串。判断回文串等价于判断str的两个子串[i - k, i]与[i , i + k ]是否是相反的串，等价于判断str[i-k , i]与反转串rstr[len-1-(i+k), len-1-i]是否相同。

  • ② 回文串长度是偶数：枚举回文空隙点，令i为空隙左边第一个元素下标，则找到最大的k使得[i-k+1, i+k]是回文串。与之前相同，判断字符串str的[i-k+1, i]子串是否与rstr的[len-1-(i+k), len-1-(i+1)]子串是否相同。

// 代码过长见书<算法笔记> 12.1节

• 如果极其针对使用此组p+mod的hash字符串，可以调整p+mod对，也可以使用效果更强的双ahsh法，即指用两个hash函数生成的整数组合表示一个字符串。

• 本节介绍的hash函数只是众多zifuchuanhash方法中的一种，即从进制转换角度进行字符串hash，除此之外还有一些很好的hash函数如BKDRhash，ELFhash，都有非常好的效果。

12.2 KMP算法

• 本节讨论字符串匹配问题：如果给出两个字符串text和pattern，需要判断pattern是否是text的子串。

  • text称为文本串，pattern称为模式串。

• 暴力做法：枚举text每个字符，与pattern进行遍历匹配，时间复杂度O(nm)。

• KMP算法：时间复杂度O(n+m)，因为是由Knuth, Morris, Pratt三个科学家发现的，所以算法名称叫KMP算法。

12.2.1 next数组

• 假设一个字符串s（下标从0开始），以i号位作为结尾的子串就是s[0..i]，对该子串而言，长度为k+1的前缀与后缀分别是s[0..k]和s[i-k..i]。

• 现定义一个int型数组next，next[i]表示使子串s[0..i]的前缀s[0..k]等于后缀s[i-k..i]的最大k值（前后缀可部分重叠，但不能是其本身），如果找不到相等的k值则next[i] = -1 - next[i]等于所求最长相等前后缀中前缀最后一位的下标。

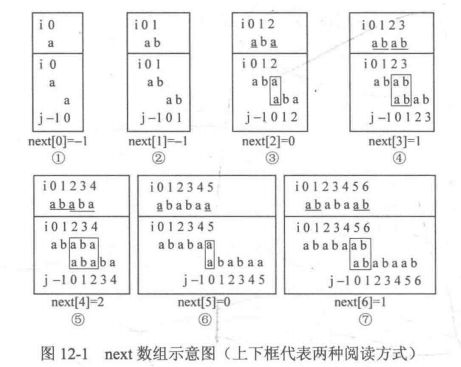
• 过程见上图，以字符串s = "ababaab"为例

  1. i = 0：子串s[0..i]为"a"，由于找不到相等前后缀（因为前后缀不能为本身），所以next[0] = -1

  2. i = 1：子串 s[0..i]为"ab"，由于找不到相等前后缀，所以next[1] = -1

  3. i = 2：子串 s[0..i]为"aba"，能找到当k=1时的前后缀相同，所以next[2] = 0（最长相等前后缀中前缀最后一位的下标）

  4. i = 3：子串 s[0..i]为"abab"，能找到当k=2时的前后缀相同，所以next[3] = 1（最长相等前后缀中前缀最后一位的下标）

• 一般使用递推的方式求解next[]数组，即假设已知next[0]~next[i-1]，求解next[i]

  • 以上图为例了，现来求解next[4]，s="ababa"，next[3]=1，j=next[3]

    • 首先判断最长前后缀，因为next[3]=1，所以我们长度将其加1看看是否相等，即s[4-(j+1)...4] ?= s[0...j+1] - "aba"=="aba"，成立，所以next[4]=next[3]+1=2，之后将j指向next[4]

  • 继续我们求解next[5]，s="ababaa"，next[4]=2

    • 跟上一样，s[5-(j+1)...5] ?= s[0...j+1] - "abab != abaa"，不成立，我们就要缩小k的取值，找到一个合适的值令其成立。

    • 我们希望k尽可能的大，但又符合。我们只需令j = next[j]，然后不断判断s[i-(j+1)...i] ?= s[0...j+1]，循环直至最后，next[i] = j+1；在i=5时，当j = next[next[next[4]]]=-1时，s[i..i] == s[0..0]，所以next[5] = 0

  • 所以总的求解该过程如下：

    • 初始化next数组，令j=next[0]=-1

    • 让i遍历，对每个i执行以下两步，求解next[]

    • 判断s[i-j-1...i] ?= s[0...j+1]，等于则next[i]=j+1，j=next[i]；否则令`next[i]=j,j=next[i]，继续判断直到回退为-1。

// getNext求解长度为len的字符串s的next数组
void getNext(char s[], int len){
	ing j = -1;
	next[0] =-1;
	for(int i = 1; i <len; i++){
		while(j != -1 && s[i] != s[j+1])	j = next[j];
		if(s[i] == s[j+1]){
			j++;
		}
		next[i] = j;
	}
}

12.2.2 KMP算法

• 问题：文本串text和模式串pattern，判断模式串pattern是否是文本串text的子串。

• 令i指向text的当前欲比较位，令j指向pattern的当前已被匹配的最后一位。这样只要text[i] == pattern[j+1]成立就说明匹配成功。此时让i++,j++继续比较，直到j到了m-1成功结束

• 当text[i] != pattern[j+1]，则要找另一个j'使得text[i] == pattern[j'+1]，这就联想到了next数组。next数组的含义就是当j+1匹配失败的的时候j应该回退到的位置。text串就是s[i]，pattern串就是s[j+1]。

• KMP算法一般思路：

  • 初始化j=-1，表示pattern当前已被匹配的最后位。

  • 让i遍历文本串text，对每个i，执行下两步试图匹配text[i]和pattern[j+1]

  • 不断令j = next[j]，直到j回退为-1，或是text[i] == pattern[j+1]成立

  • 如果text[i] == pattern[j+1]，令j++，如果j达到m-1，说明pattern是text子串，返回true。

// kmp算法
bool KMP(char text[], char patternp[]){
	int n = strlen(text), m = strlen(pattern);
	getNext(pattern, m);
	int j = -1;
	for(int i = 0; i < n; i++){
		while(j != -1 && text[i] != pattern[j+1])	j = next[j];
		if(text[i] == pattern[j+1])	j++;
		if(j == m-1) return true;
		return false;
	}
}

• 问题：如何统计文本串text中模式串pattern出现的次数。

• 只需要在之前的基础上稍作修改，当进行一次成功匹配后，即j=m-1后，i++，我们不能让j从最前面开始，而是让其回退一定距离即可，从上可联想到是next[j]。

// KMP算法，统计pattern在text中出现的次数
int KMP(char text[], char pattern[]){
	int n = strlen(text), m =strlen(pattern);
	getNext(pattern, m);	// O(m)
	int ans = 0, j = -1;
	for(int i = 0; i < n; i++){		// O(n)
		while(j != -1 && text[i] != pattern[j+1])	// 平摊到每次for循环就是O(1)级别
			j = next[j];
		if(text[i] == pattern[j+1])	j++;
		if(j == m-1){
			ans++;
			j = next[j];
		}
	}
	return ans;
}

• 对KMP算法的优化：

  • 在匹配失败后j回退，中间有些步骤是可以优化的，因为回退无意义需要继续回退，试想能否修改next[j]存放的内容，让它可以可以跳过无意义的回退部分，一步回退到正确的位置让成立。

  • 这个优化只需要在求解next数组基础上稍作修改即可得到，让一直回退判断pattern[i+1] != pattern[j+1]。优化后的next数组叫做nextval数组，不再是最长相等前后缀含义，改为了当模式串pattern的i+1位发生时配时，i应当回退到的最佳位置。（pattern[i+1] != pattern[j+1]时表示只需要回退一次就到最优位置了）

void getNextval(char s[], int len){
	int j = -1;
	nextval[0] = -1;
	for(int i = 0; i < len; i++){
		while(j != -1 && s[i] != s[j+1])	j = nextval[j];
		if(s[i] == s[j+1])	j++;
		// 此处和getNext不同
		if(j == -1 || s[i+1] != s[j+1])	nextval[i] = j;
		else nextval[i] = nextval[j];
	}
}

// 对于后续KMP都一样，可以把while替换成if，因为最多也就执行一次。

12.2.3 从有限状态自动机角度看待KMP算法

• 有限状态机，终态就是pattern模式串的最后匹配，输入的text文本串就是正规式。

• 把自动状态机推广为树形，就是字典树（前缀树）。可以解决多维字符串匹配问题，即一个文本串（输入）匹配多个模式串（树的分支路径）的匹配问题。通常把这种算法称为AC自动机，KMP算法只是AC自动机的特殊形式。

第十三章 专题拓展

13.1 分块思想

• 查询过程中元素可能发生改变（例如插入、修改或删除），称为在线查询。查询过程中元素不发生改变，就称为离线查询。

• 问题：给出一个非负整数序列A，元素个数为N，在有可能随时添加或删除元素的情况下，实时查询序列元素第k大，即把序列元素从小到大排序后从左到右的第k个元素。

• 实时序列第k大元素有很多种解法，本节要将的是其中较容易理解，写法简介的做法：分块思想

  • 分块就是把有序元素划分为若干块

  • 首先对一个有N个元素的有序序列来说，除最后一块外，其余每块中元素个数都应该为[sqrt(N)]向下取整，于是块数为[sqrt(N)]向上取整。

  • 暴力的做法添加和删除元素时需要O(n)复杂度来移动元素，而对于分块，先设置一个hash数组table[100001]，其中table[x]表示整数x的当前存在个数；接着借助分块思想从逻辑上将0~10⁵分为317块，其中每块元素个数316块。

  • 再定义一个统计数组block[317]，其中block[i]表示第i块中存在的元素个数

  • 思想类似于OS/计组的相联，分块分区，如果想要添加 / 删除元素，直接用[x/316]算出块号，让block[]++，table[x]++，时间复杂度O(1)。

  • 以上解决了实时数据更新，接下来解决查询序列中第k大的元素。

  • 首先从小到大枚举块号，判断找出第k大的元素所在分块。然后从小到大遍历该块中每一个元素（其中i号块的第一个元素是table[i*316]），利用table数组继续累加元素的存在个数，直到总累计数达到k找到第k大元素。

  • 时间复杂度为O(sqrt(N)+sqrt(N))=O(sqrt(N))

• 题目：给出一个栈的入栈（Push），出栈（Pop）过程，并随时通过PeekMedian命令要求输出栈中中间大小的数（Pop命令输出出栈的数）。当栈中没有元素时，Pop和PeekMedian输出Invalid。

  • 本题除了设计栈的插入和弹出操作的同时，还要实时支持查询栈内元素第k大。

  • 栈内元素在hash角度来看跟普通序列元素没有什么区别，所以可以用分块思想来解决该问题，只需要在Push命令时添加元素，Pop命令时删除元素。对于N次查询，总时间复杂度为O(N * sqrt(N))

  • 牛客网算法中也讲过一个类似的题，实时数据流输出中位数，使用的是大小根堆来实现的。添加数据时间复杂度O(logn)，取中位数时间复杂度O(1)。

13.2 树状数组（BIT）

13.2.1 lowbit运算

• lowbit运算：lowbit(x) = x & (-x) - 二进制的每位与运算，(-x)相当于x包括符号位取反+1，两者再相与，得到的必然是（x二进制最右边的1，其他位都是0），也能理解为能整除x的最大2的幂次（eg.lowbit(6) = 2²）

13.2.2 树状数组及其应用

• 问题：给出一个整数序列A，元素个数为N，接下来查询k次，每次查询将给出一个正整数x，求A的前x个整数之和。

  • 对于该问题，一般的做法是开一个sum数组，其中sum[i]表示前i个整数之和（数组下标从1开始），这样sum数组就可以在输入序列A的时候进行预处理，每次查询直接输出sum[x]即可。

  • 升级问题：假设在查询过程中随时可能给第i个整数加上一个整数v进行序列更新，要求在查询中能实时输出最新序列前x个整数之和。更新和查询总次数为k次

  • 对此还是之前的做法，sum[]数组预处理，只不过更新的时候需要把sum[i]以及后面所有sum[]都加上整数v而已。这样会使得更新操作时间复杂度O(N)，若是更新占多则总时间复杂度会变化O(KN)。

  • 若是不使用sum数组，直接对原数组进行更新查询的话，则虽然更新O(1)，但是查询变成了O(N)。

  • 至此引入了树状数组的概念，可以很好的解决这个问题。

• 树状数组（Binary Indexed Tree BIT）：仍然是一个数组，类似于sum[]，是一个用来记录和得数组，只不过他存放得不是前i个整数之和，而是在i号位之前（含i号位，下同）lowbit(i)个整数之和。

  • 假设A[]是原始数组，有A[1]~A[16]共十六个元素；数组C是树状数组，其中C[i]存放**数组A中i号位之前（包括）lowbit(i)个元素之和 **，形象可见下图。显然C[i]覆盖长度是lowbit(i)，是按2的幂次递增的

    • eg. C[1]管辖范围lowbit(1)=1，管A[1]，C[2]管辖范围lowbit(2)=2，管A[1,2]，C[3]管辖范围lowbit(3)=1，管A[3]，C[4]管辖范围lowbit(4)=4，管A[1,2,3,4] .......

    • 树状数组的定义非常重要，重点是C[i]覆盖长度是lowbit(i)，另外数组下标必须从1起

• 接下来，如何利用树状数组解决之前两个问题：

  • ①设计getSum(x)返回前x个数之和：A[1]+...A[x]

  • ②设计update(x,v)实现将第x个数加上一个数v的功能：A[x]+=v

• getSum(x)设计：

  • 从树状数组定义出发可知，C[x] = A[x-lowbit(x)+1] + .... + A[x]

  • sum[x] = A[0] + ... + A[x] = A[0] + ... + A[x-lowbit(x)] + C[x] = sum[x-lowbit(x)] + C[x]

  • 根据以上式子可以继续将 sum[x-lowbit(x)] 进行递归 / 递推拆分

  • 从二进制角度来看，由于lowbit(x)的作用是定位x二进制的最右边的1，所以可以把x-=x-lowbit(x)看作是不断把x最右边的1置为0直至没有的过程。所以for循环执行次数就是x二进制中1的个数，最多是logN次。所以时间复杂度是O(logN)

  • 从另一个角度上来看，根据之前的图，getSum(x)相当于一个树往左上追溯的过程，因为树高最多O(logN)，所以时间复杂度也是O(logN)

  • 另外如果要求数组下标在区间[x,y]内的数之和，那么相当于getSum(y) - getSum(x-1)来解决，这是一个很重要的技巧。

int getSum(int x){
	int sum = 0;
	for(int i = x; i > 0; i -= lowbit(i))	//是i>0而非i>=0
		sum += c[i];
	return sum;
}

• upDate(x,v)设计：

  • 假如让A[6]加上一个数v，那么就要找到所有C[]覆盖A[6]的元素。

  • 首先从C[6]一定是最接近的C[]元素，再从C[6]往上追溯，依次近的一个一个找。实际上就是找到一个尽可能小的整数a，使得lowbit(x+a) > lowbit(x)。很容易知道最小的a就是lowbit(x)，这样会产生进位，导致最右边1一定比lowbit(x)最右边1大。

  • 所以update函数的做法就是，不断让x加上lowbit(x)，每个C[x]都加上v，直至x超过A[]数组边界。

  • 从二进制角度来看这个过程就是从右至左不断定位x二进制最右边1左边0的过程，所以时间复杂度O(logN)，同样从树状理解，update就是结点沿右上追溯的过程，直至越界。

void undate(int x,int v){
	for(int i = x; i <= N; i += lowbit(i)	c[i] += v;
}

• 经典应用：给定一个有N个正整数的序列A，对序列中的每个数，求出序列中它左边比它小的数的而个数

  • hash数组解法：遍历每个数，将其加入hash数组中，然后遍历hash数组比他小的索引对应的值累加即可，即hash[0]+hash[1]...+hash[i]

  • 树状数组：getSum(i - 1)和update(i,1)可以解决这个问题，前者累加后者相当于hash更新

  • 如果要统计序列左边比该元素大的个数，就等价于计算getSum(N)-getSum[A[i]]。至于统计元素右边比左边小（大）的元素个数，只需要把原始数组从右往左遍历即可。

#include<cstdio>
#include<cstring>
const int maxn =10010;
#define lowbit(i) ((i)&(-i))
int c[maxn];

void update(int x, int v){...}
int getSum(int x){...}

int main(){
	int n, x;
	scanf("%d",&n);
	memset(c, 0, sizeof(c));
	for(int i = 0; i < n; i++){
		scanf("%d", &x);
		update(x,1);
		printf("%\n", getSum(x-1));
	}
	return 0;
}

• 如果A[i]开的很大，比如A[]序列为{520, 999999999,18,666}，这样的话我们只需要考虑他们之间的大小关系，实际上与序列{2,5,1,3,4}是等价的。因此就是要做的是把A[]数组与1~N进行映射

  • 可以设置一个临时的结构体数组，用来存放元素值和原始序号，再输入完成后将数组按val从小到大进行排序，排序完后把原始序号pos存入一个新的数组中，这样就做成了一个完美映射。

  • 这样的技巧称之为离散化

  • 一般来说，离散化只适用于离线查询，因为必须要确定所有出现的元素后才能进行离散化；对在线查询也能做一定手段，可先把所有操作的记录下来再按照操作顺序正常进行“在线”查询即可。

#include<cstdio>
#include<cstring>
#include<algoritm>
using namespace std;
const int maxn = 10010;
#define lowbit(i) ((i)&(-i))
struct Node{
	int val;
	int pos;
}temp[maxn];
int A[maxn];
int c[maxn];

void update(int x, int v){...}
int getSum(int x){...}

bool cmp(Node a, Node b){
	return a.val < b.val;
}

int main(){
	int n;
	scanf("%d",&n);
	memset(c,0,sizeof(c));
	for(int i = 0; i < n; i++){
		scanf("%d".&temp[i].val);
		temp[i].pos = i;
	}
	sort(temp, temp + n, cmp);
	for(int i = 0; i < n; i++){
		if(i == 0 || temp[i].val != temp[i-1].val) A[temp[i].pos] = i+1;
		else A[temp[i].pos] = A[temp[i-1].pos];
	}
	for(int i = 0; i < n; i++){
		update(A[i],1);
		printf("%d\n",getSum[A[i]-1]);
	}
	return 0;
}

• 用树状数组求解序列第k大问题：

  • 若是用hash数组记录每个元素出现个数，那么序列第k大就是在求最小的i使得hash[1]+..hash[i] >= k成立，等价于寻找第一个满足条件getSum(i) >= k的i。

  • 由于hash数组的前缀和是递增的，可以根据二分来找到合适的mid判断getSum(mid)>=k。总时间复杂度O(logN) * O(logN)

int findKthElement(int K){
	int l = 1, r = MAXN, mid;
	while(l < r){
		mid = (l+r)/2;
		if(getSum(mid) >= K) r= mid;
		else l = mid + 1;
	}
	return l;
}

• 问题：如果给定的是一个二维整数矩阵A，求解A[1][1]~A[x][y]这个子矩阵中所有元素之和，并且怎么给单点添加整数v。
  • 实际上把树状数组推广为二维即可，具体做法就是直接把update和getSum函数中的for循环改为两种即可。如果求A[a][b]~A[x][y]之和，则只需计算getSum(x,y)-getSum(x-1,y)-getSum(x,y-1)+getSum(x-1,y-1)即可，更高维的情况就是把for循环改成相应维度即可。

int c[maxn][maxn];
void update(int x, int y, int v){
	for(int i = x; i < maxn; i += lowbit(i)){
		for(int j = y; j <= maxn; j += lowbit(j))	c[i][j] += v;
	}
}
int getSum(int x, int y){
	int sum = 0;
	for(int i = x; i > 0; i -= lowbit(i)){
		for(int j = y; j > 0; j -= lowbit(j))	sum += c[i][j];
	}
	return sum;
}

• 前面的都是对树状数组的单点更新、区间查询，如果想要进行区间更新、单点查询？

  • ① 设计函数getSum(x)，返回A[x]

  • ② 设计函数update(x,v)，讲A[1]~A[x]的每个数都加上一个数v

  • 按照原先定义的话update不可能达到时间复杂度O(logN)，所以需要对树状数组的定义进行修改。 - C[i]还是跟之前一样的覆盖长度lowbit(i)，只不过不再表示这段区间的元素之和，而是表示这段区间每个数当前被加了多少。

    • eg. C[16] = 0表示A[1]_{A[16]都被加了0，C[8]=5表示A[1]}A[8]都被加了5

  • 很容易发现，A[x]值实际上就是覆盖它的若干个"矩形"C[i]的值之和，相当于之前的update作为了现在的getSum，

  • 同理可以把之前的getSum函数作为现在的update函数

int getSum(int x){
	int sum  = 0;
	for(int i = x; i < maxn; i += lowbit(i)){
		sum += c[i];
	}
	return sum;
}

void update(int x, int v){
	for(int i = x; i > 0; i -= lowbit(i))
		c[i] += v;
}