学习笔记：三角恒等变换（正在更新）

诱导公式

• 公式 第一组

  \[\sin(\alpha+2k\pi)=\sin\alpha \]
  \[\cos(\alpha+2k\pi)=\cos\alpha \]
  \[\tan(\alpha+2k\pi)=\tan\alpha \]

  推导： 同终边的三角函数值相等

  应用： 把任意角度的三角函数值转化为 \(0\) ~ \(2\pi\) 角的三角函数值

• 公式 第二组

  \[\sin(\alpha+\pi)=-\sin\alpha \]
  \[\cos(\alpha+\pi)=-\cos\alpha \]
  \[\tan(\alpha+\pi)=\tan\alpha \]

  推导：

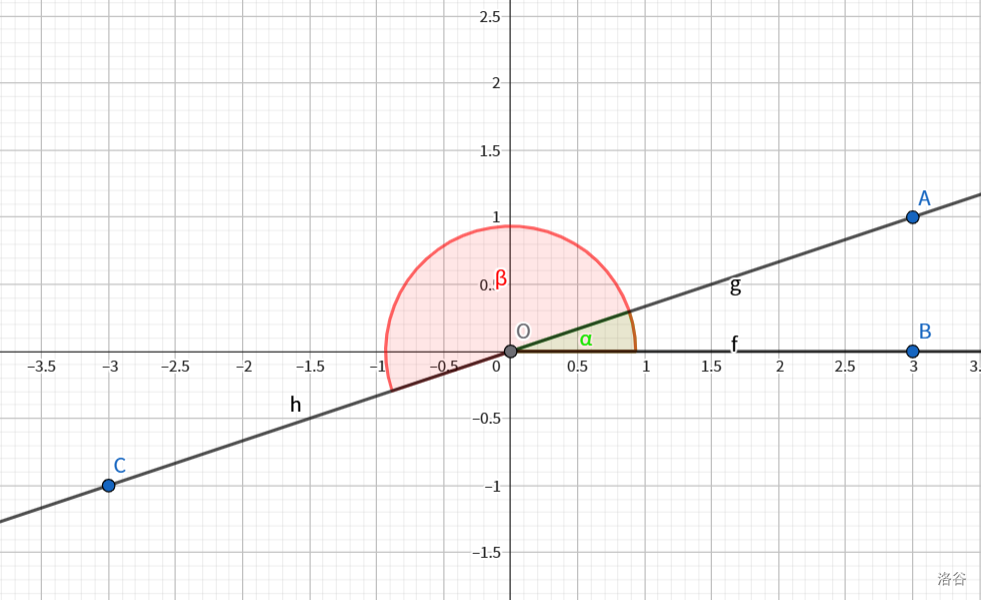
  设 \(\alpha\) 为锐角，将其放入平面直角坐标系，根据三角函数定义，即单位圆上 \(P(\cos\alpha,\sin\alpha)\)。将其逆时针旋转 \(\pi\) 度，得到新角，如图：

  
  观察到新角的 \(\sin\) 值和原角互为相反数， \(\cos\) 同理。最后由 \(\tan\alpha=\frac{\sin\alpha}{\cos\alpha}\) 即可得出。

  应用： 把 \(0\) ~ \(2\pi\) 的三角函数值转化为 \(0\) ~ \(\pi\) 的三角函数值

• 公式 第三组

  \[\sin(\pi-\alpha)=\sin\alpha \]
  \[\cos(\pi-\alpha)=-\cos\alpha \]
  \[\tan(\pi-\alpha)=-\tan\alpha \]

  推导：

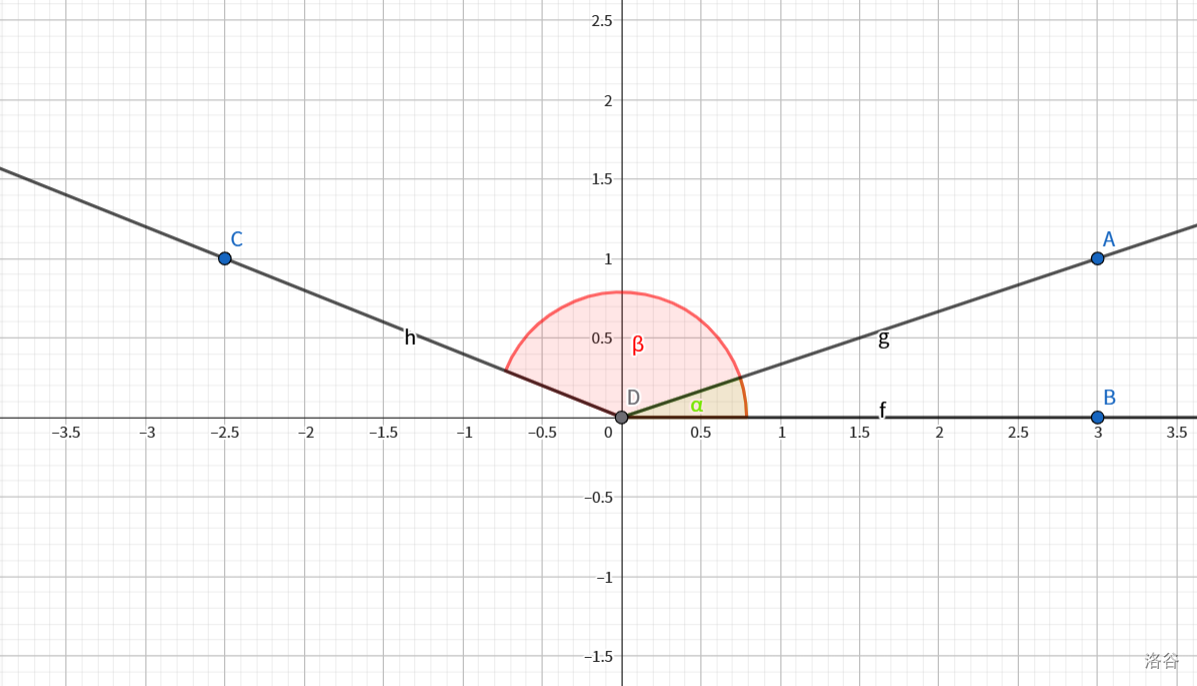
  原理同上，将角放入平面直角坐标系即可得出。如图：

  

  应用： 把 \(0\) ~ \(2\pi\) 的三角函数值转化为 \(0\) ~ \(\pi\) 的三角函数值

• 公式 第四组

  \[\sin-\alpha=-\sin\alpha \]
  \[\cos-\alpha=\cos\alpha \]
  \[\tan-\alpha=-\tan\alpha \]

  推导：

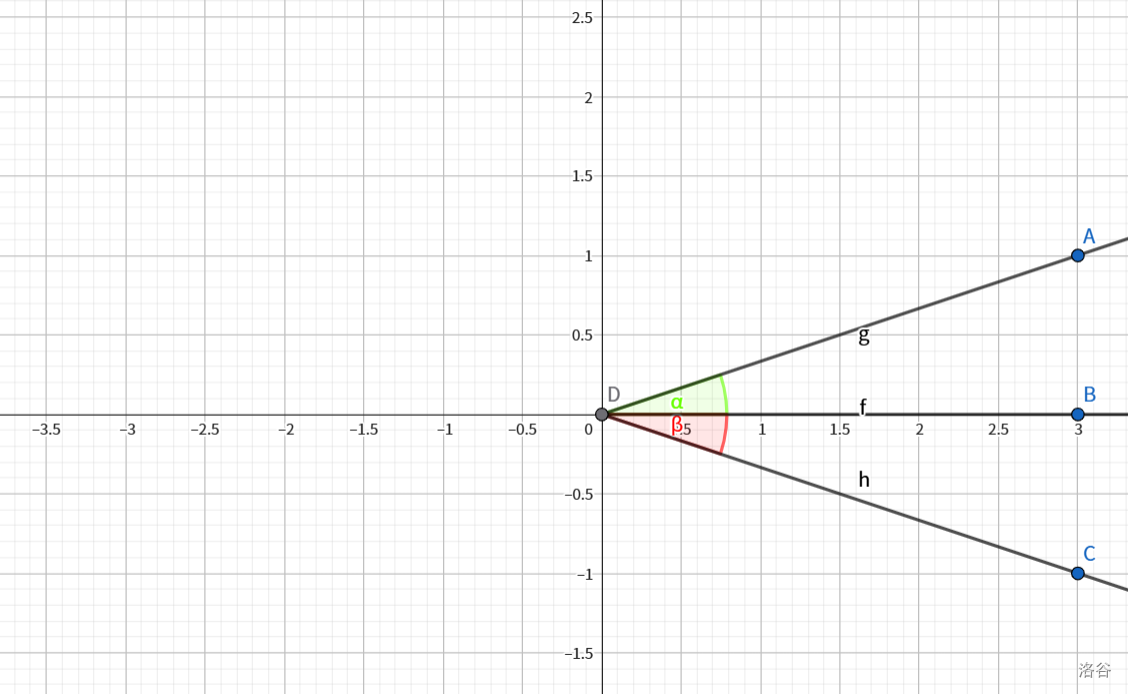
  原理同上，将角放入平面直角坐标系即可得出，如图：

  

  应用： 把 \(0\) ~ \(2\pi\) 的三角函数值转化为 \(0\) ~ \(\pi\) 的三角函数值

• 公式 第五组

  \[\sin(\alpha+\frac{\pi}{2})=\cos\alpha \]
  \[\cos(\alpha+\frac{\pi}{2})=-\sin\alpha \]

  推导：

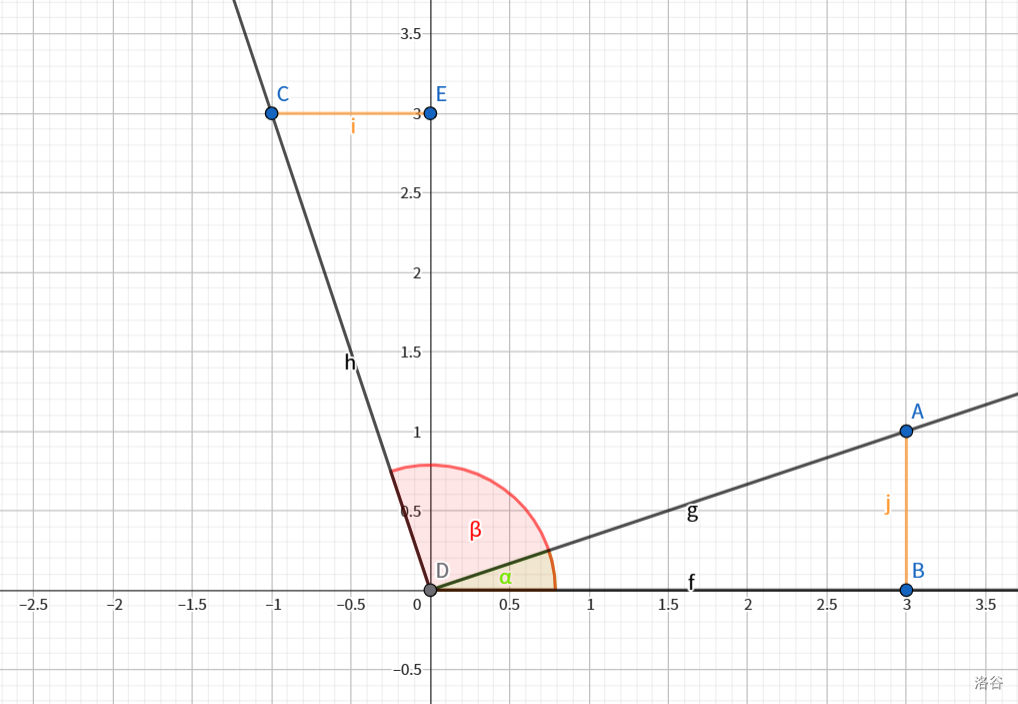
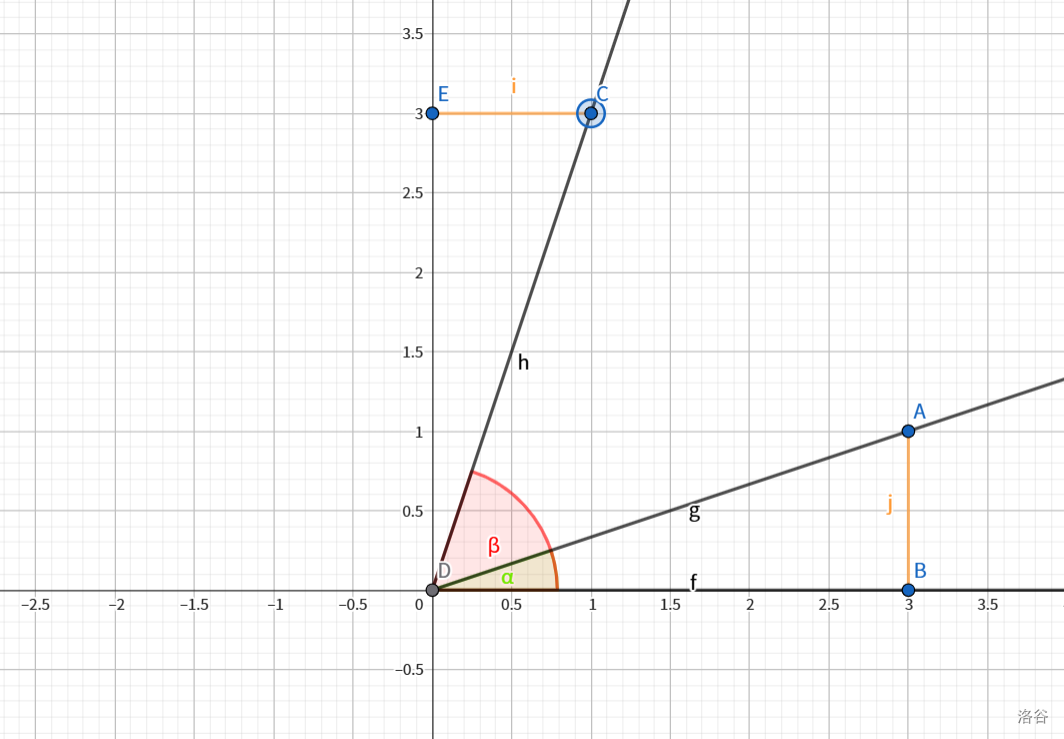
  将角放入平面直角坐标系，如图：

  

  这里讲一下证明。

  不难证明此时\(\triangle DCE\cong\triangle DAB\)。为了方便我们设 \(AD=CD=1\)，则 \(AB=\sin\alpha，CE=\cos\beta=\cos(\frac{\pi}{2}+\alpha)\)，由于此时 \(\cos\beta\) 在第二象限，值为负，所以前面添上一个负号，即 \(\cos(\alpha+\frac{\pi}{2})=-\sin\alpha\)。
  \(\sin\) 的推导同理，不再讲述。

  应用： 把 \(0\) ~ \(\pi\) 的三角函数值转化为 \(0\) ~ \(\frac{\pi}{2}\) 的三角函数值

• 公式 第六组

  \[\sin(\frac{\pi}{2}-\alpha)=\cos\alpha \]
  \[\cos(\frac{\pi}{2}-\alpha)=\sin\alpha \]

  推导： 原理同上，将角放入平面直角坐标系即可得出。如图：

  

  应用： 把 \(0\) ~ \(\pi\) 的三角函数值转化为 \(0\) ~ \(\frac{\pi}{2}\) 的三角函数值

至此，所有诱导公式介绍完毕。不需要死记硬背，有一句口诀：奇变偶不变，符号看象限。 就是说当加了 \(\frac{\pi}{2}\) 的奇数倍时， \(\sin\) 和 \(\cos\) 的函数名互换，偶数倍则保持原函数名。确定函数名后只需要通过锐角，画图或想象旋转相应角度之后的情况即可。

三角恒等变换

学完了前置，现在终于可以开始正题了。

• 和角公式、差角公式

  和角公式

  \[\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta \]
  \[\cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta \]

  推导：
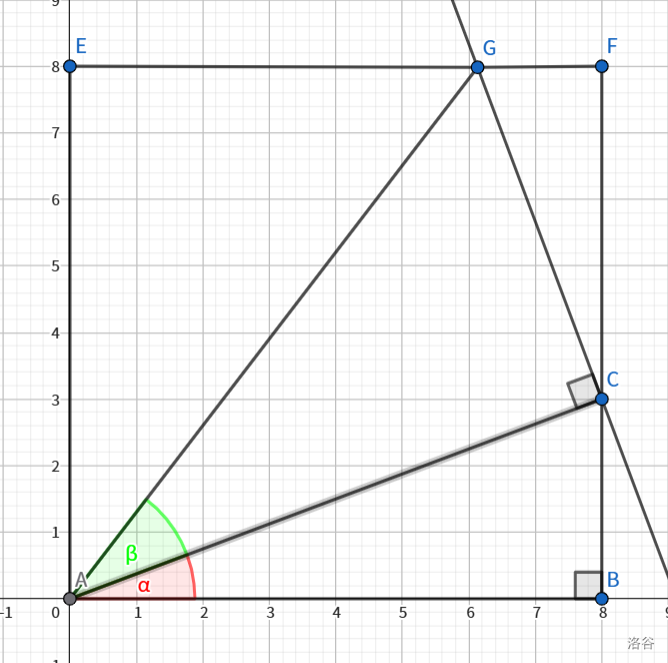
  先画图形如图：

  

  \(EABF\) 为长方形。为了推导方便，我们设 \(AG=1\)。

  \(\therefore CG=\sin\beta, AC=\cos\beta\)

  \(\therefore AB=\cos\beta\cos\alpha,BC=\cos\beta\sin\alpha\)

  \(\because \angle ACB+\angle GCF=90\degree,\angle ACB+\angle CAB=90\degree\)

  \(\therefore \angle CAB=\angle GCF\)

  \(\therefore FC=\sin\beta\cos\alpha,GF=\sin\beta\sin\alpha\)

  \(\because \angle EAG=90\degree-\alpha-\beta\)

  \(\therefore AE=\cos(90\degree-\alpha-\beta),EG=\sin(90\degree-\alpha-\beta)\)

  对其应用诱导公式，得

  \(AE=\sin(\alpha+\beta),EG=\cos(\alpha+\beta)\)

  \(\because AE=FC+CB,EG=AB-GF\)

  \(\therefore \sin(\alpha+\beta)=\sin\beta\cos\alpha+\cos\beta\sin\alpha,\cos(\alpha+\beta)=\cos\beta\cos\alpha-\sin\beta\sin\alpha\)

  调整顺序即可得出上述公式。

  将 \(\beta\) 换为 \((-\beta)\)，即可得出

  差角公式

  \[\sin(\alpha-\beta)=\sin\alpha\cos\beta-\cos\alpha\sin\beta \]
  \[\cos(\alpha-\beta)=\cos\alpha\cos\beta+\sin\alpha\sin\beta \]