学习笔记——缩点

前置知识：Tarjan 求强连通分量

一、什么是缩点

缩点，就是把一张有向有环图上的一个个环缩成点，使其变成有向无环图。

二、缩点的应用

• 求最长路时常用。

• 标准问法：

给定一个有向图，每个点有一个权值，允许多次经过一条边或者一个点，重复经过的点，权值只计算一次。求最大权值

若直接用最段路模板改，则会在一个圈子里面一直绕，出不来。所以我们要用缩点，把一个圈缩成一个点，再去求解。

观察下面这张图：

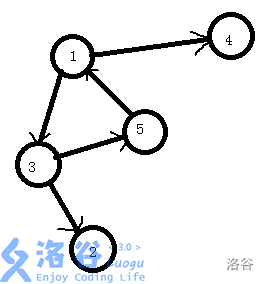
我们会发现，图中点 \(1,3,5\) 形成一个闭环（强连通分量），显然，如果要让这张图的权值最大，我们要把他们都经过一遍。所以缩点，然后把每个点的权值相加。缩完点的图如下：

此点权值为 \(9\)。

三、环的判定

既然我们知道了，有环才能进行缩点，那么怎么判定环呢？先上结论：

当 \(dfn[u]=low[u]\) 时，则点 \(u\) 必然是环上的一点。

为什么？在 Tarjan 求强连通分量的过程中，我们任意一个节点 \(u\) 的 \(low\) 一直在和它的子结点 \(v\) 的 \(low\) 取最小值。那什么情况下， \(low[u]\) 会在取完最小值后仍然和 \(dfn[u]\) （此点的 dfs 序）相等？只能是在 \(u\) 的子树中，有一条返祖边，又指回了 \(u\) 。那么在这种情况下，\(u\) 的子树中部分点和 \(u\) 就成为了一个环。

四、如何进行缩点

在 Tarjan 求强连通分量的基础上，我们在代码中加入一个栈 \(STA\)，用来存放此次 dfs 遍历过的点的编号。另外加入一个标识数组，如果这个点已经在栈中，就不再把它入栈。

当我们判定点 \(u\) 是环中一点时，则栈中且在点 \(u\) 第一次出现之后被压入栈的点一定和点 \(u\) 成为一个环（历经这些点，又环回了 \(u\)）。那么只需要把 \(STA\) 中的这些点作 pop 操作，然后将点权加总，将这些点染上同一个颜色。在所有点 dfs 一遍之后，把颜色不同的点集重新建图连边就可以了（新图每个点集的连边包括原来环上所有点连的所有边）。

核心代码：

//Tarjan算法

void tarjan(int x){
    dfn[x]=low[x]=++num;
    sta[++top]=x, vis[x]=1; //每个点入栈
    //常规求强连通分量
    for (int i=head[x]; i; i=nxt[i]){
        int y=ver[i];
        if(!dfn[y]){
            tarjan(y);
            low[x]=min(low[x], low[y]);
        }
        else if(vis[y]) low[x]=min(low[x], dfn[y]);
    }
    //判定环
    if(low[x]==dfn[x]){
        int y;cnt++;
        //每点弹出栈，到再次遇到点 x 停止
        while(sta[top+1]!=x){
            y=sta[top--];
            col[y]=cnt; //染相同颜色
            vis[y]=0; //标识数组清零
            vsum[cnt]+=p[y]; //权值加和
        }
    }
}

//以下代码添加在main函数中

    tot=0;
    memset(head, 0, sizeof head);
    memset(nxt, 0, sizeof nxt);
    memset(ver, 0, sizeof ver); //清空原图
    for (int i=1; i<=m; i++){  //枚举每一条原边
        int x=col[u[i]], y=col[v[i]]; //每条边的两端点的染色
        if(x!=y) add(x, y); //两端点染色不同，新图里加入连边
    }