机器数运算

一、加法

• 对于无符号数：类似十进制加法

  逢2进1，最高位进位舍去。

• 对于有符号定点数：运用补码运算可以直接带符号位运算

  原码转换为补码的方法：除符号位，也就是数值位按位取反，末位加1。手算时可以从后向前找到第一个1，然后将该1之前的所有数值位取反：
  逢2进1，最高位进位舍去。

  原码与补码的转换：正数的反码、补码与原码一致
  有原码101010
  按位取反变为反码：110101（符号位不变）
  接着末位加1变为补码：110110
  可以发现补码倒数第一个1之前部分1101与反码的前段一致，而后部与原码一致（10）因此可以通过此规律快速从原码转换为补码，反过来补码转换为原码也是一样操作。

二、减法

在计算机中一般将其转化为加法：

• 对于无符号数：

  1.被减数不变，减数全部位按位取反，末位加1。
  2.做加法
  例如：11001110-10101001
  1.将10101001按位取反，变为：01010110；末位加1：01010111
  2.做加法：11001110
  +01010111
  =00100101
  3.验证一下：11001110（206）-10101001（169）=00100101（37）

• 对于有符号定点数：

  通常使用补码运算，同样也是将减法转换为加法：[x]补-[y]补=[x]补+[-y]补
  步骤：
  1.被减数不变，减数全部位按位取反，末位加1。这一步是将[y]补 转为 [-y]补
  2.做加法
  例如：11001110-10101001（补码）
  1.将10101001按位取反，变为：01010110；末位加1：01010111
  2.做加法：11001110
  +01010111
  =00100101
  3.验证一下：11001110（-50）-10101001（-87）=00100101（37）
  总结：可以发现有符号定点数的补码加减法与无符号数操作一致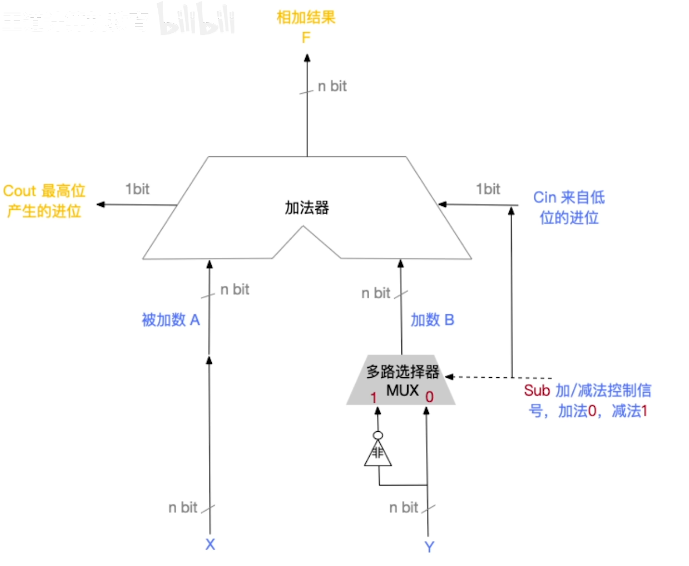

• 溢出的判断 ：

  对于有符号数，有两种判断方式：
  1.用双符号位补码，也就是将0,1101101表示成00,1101101。
  这样在运算是若符号位一致则未发生溢出，若不一致则发生溢出。
  01：表示正溢出，也即是超出最大正数表示范围。
  10：表示负溢出，即超出最小表示范围。
  2.第二种方法是将最高位进位与次高位进位异或运算，也就是OF标志位计算方式：
  异或运算：1⊕0=1；0⊕1=1；1⊕1=0；0⊕0=0；
  结果为1，则表示发生溢出。反之，则没有。

三、乘法

乘法可以分解为加法与移位操作，因此先了解一下移位运算：

1.算术移位：

原反补的算数移位符号位不变仅移动数值位；
(1) 原码的算数移位：左移右移都补零；1,010 右移1位-->1,001
(2) 反码的算数移位：正数时与原码一致；负数时，补1
(3) 补码的算术移位：正数时与原码一致；负数时，右移补1，左移补0。可以用左移补0，右移补符号位来记忆。
2.逻辑移位
整体移位，补0

原码一位乘法