归并排序算法总结（例题：逆序对的数量）

归并排序思维导图：

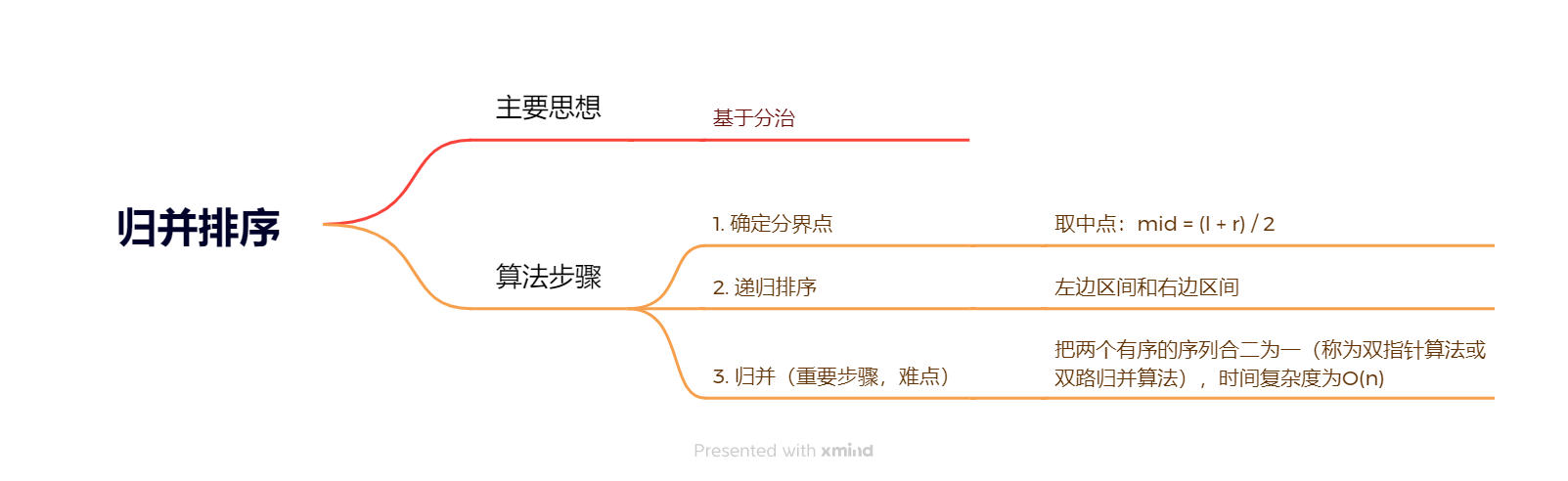
知识点：如果原序列中两个数的值是相同的，它们在排完序后，它们的位置不发生变化，那么这个排序是稳定的。快速排序是不稳定的，归并排序是稳定的。

快排变成稳定的=>使快排排序数组中的每个数都不同，将a_i变成<a_i, i>这个二元组，将a_i的下标也放进来，使用双关键字排序。

快速排序平均时间复杂度是O(nlogn)，最坏是O(n²)，但是基本上不会达到的。归并排序时间复杂度O(nlogn)。

归并排序算法模版：

#include <iostream>

using namespace std;

const int N = 1e5 + 10;

int n;
int q[N], tmp[N];

void merge_sort(int q[], int l, int r)
{
    if (l >= r) return;

    int mid = l + r >> 1;

    merge_sort(q, l, mid), merge_sort(q, mid + 1, r);

    int k = 0, i = l, j = mid + 1;
    while (i <= mid && j <= r)
        if (q[i] <= q[j]) tmp[k++] = q[i++];
        else tmp[k++] = q[j++];
    while (i <= mid) tmp[k++] = q[i++];
    while (j <= r) tmp[k++] = q[j++];

    for (i = l, j = 0; i <= r; i++, j++) q[i] = tmp[j];
}

int main()
{
    scanf("%d", &n);
    for (int i = 0; i < n; i++) scanf("%d", &q[i]);

    merge_sort(q, 0, n - 1);

    for (int i = 0; i < n; i++) printf("%d ", q[i]);

    return 0;
}

 

例题：逆序对的数量

题目链接：

https://www.acwing.com/problem/content/790/

代码：

#include <iostream>

using namespace std;

typedef long long LL;

const int N = 1e5 + 10;

int n;
int q[N], tmp[N];

LL merge_sort(int l, int r)
{
    if (l >= r) return 0;

    int mid = l + r >> 1;
    LL res = merge_sort(l, mid) + merge_sort(mid + 1, r);

    int k = 0, i = l, j = mid + 1;
    while (i <= mid && j <= r)
        if (q[i] <= q[j]) tmp[k++] = q[i++];
        else
        {
            tmp[k++] = q[j++];
            res += mid - i + 1;
        }
    while (i <= mid) tmp[k++] = q[i++];
    while (j <= r) tmp[k++] = q[j++];

    for (int i = l, j = 0; i <= r; i++, j++) q[i] = tmp[j];

    return res;
}

int main()
{
    cin >> n;
    for (int i = 0; i < n; i++) cin >> q[i];

    cout << merge_sort(0, n - 1) << endl;

    return 0;
}