蒙特卡洛法

应用场景：当你无法求得准确值的时候，通过随机取样再进行统计的方式求得近似解。

步骤：

1. 随机抽样

2. 统计实验

3. 求近似解

4. 抽样次数越多，求得近似解接近准确值的概率就越大，即构成统计意义

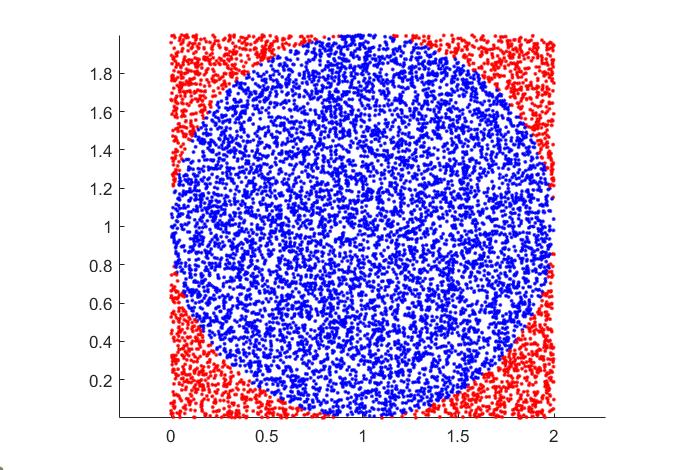
例题：使用蒙特卡洛法求圆周率

随机在正方形内抽取点，判断点落在圆内还圆外，通过面积公式比例求得圆周率

 

matlab代码如下

p=10000;%随机抽样个数
r=1;%半径
x0=1;
y0=1;%圆心坐标
n=0;%统计圆内的点数
hold on%持续在一张图内画点，没有该语句，图上只有一个点
for i=1:p
%rand函数产生（0，1）之间的的随机数
px=rand*2;
py=rand*2;%随机生成坐标
if(px-1)^2+(py-1)^2<1%判断是否在圆内
plot(px,py,".","Color","b");%在圆内在则在坐标上画蓝色的点
n=n+1;%统计在圆内的点数
else
plot(px,py,".","Color","r");%在圆外则画红色的点
end
end
axis equal%将横轴纵轴的定标系数设成相同值
s=(n/p)*4;
pi0=s;%pi在matlab中默认是圆周率的值，所以使用pi0代替

 

 

 上述例子符合随机均匀分布，可能会出现正态分布或者泊松分布，具体问题具体分析。