光栅图形学算法——直线扫描转换算法

文章和随笔都是自己学习过程中的笔记，如有错误，请多多包涵并指出，感激不尽

 

 

---

 

直线是最基本的图形，画直线的算法决定着图形的显示速度和质量。

计算机使用有限的像素点描绘出直线，但直线中包含有无限的点。

为了使计算机中离散的像素点逼近所画的直线，已知像素点的坐标为p（x，y）

所画直线的直线方程为y=kx+b，经过p₁（x₁，y₁），p₂（x₂，y₂）两点

得出k=  ( x₁ - x₂ ) / ( y₁ - y₂ )

已知p₁（x₁，y₁），

取整：x=x+1，y=k（x+1）+b，可以加上0.5后再抹去小数点后的数（四舍五入）

例如（1.7，0.8）→（2.2，1.3）→（2，1）

下面介绍三种基础算法

1. 数值微分法
2. 中点画线法
3. Bresenham算法

 

---

 

数值微分法（DDA）

直线初始点为p₁（x₁，y₁），y_i=kx_i+b

（x_i，y_i）下一个点横坐标为x_i+1=x_i+1，

得出   y_i+1 = k（ x_i + 1 ）+b

再得出   y_i+1 =y_i +k

得出k为增量

结论：当前坐标的纵坐标（y）是前一个纵坐标加上斜率k。使一个乘法和加法的运算变成一个加法

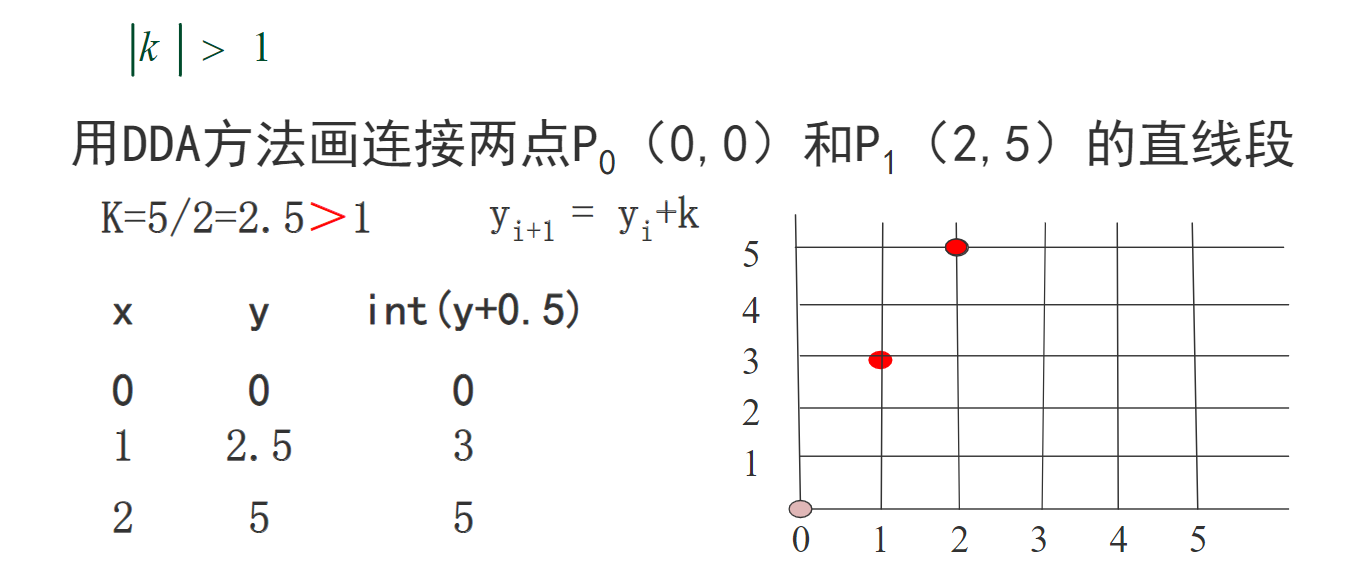
局限性：当 |k| >1时，x+1，y的增量过大，直线之间点的空袭太大，画不出来直线。

例如：光栅点太稀的情况，以下直线只用了三个点表示，这远远不能表示该直线。

 

---

 

中点画线法

 对数值微分法（DDA）进行改进

尽量使用整型 (int) 计算代替浮点型 (float) 运算。

使用一般式表示直线：

F（x，y）=0

Ax+By+C=0；

其中A = -(Δy) ，B = (Δx) ，C= -B(Δx)。

对于直线上方的点：F（x，y）>0

对于直线上的点：F（x，y）=0

对于直线下方的点：F（x，y）<0

 

每次向最大位移方向+1，另一个方向经过判断后选择是否+1。

例如：0< |k| <1，说明最大位移方向为x

则每次x+1，y需要判断是否需要+1

 

 

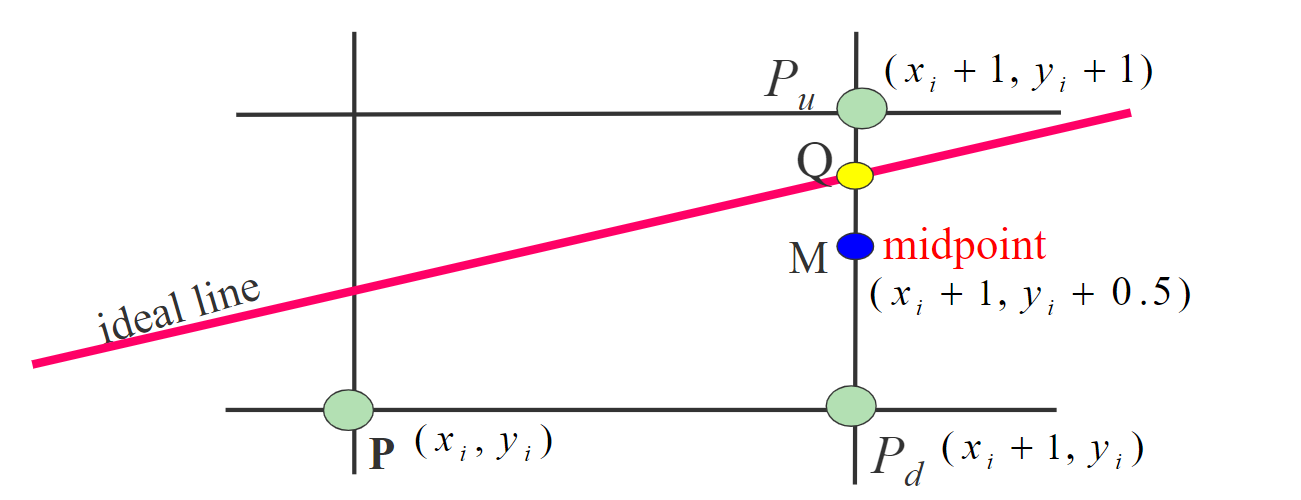
当中点M在交点Q下方时，取点P_u，即y_i+1=y_i+1

当中点M在交点Q上方时，取点P_d，即y_i+1=y_i

 

若 |k| >1，说明最大位移方向为y

则每次y+1，x需要判断是否需要+1（不作详细说明，与上例类似，只不过x，y交换）

 

如何判断Q在M上方还是下方呢？

将M（x_i+1，y_i+0.5）点代入F（x，y）中，代入Ax+By+C。

得到  d_i=F（x_i+1，y_i+0.5），即d_i=A( x_i+1 )+B( y_i+0.5 )+C

若 d_i<0，则说明中点M在交点Q下方，取点P_u，即y_i+1=y_i+1

若 d_i>0，则说明中点M在交点Q上方，取点P_d，即y_i+1=y_i

以上方法需要计算d_i，用到两次乘法，四次加法。

 

使用增量的思想，提高运算效率。

当0< |k| <1时，

直线的第一个像素点为p₀（x₀，y₀）则初始 d₀ 为

d₀ =F( x₀+1，y₀+0.5）

即d₀=A( x₀+1 )+B( y₀+0.5 )+C

　　=( Ax₀+By₀+C )+ (A+0.5B)

因为p₀（x₀，y₀）在直线上，所以 Ax₀+By₀+C =0

所以 d₀=A+0.5B

由上述中的

若 d_i<0，则说明中点M在交点Q下方，取点P_u，即y_i+1=y_i+1

 

若 d_i>0，则说明中点M在交点Q上方，取点P_d，即y_i+1=y_i

得出

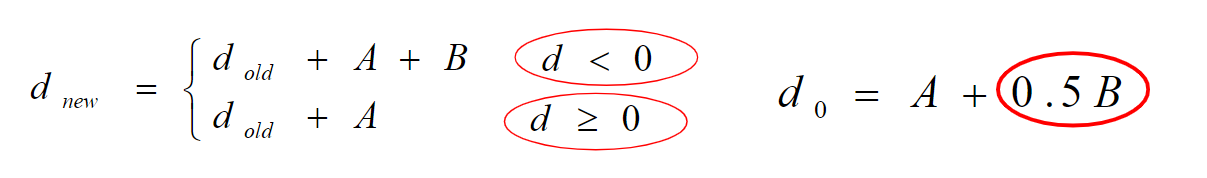
可用使用2d（反正也只需要判断d的正负）来计算，避免浮点型的运算。

 

解释：因为一定存在x=x+1，所以不论 d_i 的值为多少，d_i+1都会在 d_i 的基础上+A，

　　    然后判断d_i的正负，若 d_i>0，说明y_i+1=y_i，即d_i+1不需要在 d_i 的基础上+B；若 d_i<0，说明y_i+1=y_i+1，即需要+B。

 

---

 

 

Bresenham算法

 扩大算法的使用范围，使其不仅能应用在直线上，抛物线，圆等曲线也能应用。

 

将每行每列的像素点使用网格线连接，按照直线起点到终点的顺序，计算直线与垂直网格线的交点，确定与此交点最近的像素点。

 

当 0<|k| <1时

假设每次x+1，y的递增（减）量为0或者1，它取决于实际直线与最近像素点的距离，这个距离的最大误差是0.5。

设误差项d的初值为0，即d₀=0

d_i+1= d_i +k

若d_i+1>=1，则 d_i+1= d_i+1 - 1（保证d的相对性，只针对当前点，且在0，1之间）

 

 

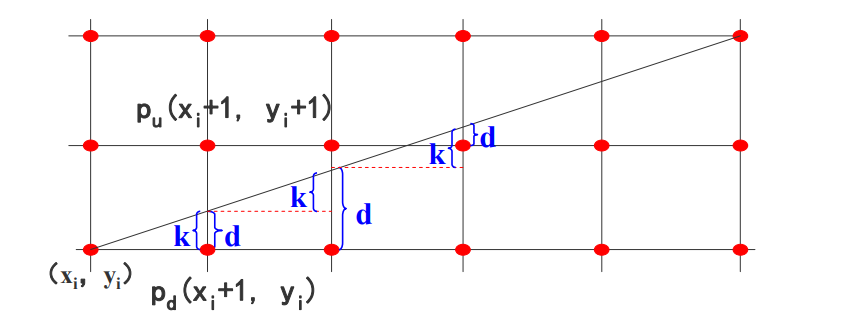
得到  x_i+1=x_i+1

若d>0.5，y_i+1=y_i+1

若d<0.5，y_i+1=y_i

若d=0.5，任选一个。

 

提高算法效率，使其变成整数加法。

1 . 令e= d -0.5

得到 x_i+1=x_i+1

若e>0，y_i+1=y_i+1

若e<0，y_i+1=y_i

若e=0，任选一个。

改进后不关心d的大小，只关心e的正负。

即 e₀= -0.5

e_i+1= e_i +k（若e_i+1> 0.5，则e_i+1= e_i+1 -1，理由同上）

k = dy / dx

2. 令D=2dx e

则D₀= -dx 

D_i+1=2dx e_i+1 

　　=2dx (e_i +k）

　　=2dx (e_i +dy / dx ）

　　=2dx e_i +2dy

因为D_i=2dx e_i，所以

D_i+1=D_i +2dy

当 D_i+1> dx时，D_i+1= 2dx e_i+1= 2dx( e_i+1 -1 )=D_i+1 -2dx

即 D_i+1=D_i+1 -2dx

算法步骤为：

1.输入直线的两端点P₀(x₀,y₀)和P1(x₁,y₁)。

2.计算初始值dx、dy、D= -dx、x=x₀、y=y_0。

3.绘制点(x,y)。

4.D更新为D+2dy。若D>dx，则将D更新为D-2dx，然后判断D的符号，若D>0，则(x , y)更新为 ( x+1,y+1)，否则 ( x ,y)更新为 (x+1 , y)。

5.当直线没有画完时，重复步骤3和4。否则结束。