【LeetCode】——分割回文串II
继续与动态规划斗智斗勇。。。
132. 分割回文串 II - 力扣(LeetCode) (leetcode-cn.com)
分析:记f[i]表示将字符串s[0:i]分割的最小次数。我们需要将列举出在[0:i]内的最大回文串数。我们可以列举出最后一个回文串s[j+1:i],那么f[i]就可以写出:
f[i]=min(f[j])+1;
我们还要再考虑一种情况:s[0:i]是一个回文串,此时不需要任何分割,即f[i]=0。
那么,问题就转到了如何确定s[0:i]中的回文串数目。我们可以再用一次动态规划来解决这个问题:
设g[i][j]表示s[i:j]是否为回文串,那么其状态转移方程为:
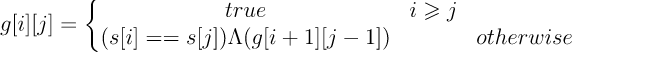
class Solution {
public:
int minCut(string s) {
int n=s.length();
vector<vector<bool>> g(n,vector<bool>(n,true));
for(int i=n-1;i>=0;i--){
for(int j=i+1;j<n;j++){
g[i][j]=(s[i]==s[j])&&g[i+1][j-1];
}
}
vector<int> f(n,INT_MAX);
for(int i=0;i<n;i++){
if(g[0][i]){
f[i]=0;
}
else{
for(int j=0;j<i;++j){
if(g[j+1][i]){
f[i]=min(f[i],f[j]+1);
}
}
}
}
return f[n-1];
}
};代码中还有一些细节值得我们注意:
比如这里:

为什么我们需要从后往前遍历?我刚开始写的时候是从前往后的,跑不通。仔细想想才发现,我们需要用到后一行的状态信息g[i+1][j-1],如果从前往后遍历的话,g[i+1][j-1]是未更新过的初始化量true,那么就存在一种可能:s[i]==s[j],但s[i+1,j-1]不是回文串,g[i+1][j-1]此时却为true,导致最终结果有误。所以在动态规划问题中遍历方向一定要看我们需要用到之前的状态还是之后的状态,如果是之前的我们就可以从前往后遍历,如果要用到后一行的状态那么我们就需要从后往前遍历,这一点在背包问题的状态压缩写法中也有所体现。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号